Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Ключевое слово: |
|
| Page views: 14972 |
Print version Full issue in PDF (1.53Mb) |
Среди задач, встающих при разработке информационных систем моделирования и поддержки принятия решений, класс задач многокритериальной оптимизации (МКО) является одним из наиболее сложных. Это связано с тем, что оптимальное решение х* задачи МКО, в общем случае не являясь оптимальным ни для одного из частных критериев, должно быть компромиссным (в определенном смысле) для векторного критерия в целом; при этом оценка качества получено- го решения является субъективной и зависит от предпочтений лица, принимающего решения (ЛПР). Рассмотрим задачу оптимизации комплекса технико-экономических показателей взрывных работ на уступе карьера при подготовке горных пород к выемке. В результате анализа предметной области взрывных работ на карьере были выявлены следующие технико-экономические показатели, в наибольшей степени влияющие на качество производства взрыва: 1) степень дробления зависит от длины заряда в скважине – lзар, расстояния между скважинами в ряду – a и между рядами скважин – b; 2) ширина развала горной массы после взрыва зависит от длины заряда в скважине – lзар, расстояния между скважинами в ряду – a и между рядами скважин – b, от величины интервала замедления – t; 3) расстояние безопасного удаления для объектов зависит от длины заряда в скважине – lзар, расстояния между скважинами в ряду – a. Для каждого технико-экономического показателя на основании формул, содержащихся в типовом проекте буровзрывных работ, были построены математические модели, включающие формулы расчета значений каждого из показателей и системы ограничений, накладываемые на эти значения. Формулы в построенных моделях являются мультимодальными непрерывными функциями от многих аргументов. Для оценки результатов решений на моделях технико-экономических показателей введены следующие критерии оптимальности. Критерий оптимальности для оценки степени дробления горных пород Yε представим математически в следующем виде:
где ε – подвергаемая оценке степень дробления горной породы; ε* – оптимальная степень дробления горной породы. Критерий оптимальности для оценки ширины развала горной массы YB после взрыва имеет следующую математическую запись:
где B – подвергаемая оценке ширина развала горной массы; ξB – коэффициент, определяемый по формуле:
где Bmin – минимально допустимая ширина развала горной массы, определяемая используемым оборудованием. Критерий оптимальности для оценки расстояний безопасного удаления YR представим следующим видом:
где R – подвергаемое оценке безопасное расстояние; ξR – коэффициент, определяемый по формуле:
где Rmax – максимально допустимое безопасное расстояние. Рассмотрим некоторое пространство решений W, определенное на четырехмерном линейном пространстве действительных чисел R4:
Пусть на W наложены некоторые ограничения в виде областей Ωa, Ωb, Ωlзар и Ωτ допустимых значений a, b, lзар и τ:
Тогда с учетом (6) и (7) множество допустимых решений X может быть записано в виде:
Совокупность критериев Y, характеризующих качество решения Xq, является трехмерным вектором, определенным в трехмерном линейном пространстве вещественных чисел R3, и связь между решениями и значениями критериев устанавливается отображением f, действующим из пространства решений W в критериальное пространство R3, то есть
Таким образом, множество достижимости Y в критериальном пространстве R3 может быть задано следующим образом:
Предпочтения ЛПР в критериальном пространстве задаются бинарным отношением строгого порядка:
Решаемая математическая задача обладает следующими особенностями: - множества аргументов критериальных функций частично пересекаются, то есть сложность задачи состоит в том, что при изменении значения конкретного аргумента для оптимизации решения по одному из критериев значения других критериев также изменяются по неявной зависимости; - анализу подвергаются критерии, выраженные математическими функциями и формирующие невыпуклые множества достижимых целей; - функции критериев задачи не отвечают условиям унимодальности, что не позволяет использовать для их анализа хорошо разработанные градиентные методы оптимизации. Выбор метода МКО технико-экономических показателей взрывных работ на карьере Поскольку с математической точки зрения все точки паретовой границы равноценны, в многокритериальных методах поддержки принятия решений центральное место играет ЛПР, на основе предпочтений которого в зависимости от задачи отбирается единственное эффективное решение. К настоящему моменту разработано несколько тысяч различных многокритериальных методов. Классифицируем методы принятия решений по роли ЛПР: методы без участия ЛПР; методы, использующие ЛПР для построения решающего правила; итеративные человеко-машинные методы; итеративные методы, основанные на визуализации паретовой границы. Методы первых двух групп часто называют методами сведения многокритериальных задач к однокритериальным. Отличие первой группы от второй состоит в том, что в первой группе методов решающее правило строится без участия ЛПР на основе аксиоматики или некоторых эвристических принципов, а во втором случае используется информация о предпочтениях ЛПР. Поскольку в реальной жизни решение принимается человеком или группой лиц, которые несут ответственность за его последствия, такие методы не нашли широкого применения. Методы без участия ЛПР могут применяться в системах, время выработки управляющих воздействий в которых является критичным, например, в системах операторского контроля и управления (SCADA), но непригодны для использования на более высоких уровнях, так как эти методы оперируют только одним критерием и полностью исключают участие ЛПР в процессе принятия решения. Главными недостатками методов, использующих ЛПР для построения решающего правила, является невозможность их применения к нелинейным мультимодальным функциям, малое участие ЛПР в процессе решения задач и при этом отсутствие у ЛПР права на ошибку. Итеративные человеко-машинные методы основаны на итерациях, в которых перемежаются действия человека и расчет по некоторой компьютерной программе, решающей вспомогательную задачу оптимизации. Действия человека состоят в том, что он изучает результаты решения задачи оптимизации и высказывает свои предпочтения и представления о параметрах задачи оптимизации, решаемой на следующей итерации, затем компьютер решает очередную вспомогательную задачу оптимизации. Многокритериальную информацию все чаще представляют с использованием современных компьютерных средств. Развитием итеративных человеко-машинных методов стали итеративные методы, основанные на визуализации паретовой границы, ориентированные на итеративный процесс принятия решений в форме диалога с пользователем, организуемого с помощью средств мультимедиа. Такие методы наиболее рационально применять для решения многокритериальных задач MES-уровня, в которых математический аппарат должен сочетаться с удобным и информативным графическим человеко-машинным интерфейсом. Представим сравнительную характеристику итеративных методов, основанных на визуализации паретовой границы (табл. 1). С точки зрения решаемой задачи наиболее важными являются удобство использования метода при трех критериях и простота его применения. Из таблицы 1 видно, что в наибольшей степени удовлетворяющим принятым критериям оценки методов является метод достижимых целей (МДЦ). Тем не менее этот метод обладает двумя недостатками: наиболее выигрышным случаем применения классического МДЦ является решения задач МКО с фиксированным количеством стратегий, кроме того, метод крайне субъективен. Таблица 1
Проблему субъективности МДЦ можно решить путем разработки сценария принятия решения, основанной на нахождении оптимального решения в ограничениях, выявленных в диалоге с ЛПР с помощью МДЦ. Касательно другого недостатка, наиболее выигрышным случаем применения классического МДЦ является решение задач МКО с фиксированным количеством стратегий (вариантов решений), в которых возможно или представление ЛПР всего множества достижимых целей, или, по крайней мере, множество достижимых целей может быть получено перебором всех решений. В рассматриваемой задаче анализу подвергаются критерии, выраженные математическими нелинейными мультимодальными функциями, и количество возможных вариантов решений стремится к бесконечности. Это затрудняет фазу построения множества достижимых целей. Для уменьшения числа рассматриваемых ЛПР вариантов решения необходимо сформулировать правила построения репрезентативной выборки значений каждого из критериев, а также число формируемых областей карты решений для пары других критериев. Для этого разработан комплексный метод нелинейной оптимизации мультимодальных функций от многих переменных. В таблице 2 представлена сравнительная характеристика методов нелинейной оптимизации мультимодальных функций. Из нее видно, что ни один метод не удовлетворяет в полной мере поставленным требованиям. При этом объединение методов случайного поиска с градиентными методами приводит к формированию комплексного метода, удовлетворяющего всем требованиям исследования. Таблица 2
Комплексный метод нелинейной оптимизации мультимодальной функции состоит в следующем. На первом шаге выполняется разбиение анализируемой функции на области гиперплоскостей. Для каждого аргумента функции методом Монте-Карло формируется подмножество его значений. Количество разбиений определяется среднеквадратическим отклонением для конкретной критериальной функции. При переходе в критериальное пространство в совокупности эти множества образуют множества гиперплоскостей. Полученные области рассматриваются как выпуклые. В каждой из полученных областей гиперплоскостей с помощью градиентного метода находится минимум. Для нахождения минимума по области гиперплоскости используется градиентный метод скорейшего спуска с определением шага по правилу Армихо. Далее полученное множество минимумов по областям гиперплоскостей сортируется, и из него выбирается минимальное значение. Содержательное описание модернизированного МДЦ На первой стадии решения строятся карты решений МДЦ для каждого из критериев. В качестве стратегий используются классы целей, выявляемые путем анализа функции третьего критерия. При формировании множества достижимых целей сначала выполняется разбиение функции анализируемого критерия на гиперплоскости. Для каждого параметра производства взрыва одним из методов Монте-Карло формируется подмножество его значений. Количество разбиений определяется среднеквадратическим отклонением для конкретного критерия. При переходе в критериальное пространство в совокупности эти множества образуют множества гиперплоскостей. Полученные гиперплоскости рассматриваются как выпуклые. В каждой из полученных гиперплоскостей с помощью градиентного метода находится минимум. Далее полученное множество минимумов по гиперплоскостям сортируется, и его элементы объединяются в классы целей. Количество классов также определяется среднеквадратическим отклонением по данному критерию, то есть при коэффициенте функции среднеквадратического отклонения, равном 1/15, данный критерий будет разбит на 15 классов. После этого для каждого класса целей строится область множества достижимых целей для двух других критериев. Наложение друг на друга областей, соответствующих различным классам целей, образует карту решений. Для уменьшения субъективизма МДЦ применяется сценарий ограничения субъективного участия ЛПР в процессе принятия решения. Рассмотрим сценарий ограничения субъективного участия ЛПР в процессе принятия решения. Его схема представлена на рисунке. После того как карты решений МДЦ построены, ЛПР может решать задачу тремя способами. Первый из них основывается на стандартных механизмах МДЦ: ЛПР с помощью визуального анализа по карте решений интерактивно выбирает рациональную критериальную точку. Второй способ заключается в сведении задачи к однокритериальной. Для этого от ЛПР требуется задать основной критерий, после чего задача решается методом основного критерия. Наконец, ЛПР может использовать механизм поддержки принятия решений, заключающийся в следующем. Задача решается методом уступок. На каждой итерации ЛПР в визуальной форме на карте решений задает уступки для текущего критерия, что позволяет избежать основного недостатка метода уступок – отсутствие наглядности. Другой его недостаток – отсутствие адаптации к анализу критериев, представленных мультимодальными нелинейными функциями, – устраняется счет применения комплексного метода нелинейной оптимизации мультимодальной функции. Процесс выработки решения заканчивается при переборе всех критериев.
риальной оптимизации. Для исследования взаимного влияния технико-экономических показателей производства взрывного разрушения горных пород на карьере друг на друга, а также выявления их совокупного влияния на качество взрыва осуществлено развитие МДЦ на случай непрерывных шкал критериев. Для пошагового анализа функции от многих переменных разработан и использован комплекс методов, включающий разбиение множества решений методом Монте-Карло на интервалы с последующим применением градиентного метода скорейшего спуска. По сравнению с классическим, модернизированный МДЦ обладает следующими преимуществами: - анализу подвергаются модели с непрерывными шкалами критериев, выраженных неунимодальными функциями, формирующими невыпуклые множества достижимых целей; - при зондировании пространства решений за счет применения градиентного метода происходит более жесткий отбор интересующих ЛПР точек; - наблюдается снижение количества экспериментальных точек во множестве достижимых целей; - разработан сценарий ограничения субъективного участия ЛПР в процессе решения задачи. Предложенный алгоритм может применяться для решения широкого спектра многокритериальных задач. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Permanent link: http://swsys.ru/index.php?id=408&lang=en&page=article |
Print version Full issue in PDF (1.53Mb) |
| The article was published in issue no. № 1, 2007 |
Perhaps, you might be interested in the following articles of similar topics:
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Эвристические и точные методы программной конвейеризации циклов
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Формулировка задачи планирования линейных и циклических участков кода
Back to the list of articles
 , (1)
, (1) , (2)
, (2) , (3)
, (3) , (4)
, (4)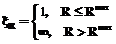 , (5)
, (5) (6)
(6) . (7)
. (7) (8)
(8) . (9)
. (9) (10)
(10) . (11)
. (11)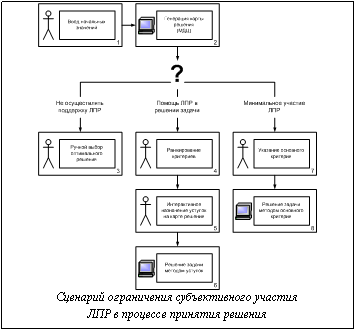 На основе изложенного сделаем следующие выводы. В статье на примере оптимизации технико-экономических показателей взрывных работ на карьере рассмотрен один из возможных вариантов построения процесса принятия многокритериальных решений. В процессе исследований был проведен анализ существующих методов многокрите-
На основе изложенного сделаем следующие выводы. В статье на примере оптимизации технико-экономических показателей взрывных работ на карьере рассмотрен один из возможных вариантов построения процесса принятия многокритериальных решений. В процессе исследований был проведен анализ существующих методов многокрите-