Совершенствование методов исследований в молекулярной биологии и генетике привело к лавинному нарастанию объемов экспериментальных данных. Благодаря этому все более востребованными становятся производительные компьютерные технологии, предназначенные для автоматизации анализа, хранения и преобразования резуль- татов, полученных в лабораториях, что, в свою очередь, дает импульс научной деятельности в области биоинформатики [1].
Несмотря на молодость этой науки, а биоинформатика появилась в 1970-х годах, в ней уже сформировались некоторые традиционные направления исследований, такие как анализ ДНК и РНК, распознавание функциональных сайтов, реверс-моделирование пространственных структур биополимеров и т.п.
 Одной из наиболее важных задач является разработка алгоритмов распознавания сайтов связывания с транскрипционными факторами (ССТФ) (см., например [2]). Как известно, синтез нового белка в клетке начинается с процесса транскрипции, то есть считывания информации ДНК с помощью РНК-полимеразы (см. рисунок). Фермент РНК-полимераза определяет начало необходимого участка ДНК, присоединяется к нему и производит считывание РНК. РНК-полимераза не может присоединиться к ДНК без участия транскрипционных факторов, специфических белков, которые формируют место для посадки РНК-полимеразы. Эти белки прикрепляются к специфичным участкам – ССТФ. Различные белки присоединяются к различным по набору нуклеотидов участкам ДНК.
Одной из наиболее важных задач является разработка алгоритмов распознавания сайтов связывания с транскрипционными факторами (ССТФ) (см., например [2]). Как известно, синтез нового белка в клетке начинается с процесса транскрипции, то есть считывания информации ДНК с помощью РНК-полимеразы (см. рисунок). Фермент РНК-полимераза определяет начало необходимого участка ДНК, присоединяется к нему и производит считывание РНК. РНК-полимераза не может присоединиться к ДНК без участия транскрипционных факторов, специфических белков, которые формируют место для посадки РНК-полимеразы. Эти белки прикрепляются к специфичным участкам – ССТФ. Различные белки присоединяются к различным по набору нуклеотидов участкам ДНК.
На сегодня разработано порядка 100 алгоритмов распознавания ССТФ. Такие алгоритмы используют нейронные сети [3], различные статистические модели [4], основаны на оценке физико-химических свойств [5], на использовании олигонуклеотидных матриц [6], весовых матриц [7] и др., а также учитывают комбинации ССТФ, контекст и/или гомологичные последовательности других организмов [8]. Однако невозможно выделить какой-либо алгоритм в качестве лидера. Все существующие алгоритмы имеют как свои дос- тоинства, так и недостатки или ограничения, а качество распознанных данных очень низкого уровня [9].
Существует несколько моделей, используемых для поиска сайтов связывания белков с ДНК, наиболее распространенными среди них являются представление в виде консенсуса (регулярного выражения) и в виде позиционной весовой матрицы (ПВМ, PWM – position weight matrix) [4]. Консенсус имеет вид слова, составленного из нуклеотидов, наиболее часто встречающихся на соответствующих позициях сайта (табл. 1). На каждой по- зиции консенсусной последовательности стоит буква, которая наиболее часто встречается в соответствующей позиции сайта. Если часто встречаются две или более букв, то применяется буква, вы- бранная согласно определенному коду. Позиции, не имеющие фиксированного нуклеотида, обозначают вырожденным символом в соответствии с нормами IUPAC. Консенсусы хорошо подходят для описания консервативных (редко меняющихся) последовательностей сайтов связывания факторов транскрипции.

Однако для варьирующихся последовательностей консенсусы недостаточно функциональны. ПВМ, которые впервые были введены для характеристики сайтов инициации транскрипции и трансляции у E.coli (кишечная палочка), гораздо лучше подходят для описания сайтов связывания факторов транскрипции и способны количественно охарактеризовать частые и редкие вариации в последовательности сайтов.

Позиционная весовая матрица представляет собой матрицу размера 4×L, где L – длина сайта, а номер столбца соответствует позиции нуклеотида в сайте. В таблице 2 по горизонтали расположены позиции в сайте связывания с ТФ, а по вертикали количество букв, встретившихся в соответствующей позиции в экспериментально известных сайтах. Например, в группе экспериментальных сайтов в первой позиции шести сайтов встретилась буква А, в одном сайте буква С, в одном – буква G и в одном – буква T. В каждой ячейке матрицы хранится частота встречаемости j-го нуклеотида на i-й позиции. Вес, порождаемый матрицей при выравнивании с некоторым участком последовательности, обычно вычисляется как сумма элементов матрицы, соответствующих нуклеотидам, стоящим в каждой позиции рассматриваемого участка. Для удобства полученное значение нормируют на отре- зок [0, 1] следующим образом: 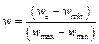 , где wmin и wmax – минимальный и максимальный вес последовательности соответственно.
, где wmin и wmax – минимальный и максимальный вес последовательности соответственно.
Таким образом, ПВМ предоставляет достаточно полное описание участка ДНК, с которым способен связываться конкретный белок, и может быть применена при сканировании геномной последовательности для поиска сайтов, дающих достаточно хороший вес w, приблизительно соответствующий вероятности связывания белка с последовательностью. Использование ПВМ позволяет достаточно эффективно предсказывать сайты связывания белков. Однако следует отметить, что у весовых матриц есть свои недостатки. Одним из них является то, что стандартная ПВМ не учитывает взаимное влияние соседних позиций сайта, однако наличие таких зависимостей было показано для некоторых факторов [10].
Авторы данного исследования разработали метод поиска статистически перепредставленных пар сайтов связывания, из которых одна матрица является фиксированной, а другая может варьироваться. Пользователь может задать длину окна, в которое должны попадать пары сайтов, ориентацию сайтов, а также направление последовательностей. Для каждой пары матриц программа вычисляет частоту встречаемости, p-value, и долю ложных отклонений гипотез (FDR, False Discovery Rate). Одной из матриц в паре будет выступать фиксированная наперед заданная матрица, другой матрицей будет каждая матрица из профиля, заданного пользователем. Данный метод включает в себя использование алгоритма match для распознавания ССТФ с помощью весовых матриц, распространяемого компанией Biobase.
Алгоритмы
Опишем общую идею алгоритма.
Для каждой фиксированной позиции p рассмотрим все сайты связывания, распознанные на отрезке [p, p+win], где win – заданный размер окна. Для очередного найденного сайта Sk=(xk, Mk) можно рассчитать число пар данного сайта с остальными сайтами, попавшими в рассматриваемый отрезок. Таким образом, сформируем таблицу Tk:
|
Matrix-1
|
Matrix-2
|
Matrix-3
|
Matrix-4
|
…
|
Matrix-Nm
|
|
Count-1
|
Count-2
|
Count-3
|
Count-4
|
…
|
Count-Nm
|
Для очередного распознанного сайта корректируем значения следующим образом.
1. Вычитаем из таблицы сайты, которые выпали после сдвига окна, то есть вычитаем все Sj, такие, что xj ≤ xk –1, если xk > xk-1.
2. Добавляем к значениям таблицы те распознанные сайты связывания, которые попали в рассматриваемое окно после сдвига.
3. Заполняем результирующую таблицу T путем добавления значений из таблицы Tk.
4. Переходим к следующему сайту.
Далее на основании полученной таблицы T и фоновых данных подсчитаем статистику для всех пар матриц, которые подходят заданным входным параметрам. Для каждой такой пары матриц вычисляем следующие параметры.
· Средняя частота встречаемости пары
F(Mk, Ml) = T(Mk, Ml) * 1000 / LS,
где 
· Средняя фоновая частота встречаемости пары Fe(Mk, Ml) = M × PF(Mk, Ml) × win / win0, где win0 – размер окна, с которым вычислены фоновые данные; PF(Mk, Ml) – частота встречаемости пары матриц в фоновом наборе данных; M – понижающий множитель, значение которого зависит от входных данных. Значение М тем меньше, чем сильнее фиксируется модель распознавания. Например, для самого общего случая, когда рассматривается модель с учетом любой позиции фиксированной матрицы и учитываются все направления (модель **), М = 1. В то же время, если установить конкретную позицию фиксированной матрицы (например, фиксированная матрица должна стоять первой в паре), М примет значение ½. Также, если зафиксировать какое-либо направление (например модель >*), получим М = 3/8 и так далее.
· Значение  ,
,
где 

· P-значение p = 2×Ф(S), где Ф – функция стандартного нормального распределения.
В случае сильного перепредставления сайтов фиксированной весовой матрицы в фоновом наборе последовательностей рекомендуем вычислять восстановленное P-значение: p = 2×Ф(Scorr), где 


Здесь LM1 – длина сайта фиксированной матрицы; N1 – количество распознанных сайтов фиксированной матрицы; SF(Mk) – количество распознанных сайтов матрицы Mk в фоновом наборе последовательностей.
· FDR (false discovery rate) – отношение ошибочно распознанных пар сайтов к общему числу распознанных пар сайтов. Если pval – набор P-значений, упорядоченных по возрастанию, pvalCount – количество элементов в массиве pval, то для каждого pvali найдем fdri следующим образом:

 Пример работы программы представлен в таблице 3. Найденные пары сайтов отсортированы в порядке возрастания p-value. Matrix1 – это фиксированная матрица; Matrix2 – варьирующая матрица; F – частота встречаемости данной пары в пользовательском наборе данных; F_corr – частота встречаемости пары в пользовательском наборе, скорректированная с учетом различия частот фиксированной матрицы в пользовательском наборе и в фоновом наборе последовательностей; Fe – фоновая частота пары, оцененная на основании фоновой выборки. Score – характеристика отличия частот в пользовательской и фоновой выборках с учетом дисперсии.
Пример работы программы представлен в таблице 3. Найденные пары сайтов отсортированы в порядке возрастания p-value. Matrix1 – это фиксированная матрица; Matrix2 – варьирующая матрица; F – частота встречаемости данной пары в пользовательском наборе данных; F_corr – частота встречаемости пары в пользовательском наборе, скорректированная с учетом различия частот фиксированной матрицы в пользовательском наборе и в фоновом наборе последовательностей; Fe – фоновая частота пары, оцененная на основании фоновой выборки. Score – характеристика отличия частот в пользовательской и фоновой выборках с учетом дисперсии.
 Для сравнения в таблице 4 представлены результаты, полученные без применения коррекции p-value. Для вычисления Score, в отличие от предыдущей таблицы, используется оригинальная частота пары сайтов F, которая сравнивается с Fe. Частота F не скорректирована, то есть не учитывает перепредставленность фиксированной матрицы V$AP1_Q6_02 в пользовательской выборке. Этот режим оценивает различие представленности данной пары по отношению к фоновой выборке.
Для сравнения в таблице 4 представлены результаты, полученные без применения коррекции p-value. Для вычисления Score, в отличие от предыдущей таблицы, используется оригинальная частота пары сайтов F, которая сравнивается с Fe. Частота F не скорректирована, то есть не учитывает перепредставленность фиксированной матрицы V$AP1_Q6_02 в пользовательской выборке. Этот режим оценивает различие представленности данной пары по отношению к фоновой выборке.
В обоих случаях зафиксирована весовая матрица V$VJUN_01. Анализ проводился на данных JUN ChIP из библиотеки Proteome. Коррекция P-значения включена, так как JUN ChIP области перенасыщены сайтами матрицы V$VJUN_01.
Выбор размера окна для анализа
Какой-либо стратегии выбора размера окна нет: пользователь может самостоятельно решить, какое окно использовать. По умолчанию используется окно win = 200 нуклеотидов. Тесты показали, что нет прямой зависимости расстояния между сайтами в паре и качеством распознанных результатов. Для исследования этого вопроса рассматривалась пара матриц Ets/AML на промоторах и в межгенных областях разной длины (1 000, 2 000, 11 000 нуклеотидов для каждого вида данных). Результаты показали случайное распределение расстояния между сайтами в паре.
Выбор пороговых значений для весовых матриц
Точный подбор пороговых значений для весовых матриц, возможно, имеет некоторое положи- тельное влияние на результат. Иными словами, некоторые пороговые значения лучше подходят для распознавания пар сайтов связывания.
Авторы предлагают использовать профиль vertebrate_non_redundant_minFN.prf, который минимизирует ошибку исключения верных результатов. Такой статистики достаточно для большинства весовых матриц. Если пользователь хочет использовать другой профиль, фоновая статистика также должна быть пересчитана с помощью алгоритма, представленного далее. Алгоритм получения фоновой статистики тоже встроен в разработанное авторами java-приложение.
Очевидно, что для некоторых матриц можно получить очень мало распознанных результатов, поэтому пользователю следует использовать достаточно большие наборы последовательностей, чтобы получить статистику по таким весовым матрицам.
Выбор фонового набора последовательностей
Количество сайтов в разных наборах после- довательностей различно для разных матриц. Некоторые сайты перепредставлены во всех регуля- торных областях, другие сайты равномерно распределены между промоторами и межгенными участками. Предлагаем использовать промоторные регионы в качестве фонового набора последовательностей. Таким образом, фиксируется область применения описываемого алгоритма только для регуляторных регионов, что хорошо соотносится с задачей распознавания регуляторных модулей. В то же время пользователь не ограничен каким-либо набором последовательностей и может выбрать любые данные для расчета фоновой статистики.
Получение файла фоновой статистики
Для получения корректного файла фоновой статистики требуется большое количество фоновых данных. Для расчета фоновой статистики требуется не менее 200 групп последовательностей с суммарной длиной 50 000 нуклеотидов в каждой группе. Файл фоновой статистики содержит три набора данных: частота встречаемости распознанных сайтов связывания, частота встречаемости и стандартное отклонение пар распознанных сайтов связывания для каждой пары весовых матриц. Обозначим группы последовательностей Gi, количество групп gCount, количество последовательностей в одной группе seq_in_group.
1. Разделим исходный набор на группы по seq_in_group последовательностей в каждой. Если в последнюю группу попало меньше, чем seq_in_group последовательностей, исключаем ее из дальнейших вычислений.
2. Для каждой группы Gi проводим поиск пар Pik,l (рассматриваются все направления матриц, все обходы последовательностей, а также позиции матриц в парах MkMl и MlMk).
3. Вычисляем частоты встречаемости распознанных сайтов связывания, частоты встречаемости и стандартные отклонения пар распознанных сайтов связывания.
4. Сохраняем статистику в файл в соответствии с форматом.
· Частота встречаемости сайтов связывания SF(Mk): 
 где Lk – длина матрицы; Mk, Nik – количество сай- тов связывания, распознанных матрицей Mk в группе Gi.
где Lk – длина матрицы; Mk, Nik – количество сай- тов связывания, распознанных матрицей Mk в группе Gi.
· Частота встречаемости пар сайтов связывания PF(Mk, Ml):


· Стандартное отклонение пар сайтов связывания PSD(Mk, Ml):



Comatch можно запускать в двух режимах: в стандартном и с коррекцией P-значения. В зависимости от этого пользователь получит разные P-значения и FDR. Пользователь сам решает, какой режим использовать. Авторы рекомендуют включать коррекцию P-значения в ситуациях, когда входной набор последовательностей сильно обогащен сайтами исследуемой фиксированной весовой матрицы. В этом случае исключается зависимость P-значения от перепредставленности фиксированной матрицы и можно утверждать, что получены значимые результаты для пар с P-значением до 0,05.
В ином случае (без использования коррекции P-значения) в результатах отразится общая перепредставленность каждой конкретной пары сайтов связывания по сравнению с другими парами в фоновой статистике. Имеет смысл использовать этот режим, если входные данные не перенасыщены сайтами фиксированной весовой матрицы.
В результате разработана программа, которая проводит поиск перепредставленных пар сайтов связывания в наборе последовательностей, причем одна из весовых матриц в паре фиксированная. Результатом ее работы является файл, в котором для каждой пары содержатся P-значения и значения FDR.
FDR определяет процент ложных результатов из тех результатов, которые имеют меньший или такой же FDR.
Результаты тестов (в том числе приведенного примера) показали, что разработанный алгоритм верно предсказывает пары вероятных сайтов связывания, активируемых совместно, находит значимые статистические различия по сравнению с фоновыми значениями.
Работа выполнена по заказу компании Biobase GmbH с использованием БД Transfac.
Литература
1. Schattner P1. Genomics made easier: an introductory tutorial to genome datamining. Genomics, 2009, vol. 93, no. 3, pp. 187–95.
2. Hannenhalli S1. Eukaryotic transcription factor binding sites--modeling and integrative search methods. Bioinformatics, 2008, vol. 24, no. 11, pp. 1325–1331.
3. Liu D., Xiong X., DasGupta B., Zhang H. Motif discoveries in unaligned molecular sequences using self-organizing neural network. IEEE Transactions on Neural Networks, 2006, vol. 17, pp. 919–928.
4. Down T.A., Hubbard T.J.P. NestedMICA: sensitive inference of over-represented motifs in nucleic acid sequence. Nucleic Acids Research, 2005, vol. 33, pp. 1445–1453.
5. Djordjevic M., Sengupta A.M., and Shraiman B.I. A biophysical approach to transcription factor binding site discovery. Genome Res., 2003, vol. 13, no. 11, pp. 2381–2390.
6. Liang S. cWINNOWER algorithm for finding fuzzy DNA motifs. IEEE Computer Society Bioinformatics Conf., 2003, pp. 260–265.
7. Kel A.E., Gobling E., Reuter I., Cheremushkin E., Kel-Margoulis O.V. and Wingender E. MATCH: a tool for searching transcription factor binding sites in DNA sequences. Nucleic Acids Research, 2003, vol. 31, no. 13, pp. 3576–3579.
8. Carmack C.S., McCue L.A., Newberg L.A., Lawrence C.E. PhyloScan: identification of transcription factor binding sites using cross-species evidence. Algorithms for Molecular Biology, 2007, vol. 2, p. 1.
9. Modan K. Das and Ho-Kwok Dai. A survey of DNA motif finding algorithms. BMC Bioinformatics, 2007, vol. 8 (suppl 7), p. 21.
10. Zhou Q., Liu J.S. Modeling within-motif dependence for transcription factor binding site predictions. Bioinformatics, 2004, vol. 20, no. 6, pp. 909–916.



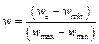 , где wmin и wmax – минимальный и максимальный вес последовательности соответственно.
, где wmin и wmax – минимальный и максимальный вес последовательности соответственно.
 ,
,








 где Lk – длина матрицы; Mk, Nik – количество сай- тов связывания, распознанных матрицей Mk в группе Gi.
где Lk – длина матрицы; Mk, Nik – количество сай- тов связывания, распознанных матрицей Mk в группе Gi.




