Модель Bag-of-words («набор слов») – самая популярная и простая модель представления текста, применяемая во многих задачах Text Mining [1, 2]. Модель представляет текст как набор слов без учета их взаимного расположения и взаимных связей. При ее использовании семантическая близость двух текстов (двух наборов слов) оценивается по количеству совпадающих слов. Это означает, что два текста, в которых мало общих слов или вообще нет, считаются семантически и тематически неблизкими. Игнорирование семантических связей между словами – главный недостаток модели Bag-of-words. Другой ее важный недостаток в том, что тексты как наборы слов проецируются в пространство высокой размерности и высокой разрежен- ности, что обусловлено объемом используемого словаря. Как результат, возникает феномен «проклятия размерности», характеризующийся экспоненциальным ростом сложности вычислений из-за увеличения размерности данных. По этой причине модель Bag-of-words часто комбинируется с техниками редукции признакового пространства [3].
На преодоление недостатков модели Bag-of-words в последние годы направлено множество ис- следований. Большинство из них фокусируются на способах перехода от традиционного представления текстов в разреженном и зашумленном пространстве Bag-of-words к представлению в новых, семантически более богатых пространствах, в которых алгоритмы машинного обучения достигали бы лучших результатов [4]. Это означает, что так или иначе, но все эти исследования манипулируют наборами семантически связанных слов, разница только в подходах к выбору и формированию этих наборов.
Среди существующих подходов можно выделить три основных класса работ. Первый класс работ объединяет подходы, формирующие наборы семантически связанных слов на основе концептов, второй – на основе контекстных векторов, третий – на основе латентных семантических связей.
Подход, используемый в данной работе, можно отнести ко второму классу. Авторы придерживаются точно такой же стратегии обогащения представлений текста семантическими связями, как в модели контекстных векторов: то есть строится матрица семантических связей, которая использу- ется как оператор, отображающий тексты из про- странства Bag-of-words в пространство контекстных векторов. Вклад данной работы заключается в новом способе построения и использования матрицы семантических связей. Предлагается трехэтапная процедура извлечения самых устойчивых и значимых связей, которые ее формируют.
Конечной целью работы является доказательство превосходства построенной модели по сравнению с моделью Bag-of-words при выполнении бинарной классификации текстов. Для сравнения этих двух моделей была реализована серия экспериментов на стандартной коллекции Reuters 21578. Результаты экспериментов демонстрируют улучшение качества классификации текстов по сравнению с известными методами.
Состояние проблемы и текущие исследования
Подходы на основе модели концептов. В числе популярных расширений модели Bag-of-words, позволяющих учитывать семантические связи, модель Bag-of-concepts и ее вариации [5–9]. Модель описывает представления текстов с помощью концептов, которые трактуются как категории, объединяющие семантически связанные слова. В работе [10] отмечается, что концепты как дескрипторы обладают тремя важнейшими преимуществами по сравнению со словами.
Во-первых, концепты менее избыточны, чем слова. Они позволяют «сворачивать» синонимы, так что, например, Российская Федерация и Россия понимаются как один термин.
Во-вторых, концепты обладают большей дискриминационной силой, чем слова. Они позволяют определять смысл многозначных слов по их окружению, так что, например, Apple в сочетании с Mac понимается как бренд, а не как фрукт.
 В-третьих, концепты более эффективны, чем слова, при оценке близости текстов. Они позволяют выявить близость между двумя текстами, даже если те не содержат ни одного общего слова, как, например, тексты «Пеле – выдающийся бомбардир» и «Эдсон Арантис ду Насименту – лучший форвард» (рис. 1).
В-третьих, концепты более эффективны, чем слова, при оценке близости текстов. Они позволяют выявить близость между двумя текстами, даже если те не содержат ни одного общего слова, как, например, тексты «Пеле – выдающийся бомбардир» и «Эдсон Арантис ду Насименту – лучший форвард» (рис. 1).
В приведенном примере под концептами понимаются синонимические ряды, объединяющие слова с одинаковыми или близкими значениями, что характерно для ранних работ в этой области [11, 12]. В более поздних работах под концептами понимаются уже не только ряды синонимов, но и другие категории связанных слов, например, семантические или тематические кластеры [6, 8, 9, 13, 14].
Важнейшей задачей, которая возникает при использовании модели Bag-of-concepts, является выбор концептов, соответствующих (близких) данному тексту [15]. Обычно концепты и тексты индексируются с помощью слов, то есть каждому концепту сопоставляется вектор  =(c1, c2, ..., cn), где n – объем используемого словаря; ci
=(c1, c2, ..., cn), где n – объем используемого словаря; ci  – веса слов в концепте, определяющие их важность для данного концепта. Аналогично каждому тексту сопоставляется вектор
– веса слов в концепте, определяющие их важность для данного концепта. Аналогично каждому тексту сопоставляется вектор  =(w1, w2, ..., wn), где wi
=(w1, w2, ..., wn), где wi  – это веса тех же слов в этом тексте. Близость между концептом и текстом оценивается при помощи какого-либо критерия, оперирующего значениями этих векторов. В результате определяется набор из k
– это веса тех же слов в этом тексте. Близость между концептом и текстом оценивается при помощи какого-либо критерия, оперирующего значениями этих векторов. В результате определяется набор из k  самых близких тексту концептов, который и образует представление текста в новом пространстве. В работе [15] предлагаются две формулы для оценки близости между концептами и текстами. Первая формула предназначена для оценки контекстной близости на основе косинусной меры:
самых близких тексту концептов, который и образует представление текста в новом пространстве. В работе [15] предлагаются две формулы для оценки близости между концептами и текстами. Первая формула предназначена для оценки контекстной близости на основе косинусной меры:
 . (1)
. (1)
Вторая формула предназначена для оценки ранговой близости на основе коэффициента корреляции Спирмена, определяющего, насколько совпадает порядок слов в концепте и в тексте:
 (2)
(2)
где T – это количество слов, входящих одновременно и в текст, и в концепт; rank – функция, возвращающая ранг (позицию) заданного слова в заданном тексте или в концепте.
Покажем, для чего нужна ранговая близость, на примере концепта «Женский футбол». Для указанного концепта высший приоритет имеют слова «женский» и «футбол». Если сравнивать два текста «Женский футбол – это захватывающее зрелище» и «Когда мужчины смотрят футбол, женские чары теряют силу», то очевидно, что, хотя оба текста содержат слова «женский» и «футбол», они имеют разное отношение к рассматриваемому концепту. Первый текст полностью коррелирует с этим концептом, а второй вообще не связан с ним. Здесь, помимо контекстной близости, важен относительный порядок слов в тексте. Поэтому в статье [15] предлагается использовать комбинированную оценку близости на основе контекстной и ранговой близости:
 . (3)
. (3)
Подходы на основе модели контекстных векторов. Еще одним расширением модели Bag-of-words, позволяющим учитывать связи между словами, является модель контекстных векторов [4, 16–19]. Как следует из названия, модель формирует так называемые контекстные векторы слов, показывающие зависимость каждого слова от всех других слов используемого пространства. В этом состоит принципиальное отличие модели контекстных векторов от модели концептов, которая учитывает не все, а только избранные зависимости (связи) между словами.
Выделяют два основных способа вычисления контекстных связей между словами: низкоуровневый (на основе дистрибутивного анализа) и высокоуровневый (на основе специальных таксономий) [4]. При низкоуровневом способе для оценки контекстных связей используются частоты или вероятности совместного появления слов [18, 19]. При высокоуровневом способе для оценки контекстных связей используются расстояния между семантическими классами, соответствующими словам в онтологии или в тезаурусе [20]. Например, очень часто для таких целей используется тезаурус WordNet [16, 21].
Контекстные векторы n-мерного пространства, записанные вместе, образуют квадратную матрицу «термины-на-термины» размерности n´n (табл. 1). Эту матрицу также часто называют матрицей попарных связей или матрицей зависимостей, поскольку каждый ее элемент (i, j)  – не что иное, как численное выражение семантической связи между i-м и j-м словами (терминами).
– не что иное, как численное выражение семантической связи между i-м и j-м словами (терминами).
Таблица 1
Матрица семантических связей, образованная контекстными векторами
Table 1
A semantic link matrix created from context vectors
| |
С1
|
С2
|
…
|
Cn
|
|
Термин 1
|
Термин 2
|
…
|
Термин n
|
|
Термин 1
|
c11
|
c12
|
…
|
c1n
|
|
Термин 2
|
c21
|
c22
|
…
|
c2n
|
|
….
|
…
|
…
|
…
|
…
|
|
Термин n
|
cn1
|
cn2
|
…
|
cnn
|
Матрица семантических связей играет ключевую роль в формировании семантически обогащенных представлений текстов в пространстве контекстных векторов [16, 19]. По сути она является оператором перехода из одного пространства дескрипторов в другое.
Действительно, пусть текст d в исходном n-мерном пространстве несвязанных терминов имеет представление  =(w1, w2, ..., wn), где w1, w2, ..., wn – это веса терминов в рассматриваемом тексте. Матрица семантических связей (назовем ее R) позволяет отобразить это исходное представление текста
=(w1, w2, ..., wn), где w1, w2, ..., wn – это веса терминов в рассматриваемом тексте. Матрица семантических связей (назовем ее R) позволяет отобразить это исходное представление текста  в новое представление
в новое представление  , отражающее связи между словами и в то же время сохраняющее информацию исходного представления:
, отражающее связи между словами и в то же время сохраняющее информацию исходного представления:
 (4)
(4)
Формула (4) дает сжатую форму записи представления текста в пространстве контекстных векторов. Развернув формулу, получим, что такое представление текста – не что иное, как линейная комбинация контекстных векторов:
 (5)
(5)
 Подходы на основе латентной семантической модели. Еще один класс подходов, преодолевающих ограничение модели Bag-of-words, направлен на создание представлений текстов c помощью латентных тематик. Формирование таких представлений осуществляется путем факториза- ции матрицы «документы-на-термины» [22, 23]. Наиболее популярным методом среди подходов данного класса является латентный семантический анализ (LSA), который в качестве факторизации использует сингулярное разложение [24]. Сингулярное разложение позволяет заменить исходную матрицу размерности m´n ортогональными матрицами размерностей m´k и k´n соответственно и диагональной матрицей размерности k´k (рис. 2). При такой замене большая часть малозначимой и случайной информации теряется, зато отчетливей проявляются скрытые тематические тренды. По сути эти скрытые тренды представляют те же самые тематические концепты, только извлеченные особым способом.
Подходы на основе латентной семантической модели. Еще один класс подходов, преодолевающих ограничение модели Bag-of-words, направлен на создание представлений текстов c помощью латентных тематик. Формирование таких представлений осуществляется путем факториза- ции матрицы «документы-на-термины» [22, 23]. Наиболее популярным методом среди подходов данного класса является латентный семантический анализ (LSA), который в качестве факторизации использует сингулярное разложение [24]. Сингулярное разложение позволяет заменить исходную матрицу размерности m´n ортогональными матрицами размерностей m´k и k´n соответственно и диагональной матрицей размерности k´k (рис. 2). При такой замене большая часть малозначимой и случайной информации теряется, зато отчетливей проявляются скрытые тематические тренды. По сути эти скрытые тренды представляют те же самые тематические концепты, только извлеченные особым способом.
Тот же принцип извлечения скрытых тематик лежит в основе метода неотрицательной матричной факторизации (NMF) [25, 26], но вместо сингулярного разложения он использует разложение матрицы в произведение двух неотрицательных матриц (рис. 3). В работе [27] оба указанных метода (LSA и NMF) сравниваются по их способности к улучшению качества классификации текстов и делается вывод о превосходстве метода LSA.

Предлагаемый подход к автоматической классификации текстов
Основная идея предлагаемого подхода. В данной работе предлагается обогащать представления текстов семантическими связями, которые извлека- ются из этих же текстов. Под извлечением семан- тических связей, как обычно, понимается задача распознавания отношений, имеющих место между двумя и более сущностями в тексте [28]. Для извлечения семантических связей используется статистика совместной встречаемости слов. Идея, лежащая в основе этого подхода, лаконично выражена в следующей знаменитой фразе: «You shall know a word by the company it keeps» [29]. Авторы опираются на эту идею, полагая, что чем чаще два слова встречаются «в одной компании» (в данном случае в текстах одной тематики), тем сильнее между ними семантическая связь.
Статистику совместной встречаемости слов предоставляет матрица «документы-на-термины», описывающая распределение слов (терминов) в текстах (документах обучающей коллекции). Как следует из названия матрицы, ее строками являются документы, столбцами – термины, а элементами – частоты употребления терминов в документах (рис. 4). Поскольку «такие частотные матрицы имеют склонность быть разреженными и зашумленными, особенно если обучающая коллекция относительно мала в размерах» [30], авторы считают целесообразным до использования этой матрицы применить к ней два основных преобразования: редукцию и сингулярное разложение.

Редукция матрицы «документы-на-термины». Первое преобразование матрицы «документы-на-термины» заключается в редукции размерности этой матрицы, то есть в отбрасывании части ее столбцов и строк. Редукция необходима для извлечения семантических связей, которые относятся к интересующей нас теме (предметной области). Первым делом отсекаем «лишние» столбцы матрицы, соответствующие терминам других тем. Для этой цели можно использовать различные дискриминационные критерии [31, 32]. В данном случае используется критерий Пирсона (Хи-квадрат), который оценивает распределение каждого термина в текстах рассматриваемой темы (позитивном множестве) и текстах других тем (негативном множестве):
 (6)
(6)
где A, B – количество документов позитивного множества, содержащих и не содержащих данный термин соответственно; C, D – количество документов негативного множества, содержащих и не содержащих данный термин соответственно [31]. Значение данного критерия тем выше, чем чаще термин встречается в документах позитивного множества и чем реже в документах негативного множества. Этот факт позволяет нам отобрать термины с самыми высокими значениями критерия, то есть ключевые слова рассматриваемой темы.
 Затем отсекаем «лишние» строки матрицы, соответствующие документам негативного множества. В результате получаем редуцированную матрицу «документы-на-термины», строки которой соответствуют текстам рассматриваемой темы, а столбцы – ее ключевым словам (рис. 5).
Затем отсекаем «лишние» строки матрицы, соответствующие документам негативного множества. В результате получаем редуцированную матрицу «документы-на-термины», строки которой соответствуют текстам рассматриваемой темы, а столбцы – ее ключевым словам (рис. 5).
Сингулярное разложение матрицы «документы-на-термины». Второе преобразование матрицы «документы-на-термины» состоит в ее сингулярном разложении. Сингулярное разложение – это способ представления произвольной чис- ловой матрицы A размерности m´n (m>n) в виде произведения трех матриц:
A=USVT, (7)
где U и V – ортогональные матрицы размерностей m´n и n´n соответственно (столбцы этих матриц называют левыми и правыми сингулярными векторами); S – диагональная матрица размерности m´n (ее диагональные элементы называют сингулярными числами) (рис. 6).

Согласно теореме Эккарта–Янга, сингулярное разложение позволяет снизить шум и разреженность исходной матрицы, заменяя ее матрицей той же размерности, но меньшего ранга, в которой сохранена только самая значимая информация [33]. Более формально эта теорема звучит следующим образом.
Теорема 1 (Эккарт–Янг). Пусть дана матрица A размерности m´n, для которой известно сингулярное разложение A=USVT и которую требуется аппроксимировать матрицей Ak с заданным рангом k
Ak=USkVT (8)
даст наилучшее приближение исходной матрицы A ранга k в смысле нормы Фробениуса. Если при этом элементы матрицы S отсортированы по убыванию s1³s2³sN³0, то выражение (5) может быть записано в другой форме:
Ak=UkSkVkT, (9)
где Uk и Vk – это матрицы, полученные выделением первых  столбцов из матриц U и V соответственно (рис. 7). Сингулярное разложение, представленное равенством (6), называется экономным, поскольку в случае, когда k намного меньше m и n, оно позволяет произвести существенное сжатие исходной информации.
столбцов из матриц U и V соответственно (рис. 7). Сингулярное разложение, представленное равенством (6), называется экономным, поскольку в случае, когда k намного меньше m и n, оно позволяет произвести существенное сжатие исходной информации.

Сжатие понимается в том смысле, что часть информации, передаваемой исходной матрицей, теряется, а сохраняется только самая важная (доминантная) информация. Потеря информации происходит за счет пренебрежения малыми сингулярными числами, поэтому, чем больше сингулярных чисел отброшено, то есть чем меньше k, тем значительнее эта потеря.
Построение матрицы семантических связей «термины-на-термины» и ее использование для обогащения представлений текстов. Редуцированную и очищенную от шума матрицу «документы-на-термины» будем использовать для построения матрицы семантических связей «тер- мины-на-термины». Поскольку в матрице «документы-на-термины» каждый термин представляет собой вектор-столбец, семантическую связь между любыми двумя терминами можно трактовать как близость или расстояние между соответствующими этим терминам векторами, используя любые известные меры близости или расстояния [34]. В данной работе используем косинусную меру:
 (10)
(10)
где  – вектор-столбцы матрицы «документы-на-термины», соответствующие i-му и j-му терминам соответственно (i, j пробегают весь список терминов); rij
– вектор-столбцы матрицы «документы-на-термины», соответствующие i-му и j-му терминам соответственно (i, j пробегают весь список терминов); rij – значение близости, элемент матрицы семантических связей (рис. 8).
– значение близости, элемент матрицы семантических связей (рис. 8).
Определение косинуса в первом квадранте декартовых координат позволяет утверждать, что максимально возможное значение близости между терминами равно 1, а минимально возможное – 0. Поскольку нас интересуют только самые сильные и устойчивые связи, не будем принимать во внимание значения близости ниже некоторого порога. Иными словами, будем отсекать слабые связи, обнуляя элементы матрицы, значения которых меньше порогового значения.
Использование матрицы семантических связей «термины-на-термины» для формирования новых представлений текстов. Построенная матрица семантических связей R=(rij) используется для отображения представлений текстов в пространство связанных слов. В работе [16] для выполнения такого отображения используется формула (4). Если говорить в целом, то применение этой формулы увеличивает в представлениях текстов веса тех слов, которые имеют сильные семантические связи с другими словами. Увеличение весов происходит даже для тех слов, которые первоначально имели нулевые веса, то есть отсутствовали в исходных представлениях текстов. На следующем примере покажем, что в некоторых случаях это может негативно повлиять на качество работы классификатора.
Пример. Пусть коллекция из трех текстов индексируется ключевыми словами sea, cargo и cruise:
Text1={2sea, 1cargo, 0cruise} ={2, 1, 0},
Text2={1sea, 0cargo, 2cruise} ={1, 0, 2},
Text3={2sea, 0cargo, 1cruise} ={2, 0, 1}.
Известно, что текст 1 относится к теме «Морские грузоперевозки», а текст 2 не относится к этой теме. Про текст 3 ничего не известно, однако отсутствие в этом тексте слова cargo и присутствие слова cruise позволяют предположить, что он, как и текст 2, относится, скорее, к теме «Морские путешествия», чем к теме «Морские грузоперевозки». Математическая оценка близости между текстами (на основе косинусной меры) не вносит ясности, так как оказывается, что текст 3 одинаково близок и к тексту 1, и к тексту 2:
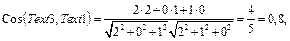

Матрица семантических связей для темы «Морские грузоперевозки» имеет вид
 .
.
Подстановка этой матрицы в формулу (4) позволяет получить новые представления текстов, обогащенные семантическими связями:
Text1={3sea, 3cargo, 0cruise} ={3, 3, 0},
Text2={1sea, 1cargo, 2cruise} ={1, 1, 2},
Text3={2sea, 2cargo, 1cruise} ={2, 2, 1}.
Очевидно, в представлении текста 3 появилось ранее отсутствовавшее там слово cargo. Причем вес слова cargo благодаря сильной связи со словом sea увеличился с 0 до 2. Как результат, близость между текстом 3 и текстом 1 тоже увеличилась и даже стала больше, чем близость между текстом 3 и текстом 1:


Таким образом, в результате использования формулы (4) мы получили в представлении текста 3 ненужное там слово cargo, обеспечившее ложное «смещение» текста 3 к теме «Морские грузоперевозки». Приведенный пример демонстрирует несостоятельность формулы (4) в случае бинарной классификации, когда тексты из разных тем имеют общие ключевые слова. В приведенном примере таким общим для двух тем словом являлось слово sea, которое привело к включению в новое представление текста слова cargo, невзирая на его нулевой вес в исходном представлении текста. В данной работе авторы предлагают модифицировать формулу (4) с учетом наличия нулевых весов в исходных представлениях текстов.
Пусть дано исходное представление текста в виде вектора Text=(w1, ..., wn), где wi  – веса слов в этом тексте; n
– веса слов в этом тексте; n  – размерность пространства слов. Пусть задана матрица семантических связей R=(rij), где
– размерность пространства слов. Пусть задана матрица семантических связей R=(rij), где  . Тогда веса слов
. Тогда веса слов  в новом представлении текста Text¢=(w¢1, ..., w¢n) будем определять по правилу:
в новом представлении текста Text¢=(w¢1, ..., w¢n) будем определять по правилу:

 (11)
(11)
Эксперименты
Исходные данные для классификации. Для проведения экспериментов по бинарной класси- фикации текстов была использована стандартная коллекция Reuters-21578, состоящая из 21 578 документов, распределенных между 135 пересекающимися темами. Как и в работах [1, 35], для классификации были использованы только 12 самых крупных тем коллекции. Для каждой выбранной темы сформировано по 100 корпусов, содержащих все документы этой темы (позитивное множество) и примерно столько же выбранных случайным образом документов из других тем (негативное множество). При формировании корпусов соблюдались предустановленная разбивка документов на обучающие и тестовые, а также баланс между их количеством. В таблице 2 приведены примеры корпусов для каждой из 12 выбранных тем.
Таблица 2
Примеры корпусов для одного эксперимента для каждой из 12 тем
Table 2
Samples корпусов for one experiment for each of 12 subjects
|
№
|
Тема классификации
|
Количество документов в корпусе
|
Количество слов в корпусе
|
|
Всего
|
Из них относящихся к данной теме (позитивное множество)
|
Всего
|
Из них ключевых слов
|
Из них ключевых слов, относящихся к данной теме
|
|
1
|
acq
|
4073
|
2117
|
20464
|
2595
|
1084
|
|
2
|
corn
|
408
|
208
|
5836
|
394
|
271
|
|
3
|
crude
|
1001
|
507
|
10853
|
929
|
747
|
|
4
|
earn
|
6874
|
3751
|
22500
|
4978
|
182
|
|
5
|
grain
|
1017
|
507
|
9514
|
791
|
512
|
|
6
|
interest
|
772
|
388
|
8405
|
717
|
428
|
|
7
|
money-fx
|
1174
|
595
|
10696
|
1144
|
780
|
|
8
|
oilseed
|
316
|
161
|
5271
|
286
|
210
|
|
9
|
ship
|
551
|
277
|
7647
|
581
|
405
|
|
10
|
sugar
|
304
|
153
|
5435
|
317
|
237
|
|
11
|
trade
|
874
|
441
|
9641
|
1159
|
962
|
|
12
|
wheat
|
513
|
264
|
6474
|
437
|
270
|
Метод и способ оценки результатов классификации. Классификация проводилась с помощью свободно распространяемого пакета вычислений R. В качестве алгоритма классификации использовалась машина опорных векторов (Support Vector Machine – SVM). В качестве итоговой оценки результатов классификации по каждой из 12 выбранных тем использовалось среднее значение F-меры в серии из 100 экспериментов. F-мера – это очень популярная мера оценки качества классификации, представляющая собой среднее гармоническое между точностью (P) и полнотой (R) классификации:
 Каждый участвующий в эксперименте корпус текстов сначала подвергался токенизации (делению на слова), затем очищался от стоп-слов. Стемминг и лемматизация не проводились. При формировании представлений документов использовались не все слова, а только ключевые, то есть те, для которых значение критерия Хи-квадрат превысило критическое значение 6,6 (рис. 9). Это критическое значение было определено по специальной таблице, исходя из числа степеней свободы (для данной задачи равное 1) и уровня значимости, равного 1 % [36]. (Следует отметить, что попутно были проверены другие критические значения в диапазоне от 1 до 10, то есть авторы увеличивали или сокращали список ключевых слов, регулируя его длину с помощью фильтра по критическому значению. Серия промежуточных экспериментов показала, что для задачи бинарной классификации список ключевых слов, определяемый значением 6,6, является оптимальным, то есть применение этого значения стабильно обеспечивает лучший результат классификации по сравнению с другими критическими значениями как при использовании традиционной модели Bag-of-words, так и при использовании рассматриваемой модели.)
Каждый участвующий в эксперименте корпус текстов сначала подвергался токенизации (делению на слова), затем очищался от стоп-слов. Стемминг и лемматизация не проводились. При формировании представлений документов использовались не все слова, а только ключевые, то есть те, для которых значение критерия Хи-квадрат превысило критическое значение 6,6 (рис. 9). Это критическое значение было определено по специальной таблице, исходя из числа степеней свободы (для данной задачи равное 1) и уровня значимости, равного 1 % [36]. (Следует отметить, что попутно были проверены другие критические значения в диапазоне от 1 до 10, то есть авторы увеличивали или сокращали список ключевых слов, регулируя его длину с помощью фильтра по критическому значению. Серия промежуточных экспериментов показала, что для задачи бинарной классификации список ключевых слов, определяемый значением 6,6, является оптимальным, то есть применение этого значения стабильно обеспечивает лучший результат классификации по сравнению с другими критическими значениями как при использовании традиционной модели Bag-of-words, так и при использовании рассматриваемой модели.)
Веса ключевых слов в представлениях документов вычислялись с помощью метрики Tf×Idf, которая равна частоте слова в документе Tf, умноженной на обратную документную частоту Idf, то есть на величину, обратную частоте данного слова во всех документах рассматриваемой выборки:
Weigth(term) = Tf×Idf.
Сформировав представления документов в пространстве несвязанных ключевых слов Bag-of-words, авторы выполнили классификацию этих документов и использовали полученные результаты в качестве опорных, ориентируясь на которые, можно было бы судить об изменении качества классификации при обогащении представлений документов с помощью матрицы семантических связей.
 Результаты классификации. Сравнительные результаты классификации представлены в табличном виде (табл. 3) и в графическом (рис. 10).
Результаты классификации. Сравнительные результаты классификации представлены в табличном виде (табл. 3) и в графическом (рис. 10).
Как следует из приведенных результатов, прироста качества классификации удалось добиться в 10 темах из 12. В теме acq (второй по величине в коллекции Reuters) прирост качества нулевой, а в теме oilseed – отрицательный. Однако даже с учетом этих двух негативных результатов средний прирост качества по всем темам является положительным и составляет 1,6 %. Следует отметить также положительные выбросы для тем interest и sugar.
В будущих исследованиях предстоит выяснить причины ухудшения качества классификации в теме oilseed, которое наблюдается на фоне благополучных результатов классификации в остальных темах. Еще большего внимания заслуживает исследование причин положительных выбросов, в которых могут лежать возможные пути дальнейшего совершенствования предлагаемых методов.
Таблица 3
Результаты классификации текстов предлагаемым методом
Table 3
Text classification results using the offered method
|
Тема
|
Среднее значение F-меры, %
|
Прирост качества, %
|
|
Опорный результат (BOW)
|
Предлагаемая модель
|
|
acq
|
96,6
|
96,6
|
0,0
|
|
corn
|
88,8
|
90,2
|
1,4
|
|
crude
|
94,8
|
95,9
|
1,1
|
|
earn
|
97,3
|
98,2
|
0,9
|
|
grain
|
90,2
|
91,2
|
1,0
|
|
interest
|
87,5
|
92,8
|
5,3
|
|
money-fx
|
95,0
|
96,2
|
1,2
|
|
oilseed
|
89,7
|
88,1
|
-1,6
|
|
ship
|
93,7
|
95,2
|
1,5
|
|
sugar
|
79,0
|
84,9
|
5,9
|
|
trade
|
89,9
|
90,8
|
0,9
|
|
wheat
|
91,0
|
92,5
|
1,5
|
В заключение отметим, что в данной работе построена математическая модель автоматической классификации текстов на основе известного подхода Bag-of-words, улучшенного за счет вовлечения в процесс классификации информации о семантических связях между словами, выявляемыми на основе статистики совместной встречаемости слов. Для редуцирования размерности матриц, порождаемых в процессе решения данной задачи, применены редукция и сингулярное разложение. Тестирование предложенного метода, проведенное на подмножестве стандартного корпуса документов Reuters-21578, показало некоторое улучшение качества классификации по комбинированному критерию, объединяющему точность и полноту классификации. Результаты проведенного исследо- вания демонстрируют, что традиционные стати- стические методы анализа текстов могут быть улучшены за счет других статистических методов. Вместе с тем наблюдаемые в ходе экспериментов как положительные, так и отрицательные выбросы полученных значений показателя качества классификации требуют дальнейших исследований.
Литература
1. Joachims T. Learning to classify text using support vector machines: Methods, theory and algorithms. Kluwer Academic Publ., 2002, p. 205.
2. Wallach H.M. Topic modeling: beyond bag-of-words. Proc. 23rd Intern. Conf. on Machine learning. ACM, 2006, pp. 977–984.
3. Yang Y., Pedersen J.O. A comparative study on feature selection in text categorization. ICML, 1997, vol. 97, pp. 412–420.
4. Kalogeratos A., Likas A. Text document clustering using global term context vectors. Knowledge and information systems, 2012, vol. 31, no. 3, pp. 455–474.
5. Sahlgren M., Cöster R. Using bag-of-concepts to improve the performance of support vector machines in text categorization. Proc. 20th Intern. Conf. on Computational Linguistics, Association for Computational Linguistics, 2004, p. 487.
6. Huang A. et al. Clustering documents using a Wikipedia-based concept representation. Advances in Knowledge Discovery and Data Mining, Springer Berlin Heidelberg, 2009, pp. 628–636.
7. Shehata S., Karray F., Kamel M.S. An efficient concept-based mining model for enhancing text clustering. Knowledge and Data Engineering, IEEE Transactions on, 2010, vol. 22, no. 10, pp. 1360–1371.
8. Egozi O., Markovitch S., Gabrilovich E. Concept-based information retrieval using explicit semantic analysis. ACM Transactions on Inform. Systems (TOIS), 2011, vol. 29, no. 2, p. 8.
9. Boubekeur F. and Azzoug W. Concept-based indexing in text information retrieval. Int. J. Comput. Sci. Inf. Technol., vol. 5, 2013, pp. 119–136.
10. Huang L. et al. Learning a concept‐based document similarity measure. Journ. of the American Society for Information Science and Technology, 2012, vol. 63, no. 8, pp. 1593–1608.
11. Gonzalo J., Verdejo F., Chugur I. and Cigarrán J. Indexing with WordNet synsets can improve Text Retrieval. Proc. COLING/ACL Workshop Usage of WordNet for Natural Language Processing, 1998, pp. 38–44.
12. Gómez J.M. et al. Concept indexing for automated text categorization. Natural Language Processing and Information Systems, Springer Berlin Heidelberg, 2004, pp. 195–206.
13. Wang P., Domeniconi C. Building semantic kernels for text classification using Wikipedia. Proc. 14th ACM SIGKDD Intern. Conf. on Knowledge discovery and data mining, ACM, 2008, pp. 713–721.
14. Turdakov D.Y. Word sense disambiguation methods. Programming and Comp. Soft., 2010, vol. 36, no. 6, pp. 309–326.
15. Dinh D., Tamine L. Combining global and local semantic contexts for improving biomedical information retrieval. Advances in Information Retrieval. Springer Berlin Heidelberg, 2011, pp. 375–386.
16. Billhardt H., Borrajo D., Maojo V. A context vector model for information retrieval. Journ. of the American Society for Inform. Sc. and Technology, 2002, vol. 53, no. 3, pp. 236–249.
17. Chen K.J., You J.M. A study on word similarity using context vector models. Computational Linguistics and Chinese Language Processing, 2002, vol. 7, no. 2, pp. 37–58.
18. Carrillo M., López-López A. Concept Based Representations as complement of Bag of Words in Information Retrieval. Artificial Intelligence Applications and Innovations, Springer Berlin Heidelberg, 2010, pp. 154–161.
19. Cheng X. et al. Coupled term-term relation analysis for document clustering. Neural Networks (IJCNN), The 2013 Intern. Joint Conf. on. IEEE, 2013, pp. 1–8.
20. Agirre E. et al. A study on similarity and relatedness using distributional and WordNet-based approaches. Proc. of Human Language Technologies: The 2009 Annual Conf. of the North American Chapter of the Association for Computational Linguistics, ACL, 2009, pp. 19–27.
21. Patwardhan S., Pedersen T. Using WordNet-based context vectors to estimate the semantic relatedness of concepts. Proc. EACL 2006 Workshop Making Sense of Sense-Bringing Computational Linguistics and Psycholinguistics Together, 2006, vol. 1501, pp. 1–8.
22. Mashechkin I., Petrovsky M., Popov D., Tsarev D. Automatic text summarization using latent semantic analysis. Programming and Comp. Soft., 2011, vol. 37, no. 6, pp. 299–305.
23. Машечкин И.В., Петровский М.И., Царев Д.В. Методы вычисления релевантности фрагментов текста на основе тематических моделей в задаче автоматического аннотирования // Вычислительные методы и программирование: Новые вычислительные технологии. 2013. Т. 14. № 1. С. 91–102.
24. Deerwester S.C., Dumais S.T., Landauer T.K., Furnas G.W., Harshman R.A. Indexing by latent semantic analysis. JAsIs, 1990, no. 41 (6), pp. 391–407.
25. Xu W., Liu X., Gong Y. Document clustering based on non-negative matrix factorization. In: Proc 26th Annual Intern. ACM SIGIR Conf. on Research and Development in Information Retrieval, 2003, pp. 267–273.
26. Tsarev D., Petrovskiy M., Mashechkin I. Using NMF-based text summarization to improve supervised and unsupervised classification. IEEE 2011 11th Int. Conf. on Hybrid Intelligent Systems (HIS), 2011, pp. 185–189.
27. Stevens K. et al. Exploring topic coherence over many mod- els and many topics. Proc. 2012 Joint Conf. on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, ACL, 2012, pp. 952–961.
28. Banko M., Etzioni O., Center T. The tradeoffs between open and traditional relation ex-traction. In ACL, 2008, vol. 8, pp. 28–36.
29. Firth J.R. A synopsis of linguistic theory 1930–1955. In Studies in linguistic analysis (Spec. vol. of the Philological society), Oxford, Blackwell, 1957, pp. 1–32.
30. Slonim N., Tishby N. The power of word clusters for text classification. In 23rd European Colloquium on Inform. Retrieval Research, 2001, vol. 1.
31. Yang Y., Pedersen J.O. A comparative study on feature selection in text categorization. ICML, 1997, vol. 97, pp. 412–420.
32. Fedorenko D., Astrakhantsev N., Turdakov D. Automatic recognition of domain-specific terms: an experimental evaluation. SYRCoDIS, 2013, pp. 15–23.
33. Eckart C., Young G. The approximation of one matrix by another of lower rank. Psychometrika, 1936, no. 1 (3), pp. 211–218.
34. Chen S., Ma B., Zhang K. On the similarity metric and the distance metric. Theoretical Comp. Sc., 2009, vol. 410, no. 24, pp. 2365–2376.
35. McCallum A., Nigam K. A comparison of event models for naive Bayes text classification AAAI-98 workshop on learning for text categorization. 1998, vol. 752, pp. 41–48.
36. Lancaster H.O. Chi‐Square Distribution. John Wiley & Sons, Inc. 1969, 356 p.

 =(c1, c2, ..., cn), где n – объем используемого словаря; ci
=(c1, c2, ..., cn), где n – объем используемого словаря; ci  – веса слов в концепте, определяющие их важность для данного концепта. Аналогично каждому тексту сопоставляется вектор
– веса слов в концепте, определяющие их важность для данного концепта. Аналогично каждому тексту сопоставляется вектор  =(w1, w2, ..., wn), где wi
=(w1, w2, ..., wn), где wi  самых близких тексту концептов, который и образует представление текста в новом пространстве. В работе [15] предлагаются две формулы для оценки близости между концептами и текстами. Первая формула предназначена для оценки контекстной близости на основе косинусной меры:
самых близких тексту концептов, который и образует представление текста в новом пространстве. В работе [15] предлагаются две формулы для оценки близости между концептами и текстами. Первая формула предназначена для оценки контекстной близости на основе косинусной меры: . (1)
. (1) (2)
(2) . (3)
. (3) – не что иное, как численное выражение семантической связи между i-м и j-м словами (терминами).
– не что иное, как численное выражение семантической связи между i-м и j-м словами (терминами). =(w1, w2, ..., wn), где w1, w2, ..., wn – это веса терминов в рассматриваемом тексте. Матрица семантических связей (назовем ее R) позволяет отобразить это исходное представление текста
=(w1, w2, ..., wn), где w1, w2, ..., wn – это веса терминов в рассматриваемом тексте. Матрица семантических связей (назовем ее R) позволяет отобразить это исходное представление текста  , отражающее связи между словами и в то же время сохраняющее информацию исходного представления:
, отражающее связи между словами и в то же время сохраняющее информацию исходного представления: (4)
(4) (5)
(5)


 (6)
(6)

 столбцов из матриц U и V соответственно (рис. 7). Сингулярное разложение, представленное равенством (6), называется экономным, поскольку в случае, когда k намного меньше m и n, оно позволяет произвести существенное сжатие исходной информации.
столбцов из матриц U и V соответственно (рис. 7). Сингулярное разложение, представленное равенством (6), называется экономным, поскольку в случае, когда k намного меньше m и n, оно позволяет произвести существенное сжатие исходной информации.
 (10)
(10) – вектор-столбцы матрицы «документы-на-термины», соответствующие i-му и j-му терминам соответственно (i, j пробегают весь список терминов); rij
– вектор-столбцы матрицы «документы-на-термины», соответствующие i-му и j-му терминам соответственно (i, j пробегают весь список терминов); rij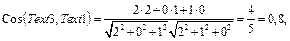

 .
.

 . Тогда веса слов
. Тогда веса слов  в новом представлении текста Text¢=(w¢1, ..., w¢n) будем определять по правилу:
в новом представлении текста Text¢=(w¢1, ..., w¢n) будем определять по правилу:



