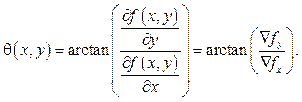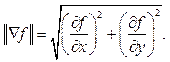Software & Systems

При решении задачи поиска дефектов в поверхностных слоях стальных деталей достаточно часто применяют методы, базирующиеся на анализе рассеяния магнитных полей возле дефектов после намагничивания этих изделий [1]. В локальной области, где нарушена сплошность, происходит изменение магнитного потока. Картина распределения магнитного поля будет определяться глубиной залегания дефекта, его величиной и формой. Например, у поверхностных трещин, ориентированных перпендикулярно магнитному потоку, наблюдается резко выраженное рассеяние магнитного поля. А у дефектов, ориентированных вдоль магнитного потока, поля рассеяния практически не наблюдаются [2].

Одним из наиболее известных методов магнитной дефектоскопии является метод магнитного порошка (ISO 9934-1:2001): на поверхность намагниченной детали высыпают магнитный порошок (сухой метод) или наносят магнитную суспензию (мокрый метод) [3]; магнитные частицы порошка или суспензии, попавшие в зоны магнитных полей рассеяния, осядут на поверхности детали в области нахождения дефектов.

При использовании магнитной дефектоскопии основным намагничиванием является циркулярное. Продольное намагничивание применяют обычно тогда, когда предполагается, что в исследуемом изделии дефекты строго поперечные, или ис- пользование циркулярного намагничивания неприемлемо [4].

При использовании люминесцентных порошков или суспензий на изображениях исследуемых деталей дефекты видны значительно лучше [2], поэтому появляется возможность автоматизированной обработки таких изображений [5, 6]. В данной работе представлена автоматизированная процедура выбора методов обработки изображений с целью обнаружения дефектов.

Выбор метода улучшения изображения

Решение задачи автоматизированного выбора методов обработки изображений начинается с ввода цифровой фотографии исследуемой детали [7, 8]. В настоящее время обычно используют цветное фото [9].

Изображение принято определять через функцию f(x, y), где x и y являются пространственными (плоскостными) координатами, а амплитуду f для каждой пары координат x и y называют интенсивностью или яркостью изображения в точке с этими координатами. Словосочетание уровень серого часто используют для обозначения яркости монохромного изображения. Цветные изображения формируются комбинацией нескольких монохромных изображений. Например, в цветовой системе RGB цветное изображение строится из трех от- дельных монохромных компонент (красной, зеленой и синей). По этой причине многие методы и приемы, разработанные для монохромных изображений, могут быть распространены на цветные изображения путем последовательной обработки трех монохромных компонент.

В качестве примера изображения в данной работе будет обрабатываться фотография приваренного к трубе фланца (рис. 1). Изделие было обработано люминесцентной суспензией Magnaglo 14HF, создавшей люминесцентный зеленый индикаторный рисунок, который наблюдается в ультрафиолетовом свете при длине волны 365 нм.

После загрузки изображения необходимо принять решение об улучшении его качества [9]. Это связано с тем, что надежная идентификация дефектов напрямую зависит от качества анализируемого изображения [10]. Низкое качество может привести к неправильной идентификации или к недостоверному определению характеристик дефектов [11]. В связи с этим надежное качество улучшения по- добных изображений является важной задачей, которую необходимо решать в условиях слабой контрастности и низкой резкости изображений [12].

Общей теории улучшения изображений не существует. Если изображение обрабатывается с целью визуальной интерпретации, то оценку работы конкретного метода дает в конечном счете оператор-исследователь. Методы улучшения настолько разнообразны и используют так много различных подходов к обработке изображения, что трудно собрать осмысленную совокупность подходящих для улучшения методов в одной статье, не проводя отдельное обширное исследование [13–16].

Достаточно часто для улучшения изображений используют фильтрацию. При этом под этим термином наравне с удалением или компенсацией шумов и помех понимается и прямое получение из изображения информации о характеристиках локально неоднородных объектов [17].

Необходимо учитывать, что применение методов цифровой обработки изображений (ЦОИ) для задачи улучшения изображений достаточно часто дает искажение информации об объектах, присутствующих на изображении. Например, следствием повышения контраста и усиления краев достаточно часто является искажение формы и размера дефектоскопического объекта, что крайне нежелательно.

Один из возможных вариантов решения этой проблемы состоит в применении не методов ЦОИ для улучшения изображений, а методов фильтрации полезного сигнала. Но в этом случае под полезным сигналом следует понимать изображения дефектов. Информация от дефектов может быть интерпретирована как локальные неоднородности двумерного конечного нестационарного стохастического сигнала. В этом случае можно решать задачу фильтрации локальных неоднородностей изображений на фоне помех [18].

На рисунке 2 представлена схема автоматизированного выбора алгоритма улучшения изображения.

Как видно из рисунка, в данной методике реализованы следующие методы: инверсная фильтрация, винеровская фильтрация, сглаживающая фильтрация методом наименьших квадратов со связью, алгоритм Люси–Ричардсона итерационного нелинейного восстановления, слепая деконволюция.

Можно отметить, что в последнее время методы слепой деконволюции приобретают все большую популярность.

Для рассматриваемого примера наиболее предпочтительной, на взгляд авторов, оказалась обработка изображения методом Люси–Ричардсона (рис. 3) [19].

Выделение границ объектов на изображении

Задача выделения границ объектов при ЦОИ возникает достаточно часто, например, выделение границ у дефектов. Дело в том, что многие методы распознавания изображений базируются на определении краев. Это связано с тем, что анализ на краях малочувствителен к общей освещенности. Обнаружение краев выделяет контраст (градиент). По определению, контраст – разная яркость. А ввиду того, что контраст между объектами и задним фоном происходит на границах, это обстоятельство и лежит в основе выделения границы объектов на изображении. Можно отметить, что и человеческое зрение выделяет границы объектов таким же образом.

Существует достаточно много математических методов выделения границ, но все они базируются на операции дифференцирования (в непрерывном случае) или замене конечными разностями в дискретном случае. Кроме того, практически все методы можно разделить на два семейства, которые базируются на поиске максимумов или нулей.

Те методы, которые базируются на поиске максимумов, определяют границы при помощи вычис- ления силы края, например, вычисление значений первой производной. После этого производится поиск локальных максимумов силы края с использованием информации о предполагаемом направлении границы, которое достаточно часто перпендикулярно вектору градиента.

Так как интенсивность изображения задается функцией от двух переменных f(x, y), ее градиент показывает направление максимального изменения интенсивности и вычисляется следующим образом: .

Направление градиента (угол) вычисляют по формуле

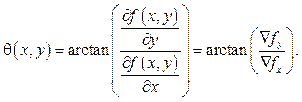
Сила края задается длиной градиента:

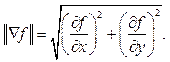
С помощью методов поиска нулей вычисляются пересечение оси абсцисс с выражением для второй производной. Достаточно часто это нули лапласиана или нули нелинейного дифференциального выражения.

Начальным шагом при решении задачи выделения границ достаточно часто служит сглаживание изображения, обычно это фильтр Гаусса.

Методы выделения границ различаются используемыми фильтрами сглаживания и способами расчета силы края. Большинство методов выделения границ базируются на вычислениях градиента изображения, все они различаются по типу применяемых фильтров, которые служат для вычисления градиентов в направлениях x и y.

Обозначенную проблему можно решать при помощи алгоритмов выделения контуров. Наиболее часто применяются методы Собеля, Превитта и Робертса, использующие базовое свойство сигнала яркости – разрывность. Самый общий алгоритм нахождения разрывов состоит в использовании скользящей маски, которую также называют фильтром, окном, ядром или шаблоном. По сути маска – это квадратная матрица, которая поставлена в соответствие заданному множеству пикселей в исходном изображении. Элемент матрицы называют коэффициентом. Математические преобразования для локальных областей изображения с использованием этой матрицы называют пространственной фильтрацией, или просто фильтрацией.

Процесс пространственной фильтрации базируется на линейном перемещении маски фильтра от одного пикселя изображения к другому – в каждом месте (x, y) отклик фильтра рассчитывается с уче- том заранее определенных зависимостей. Для случая линейной пространственной фильтрации отклик задают при помощи суммы произведения коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской фильтра.

В задаче обнаружения перепадов яркости используют дискретные аналоги производных первого и второго порядков.

Морфологическая обработка изображений

После получения изображения удовлетворительного для исследователя качества проводится морфологическая обработка этого изображения. Такая обработка нужна для извлечения определенных компонентов изображения, другими сло- вами, для обнаружения дефектов, то есть для ре- шения поставленной задачи. На рисунке 4 в виде схемы представлен процесс решения задачи, а на рисунке 5 – этап морфологической обработки изображения.

Продемонстрируем работу этого этапа на обработке изображения, приведенного на рисунке 3.

Для начала необходимо провести бинаризацию изображения, то есть значения пикселов изображения приравнять к 1 или 0 (рис. 6). При помощи морфологической реконструкции очистим изображение от объектов, соприкасающихся с границей (рис. 7), и произведем утоньшение границ объектов на изображении. Результат представлен на рисунке 8.

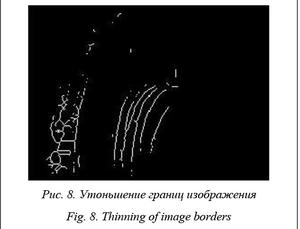
Далее на полученном изображении выделим компоненты связности. На рисунке 8 имеются 56 компонент связности. Это означает, что на изображении присутствуют 56 объектов. При помощи операции морфологического замыкания с использованием компонент связности на изображении удалим небольшие объекты. Результат представлен на рисунке 9.

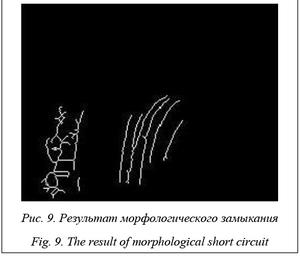
Для полученного изображения определим компоненты связности. Их осталось семь. Используя эти данные, рассчитаем диаметры для оставшихся объектов.

Объект с наименьшим диаметром можно удалить.

Далее, анализируя рисунки 9 и 3, можно сделать вывод о том, что два левых объекта на рисунке 9 не являются результатом сварочных работ (отверстие и грани фланца). Поэтому они не учитываются при выработке решения о наличии дефектов во фланце.

В результате работы алгоритма специалист получает информацию, на основании которой делает вывод о наличии или отсутствии дефектов в исследуемом изделии. В рассмотренном примере видно, что линии (объекты справа) непрерывны и не имеют резкой смены направлений. Поэтому можно сделать вывод об отсутствии нарушений сплошности (дефектов) в изделии.

Следует заметить, что бинарные изображения по желанию исследователя можно инвертировать.

Инструментарий, применяемый при обработке изображений, может быть совершенно различным [20]. Авторы в ходе представленных исследований использовали MATLAB [21].

Необходимо отметить, что данная процедура является открытой, то есть к ней можно (и даже нужно) подключать различные методы для работы с цифровыми изображениями, например, для реконструкции смазанных изображений. В этом случае необходимо использовать интегральное уравнение Фредгольма I рода, решение которого представляет собой достаточно сложную задачу. Поэтому привлечение различных методов, например тихоновской регуляризации, является необходимым условием.

Литература

1.     Неразрушающий контроль; [под общ. ред. В.В. Клюева]. Т. 1. Кн. 1: Соснин Ф.Р. Визуальный и измерительный контроль. М.: Машиностроение, 2008. 323 с.

2.     Исаев М.А., Круглов И.А. Дефекты сварных соединений. Фотоальбом: практич. пособие. М.: Спектр, 2013. 84 с.

3.     Шелихов Г.С., Глазков Ю.А. Магнитопорошковый контроль: учеб. пособие. М.: Спектр, 2011. 183 с.

4.     Шелихов Г.С. Магнитопорошковая дефектоскопия М.: Спектр,  2010. 336 с.

5.     Gonzalez R.C., Woods R.E. Digital image processing. Pearson Intern. Edition prepared by Pearson Education, 2008, 954 p.

6.     Конушин А., Баринова О., Конушин В., Якубенко А., Велижев А. Введение в компьютерное зрение. 2013. URL: http://courses.graphicon.ru/files/courses/vision/2010/cv_2010_01.pdf (дата обращения: 13.06.16).

7.     Фисенко В.Т., Фисенко Т.Ю. Компьютерная обработка и распознавание изображений: учеб. пособие. СПб: Изд-во СПбГУ ИТМО, 2008. 192 с.

8.     Gatchin Y.A., Zharinov I.O., Korobeynikov A.G., Zhari- nov O.O. Theoretical estimation of grassmann's transformation resolution in avionics color coding systems. Modern Applied Scien­ce, 2015, vol. 9, no. 5, рр. 197–210.

9.     Гришенцев А.Ю., Коробейников А.Г. Методы и модели цифровой обработки изображений. СПб: Изд-во Политехн. ун-та, 2014. 190 с.

10.   Красильников Н.Н. Реставрация изображений с учетом их структуры // Оптический журнал. 2009. Т. 76. № 2. С. 7–12.

11.   Красильников Н.И. Цифровая обработка 2D- и ЗD-изо­бражений: учеб. пособие. СПб: БХВ-Петербург, 2011. 608 с.

12.   Jahne B. Digital Image Processing. Springer Sc. & Business Media, 2005, 608 p.

13.   Tschumperle D. Fast anisotropic smoothing of multi-valued images using curvature-preserving. PDE’s Init’l Jour. on Comp. Vision, 2006, no. 68 (1), рр. 65–82.

14.   Богатырев В.А., Богатырев А.В. Функциональная на­дежность систем реального времени // Науч.-технич. вестн. ин­форм. технологий, механики и оптики. 2013. № 4. С. 150–151.

15.   Коробейников А.Г., Кудрин П.А., Сидоркина И.Г. Алгоритм распознавания трехмерных изображений с высокой детализацией // Вестн. Поволж. гос. технологич. ун-та. Сер.: Радиотехнич. и инфокоммуникационные системы. 2010. № 2. С. 91–98.

16.   Коробейников А.Г., Алексанин С.А. Методы автоматизированной обработки изображений при решении задачи магнитной дефектоскопии // Кибернетика и программирование. 2015. № 4. С. 49–61; DOI: 10.7256/2306-4196.2015.4.16320; URL: http://e-notabene.ru/kp/article_16320.html (дата обращения: 13.06.16).

17.   Liu C., Szeliski R., Sing Bing Kang, Zitnick C.L., Free- man W.T. Automatic estimation and removal of noise from a single image // LEEI Transactions on Pattern Analysis and Machine Intelligence, 2008, vol. 30.1, no. 2, рр. 299–314.

18.   Voskoboynikov Yu.E. A combined nonlinear contrast image reconstruction algorithm under inexact point-spread function. Optoelectronics, Instrumentation and Data Processing, 2007, no. 6, рр. 489–499.

19.   Кирьянов К.А. Инструментальная реализация алгоритмов реконструкции искаженных изображений // GraphiCon-2010: сб. тр. 20-й Междунар. конф. СПб: Изд-во СПбГУ ИТМО, 2010. С. 188–191.

20.   Визильтер Ю.В, Желтов С.Ю., Князь В.А. и др. Обработка и анализ цифровых изображений с примерами на LabVIEW IMAQ Vision. М.: ДМК Пресс, 2007. 464 с.

21.   Gonzalez R.C., Woods R.E., Eddins S.L. Digital image processing using MATLAB. Gatesmark Publ. a Division of Gatesmark, LLC, 2009, 827 p.