В настоящее время задача реконструкции и развития транспортной системы страны сталкивается с трудностями поиска оптимальных мест размещения транспортных коммуникаций. Современные решения по размещению элементов транспортных систем не всегда отвечают требованиям рациональности вследствие сложности и многовариантности задач. Основной проблемой является то, что строительство транспортных объектов производится однократно, в то время как эксплуатация – в течение многих десятилетий [1].
 Основной идеей для повышения эффективности транспортных сетей является создание многоуровневой инфраструктуры (см. рис. 1) с центрами обслуживания на каждом уровне [2].
Основной идеей для повышения эффективности транспортных сетей является создание многоуровневой инфраструктуры (см. рис. 1) с центрами обслуживания на каждом уровне [2].
В работе решается задача выбора мест расположения транспортных объектов при заданных координатах точек производств, их объемах продукции, а также при заданной сети дорог в виде множества точек (станций), где возможно построение логистических центров. В качестве критерия оптимизации выступают общие затраты на перевозку и создание новых объектов инфраструктуры. Поскольку объемы перевозимой продукции фиксированные, оптимизация связана прежде всего с сокращением расстояний при перевозках от производств до логистических центров и обратно [1].
Постановка задачи оптимального размещения транспортных объектов на основе теории центров обслуживания потребителей приводит к многоразмерным задачам дискретной оптимизации на основе переборных алгоритмов NP-сложности и не позволяет решать поставленные задачи для десятков тысяч предприятий и тысяч железнодорожных станций [2–4].
Классические задачи о кратчайшем расстоянии между точками и их центром на плоскости решаются, когда точки, для которых находится центр, заданы. В общем случае оптимизация расстояний от точек до центров подмножеств точек должна достигаться вариацией самих подмножеств точек, что приводит к задаче оптимальной кластеризации исходного множества точек и определения оптимальных центров кластеров. Известно, что при боль- ших n полный перебор таких вариантов определяется величиной порядка kn–1, где k – количество кластеров, а n – количество точек (производств). Поэтому для практических задач необходимы методы, радикально уменьшающие перебор вариантов [4, 5].
Математическая модель размещения транспортных объектов на основе кластерного анализа
В данной работе для оптимального выбора мест расположения контейнерных пунктов (КП) и контейнерных накопительно-распределительных центров (КНРЦ) предлагается применить универсальную методологию разбиения множества объектов с заданными свойствами на подмножества при заданных критериях разбиения и получения центров этих подмножеств, обладающих оптимальными свойствами. В качестве такой универсальной процедуры предлагается использовать математические методы кластеризации объектов, известные как кластерный анализ [5, 6].
Геометрическая близость объектов от центра гарантирует минимизацию расстояний при перевозке, а учет веса каждого объекта, выражающего объем перерабатываемой объектом продукции, оптимизирует общие затраты на перевозки. Большое достоинство кластерного анализа и в том, что он позволяет производить разбиение объектов не по одному параметру, а по целому набору признаков. Анализ литературы по кластерному анализу и опыт использования стандартных программных средств кластерного анализа позволяют утверждать, что принципиально возможно решать поставленные задачи для практических задач большой размерности (для федеральных округов и всей страны в целом) [7, 8].
Однако при подходе к решению практических задач оптимизации местоположения КП и КНРЦ на основе идеи кластеризации возникла новая проблема, решение которой развивает сами методы кластерного анализа.
Так, при применении алгоритмов кластеризации по известному методу k-means [6] считается, что оптимальный центр может находиться в любой точке пространства параметров, определяющих объекты. Если параметры – это геометрические координаты центров производства, то центр лежит в любой точке плоскости. На практике следует рассмотреть случай, когда центр обязательно должен находиться в одной из заданных точек (например, на железнодорожной линии или станции). Таким образом, при решении задачи определения мест КП и КНРЦ приходится решать задачу кластеризации с проекцией на функцию, когда центр обязательно должен находиться на железнодорожной магистрали, или с проекцией на точки – на железнодорожной станции.
В работе предлагается новый алгоритм класте- ризации с проекцией на множество точек, названный k-means pro, и исследуется возможность его применения в практических задачах проектирования транспортной инфраструктуры [4].
Входными данными алгоритма являются множество объектов кластеризации X = {x1, …, xn}, их веса V = {v1, …, vn} и допустимое множество проекций Y = {y1, …, yp}. Каждый j-й объект и каждая допустимая точка-проекция заданы в G-мерном пространстве RG, то есть xj = (xj1, …, xjG) и yr = (yr1, …, yrG).
Единственным управляющим параметром является число кластеров k, на которые производится разбиение S = {S1, …, Sk} множества Х. В результате получается несмещенное разбиение S* = {S*1, …, S*k}, центры которого – это оптимальное множество проекций C* Í Y.
Введем следующие обозначения: n – количество объектов кластеризации; p – количество точек допустимого множества проекций; i, i’ – номер кластера; j – номер объекта; r – номер точки множества проекций; l – номер координаты точки; m – номер текущей итерации; G – размерность пространства, в котором выполняется кластеризация.
Расстояние между точками в G-мерном пространстве определяется по евклидовой метрике, где tl и t2 – две любые точки пространства RG:

Алгоритм k-means pro.
1. Выберем начальное разбиение
 ,
,

2. Пусть построено m-е разбиение
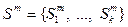 .
.
Вычислим набор векторов средних  , то есть
, то есть  ,
,
где  ; ni – количество точек i-го кластера.
; ni – количество точек i-го кластера.
3. Определим множество проекций средних для текущего разбиения:
 .
.
4. Построим минимальное дистанционное разбиение, порождаемое множеством Cm, и возьмем его в качестве  то есть
то есть
5. Если Sm+1 ¹ Sm, то переходим к п. 2, заменив m на m+1; если Sm+1 = Sm, то полагаем Sm = S*, Cm = C* и заканчиваем работу алгоритма.
Поскольку на последовательности разбиений S0, S1, …, Sm, строящейся в алгоритме, функционал качества разбиений  не возрастает, причем F(Sm) = F(Sm+1), только если Sm=Sm+1, для любого начального разбиения S0 алгоритм через конечное число шагов заканчивает работу. Сложность вычислений по этому алгоритму оценивается как O(nkm), где n – количество кластеризуемых объектов; k – количество кластеров; m – количество итераций.
не возрастает, причем F(Sm) = F(Sm+1), только если Sm=Sm+1, для любого начального разбиения S0 алгоритм через конечное число шагов заканчивает работу. Сложность вычислений по этому алгоритму оценивается как O(nkm), где n – количество кластеризуемых объектов; k – количество кластеров; m – количество итераций.
Начальное разбиение  выбирается произвольным образом, например так: из всего множества координат объектов выбираются минимальное и максимальное число по x и по y, затем в этом диапазоне выбираются k точек (начальных центров кластеров). В данной работе координаты этих центров е0 получены как случайные числа, равномерно распределенные в прямоугольнике возможных координат исходных точек в диапазонах [xmin, xmax] и [ymin, ymax] соответственно. Затем для каждого объекта кластеризации выбирается ближайшая из этих точек, таким образом получается начальное случайное разбиение на непересекающиеся подмножества S0.
выбирается произвольным образом, например так: из всего множества координат объектов выбираются минимальное и максимальное число по x и по y, затем в этом диапазоне выбираются k точек (начальных центров кластеров). В данной работе координаты этих центров е0 получены как случайные числа, равномерно распределенные в прямоугольнике возможных координат исходных точек в диапазонах [xmin, xmax] и [ymin, ymax] соответственно. Затем для каждого объекта кластеризации выбирается ближайшая из этих точек, таким образом получается начальное случайное разбиение на непересекающиеся подмножества S0.
Для проверки устойчивости результатов и получения различных зависимостей менялся выбор е0, получались 100 различных реализаций, из них выбиралась наилучшая, а также усреднялись полученные параметры для построения различных графиков.
Исследование алгоритма k-means pro
 Разработана программа, реализующая приведенный алгоритм с возможностью визуализации получаемых кластеров и вычисления разнообразных параметров. Для сравнения взят классический алгоритм k-means Мак-Куина [6, 9, 10]. Сравнение производилось на тестовых выборках точек, распределенных равномерно на плоскости. На рисунке 2 показаны кластеры, полученные классическим k-means, а на рисунке 3 – алгоритмом k-means pro. В данном примере железнодорожная магистраль представлена в виде синусоиды (+ отмечены центры кластеров, o – железнодорожные станции). Из рисунков 2 и 3 следует, что оптимальное разбиение точек на кластеры для обычного алгоритма приводит к тому, что центры располагаются произвольно (рис. 2), в то время как с использованием алгоритма k-means pro оптимальная кластеризация допускает только центры, лежащие на железнодорожных станциях (рис. 3).
Разработана программа, реализующая приведенный алгоритм с возможностью визуализации получаемых кластеров и вычисления разнообразных параметров. Для сравнения взят классический алгоритм k-means Мак-Куина [6, 9, 10]. Сравнение производилось на тестовых выборках точек, распределенных равномерно на плоскости. На рисунке 2 показаны кластеры, полученные классическим k-means, а на рисунке 3 – алгоритмом k-means pro. В данном примере железнодорожная магистраль представлена в виде синусоиды (+ отмечены центры кластеров, o – железнодорожные станции). Из рисунков 2 и 3 следует, что оптимальное разбиение точек на кластеры для обычного алгоритма приводит к тому, что центры располагаются произвольно (рис. 2), в то время как с использованием алгоритма k-means pro оптимальная кластеризация допускает только центры, лежащие на железнодорожных станциях (рис. 3).
Разработанный алгоритм применен для решения задачи оптимального выбора мест расположе- ния КП для заданных 900 производств и 137 железнодорожных станций Приволжского федерального округа (ПФО). Производства определялись географическими координатами и объемом контейнеропригодной продукции. Множество железнодорожных станций задано на сети 7 железных дорог, расположенных на территории ПФО. Результат при k = 42 показан на рисунке 4, где точками изображены заданные производства, малыми квадратиками – железнодорожные станции, большими квадратами – найденные станции-КП. Показаны кластеры производств.

Представляет интерес соотношение показателей качества кластеризации для обычного алгоритма и алгоритма кластеризации с проекцией. В первом случае центры кластеров определяются исключительно из свойств расположения объектов (точек) и критерия оптимальности кластеризации D. Такую кластеризацию в контексте данной работы можно назвать свободной.
В рассматриваемом случае центры кластеров обязательно должны находиться на железнодорожной линии, и это является ограничением для самого процесса кластеризации. Алгоритм каждый раз проектирует центры кластеров на железнодорожную линию. В результате получаем вариант кластеризации с проекцией и, очевидно, с другим значением критерия Dпр.
Для классического алгоритма k-means
 ,
,
 .
.
Для k-means pro

 .
.
 На рисунке 5 изображена зависимость D и Dпр от k для вышеприведенного примера, а на рисун- ке 6 для ПФО. Видно, что суммарное расстояние сначала резко падает при увеличении числа кластеров, а затем меняется слабо.
На рисунке 5 изображена зависимость D и Dпр от k для вышеприведенного примера, а на рисун- ке 6 для ПФО. Видно, что суммарное расстояние сначала резко падает при увеличении числа кластеров, а затем меняется слабо.
Назовем дефектом проекции разницу критериальных величин качества свободной кластеризации и кластеризации с проекцией: Δ = Dпр – D. Зависимость Δ /D от k для производств ПФО показана на рисунке 7.
Из графика видно, что при значительном увели- чении числа КП растет дефект проекции, то есть в некоторых случаях, когда разница существенна, возможно, выгоднее строить КП на новых станциях, а не размещать их в существующей инфраструктуре. Вышеприведенные графики дают возможность количественно оценить такие варианты.
Выбор оптимального количества кластеров
Выбор оптимального числа кластеров является проблемным вопросом кластерного анализа [5, 7]. Рассмотрим экономический подход к выбору оптимального количества кластеров k. В данном случае это число определяет количество логистических центров (КП).
Итак, пусть количество КП не задано (k неизвестно), но известна приведенная к одному году нормативная стоимость затрат на создание одно- го КП – с. Тогда в качестве критерия оптимиза- ции при кластеризации нужно взять величину общих затрат на перевозку плюс затраты на созда- ние КП:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 – затраты на перевозку; Di – расстояние от точки-производства до КП; Vi – объем производства контейнеропригодной продукции i-го производства; s – тариф на перевозку 1 тонно-километра.
– затраты на перевозку; Di – расстояние от точки-производства до КП; Vi – объем производства контейнеропригодной продукции i-го производства; s – тариф на перевозку 1 тонно-километра.
Поскольку первое слагаемое в (1) уменьшается при увеличении k, а второе увеличивается от k, величина E имеет минимум, который и определяет оптимальное k при условии, что эта величина попадает в интервал, определяемый ограничениями (2) и (3). На рисунке 8 показаны возможные случаи решения оптимизационной задачи (1), (2), (3). Очевидно, что ограничения (2) и (3) существенно влияют на выбор оптимального k.
 Если объем V такой, что выделенных денег не хватает, то нет никакого решения задачи проектирования сети КП (рис. 8а). Если объем V очень мал и выделенных средств хватает на создание необходимого количества КП, то оптимальное k находится так, как показано на рисунке 8б (минимум обозначен кружком). Здесь оптимальная точка определяется ограничением (2). Рисунок 8в показывает выбор оптимального k, когда объем грузов очень большой, но выделяемых на создание КП средств хватает. Здесь оптимальная точка определяется ограничением (3). На рисунке 8г показан выбор оптимального k, когда объем грузов невелик, а средств на создание КП хватает с запасом. Оптимальная точка определяется минимумом (1). Очевидно, что средства A могут быть уменьшены до величины A = ckopt.
Если объем V такой, что выделенных денег не хватает, то нет никакого решения задачи проектирования сети КП (рис. 8а). Если объем V очень мал и выделенных средств хватает на создание необходимого количества КП, то оптимальное k находится так, как показано на рисунке 8б (минимум обозначен кружком). Здесь оптимальная точка определяется ограничением (2). Рисунок 8в показывает выбор оптимального k, когда объем грузов очень большой, но выделяемых на создание КП средств хватает. Здесь оптимальная точка определяется ограничением (3). На рисунке 8г показан выбор оптимального k, когда объем грузов невелик, а средств на создание КП хватает с запасом. Оптимальная точка определяется минимумом (1). Очевидно, что средства A могут быть уменьшены до величины A = ckopt.
Рассмотрим результаты оптимизации количества КП по критерию E для ПФО в виде графика зависимости общих затрат от k при различных с.
 На рисунке 9 изображены кривые затрат на проект E: Eпр1 (c = 1,5 млн руб.), Eпр2 (c = 5 млн руб.), Eпр3 (c = 12 млн руб.), s = 8 руб./т-км. Из графика видно, что, например, для с = 12 млн руб. оптимальным решением будет создание 15 КП.
На рисунке 9 изображены кривые затрат на проект E: Eпр1 (c = 1,5 млн руб.), Eпр2 (c = 5 млн руб.), Eпр3 (c = 12 млн руб.), s = 8 руб./т-км. Из графика видно, что, например, для с = 12 млн руб. оптимальным решением будет создание 15 КП.
В предложенной методике оптимальное количество КП зависит от величины с. Эта величина является, во-первых, нормативной, то есть усредненной и зависящей от даты проектирования, во-вторых, приведенной, так как увязывает текущие затраты Е1 и капитальные (единовременные) затраты сk. Как известно, это связано также с необходимостью оценки срока окупаемости КП. Все это показывает, что оптимизация числа k возможна только при тщательной экспертной оценке величины c.
Заключение
Полученные результаты показывают возможность и порядок расчетов различных вариантов постановок задач оптимизации размещения транспортных объектов на основе применения алгоритмов кластерного анализа. Разработанный алгоритм k-means pro и программные средства его реализации показали высокую эффективность при решении прикладных задач. Созданные программные средства применены для решения задач проектирования инфраструктуры перевозок на примере ПФО. Предложенные в статье модели, алгоритм и программы позволят лицам, принимающим решения, количественно оценить оптимальные и подоптимальные варианты в конкретных условиях проектирования при оптимизации количества терминальных объектов и мест их размещения.
Литература
1. Кириллова А.Г. Оптимальный выбор расположения терминала как логистического центра при организации контейнерных и контрейлерных перевозок // Транспорт: наука, техника, управление. 2010. № 10. С. 22–25.
2. Москвичев О.В. Модели, методы и алгоритмы оптимизации контейнерно-транспортной системы железнодорожного транспорта на основе кластерного подхода // Транспорт Урала. 2017. № 2. С. 36–60.
3. Михалевич B.C., Трубин В.А., Шор Н.З. Оптимизационные задачи производственно-транспортного планирования. М.: Наука, 1986. 260 с.
4. Есипов Б.А., Москвичев О.В., Складнев Н.С., Алешинцев А.О. Разработка и исследование алгоритма кластеризации с проекцией для решения задач оптимизации транспортной инфраструктуры // Перспективные информационные технологии: тр. Междунар. науч.-технич. конф. Самара: Изд-во СамНЦ РАН, 2017. С. 633–637.
5. Мандель И.Д. Кластерный анализ. М.: Финансы и статистика, 1988. 177 с.
6. Прикладная статистика. Классификация и снижение размерности; [под ред. С.А. Айвазяна]. М.: Финансы и статистика, 1989. 607 с.
7. Миркин Б.Г. Методы кластер-анализа для поддержки принятия решений: обзор: препр. WP7/2011/03. М.: Изд-во ВШЭ, 2011. 88 с.
8. Бериков В.Б., Лбов Г.С. Современные тенденции в кластерном анализе. Н.: Изд-во Ин-та матем. им. С.Л. Соболева СО РАН, 2009. С. 16–21.
9. MacQueen J. Some methods for classification and analysis of multivariate observations. Proc. 5th Berkeley Symp. on Math. Statistics and Probability, 1967, pp. 281–297.
10. Arthur D. and Vassilvitskii S. How Slow is the k-means Method? Proc. 2006 Symp. on Comp. Geometry (SoCG), ACM Press., pp. 144–153.


 ,
,
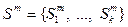 .
. , то есть
, то есть  ,
, ; ni – количество точек i-го кластера.
; ni – количество точек i-го кластера. .
. то есть
то есть
 не возрастает, причем F(Sm) = F(Sm+1), только если Sm=Sm+1, для любого начального разбиения S0 алгоритм через конечное число шагов заканчивает работу. Сложность вычислений по этому алгоритму оценивается как O(nkm), где n – количество кластеризуемых объектов; k – количество кластеров; m – количество итераций.
не возрастает, причем F(Sm) = F(Sm+1), только если Sm=Sm+1, для любого начального разбиения S0 алгоритм через конечное число шагов заканчивает работу. Сложность вычислений по этому алгоритму оценивается как O(nkm), где n – количество кластеризуемых объектов; k – количество кластеров; m – количество итераций.

 ,
, .
.
 .
.
 (1)
(1) (2)
(2) (3)
(3) – затраты на перевозку; Di – расстояние от точки-производства до КП; Vi – объем производства контейнеропригодной продукции i-го производства; s – тариф на перевозку 1 тонно-километра.
– затраты на перевозку; Di – расстояние от точки-производства до КП; Vi – объем производства контейнеропригодной продукции i-го производства; s – тариф на перевозку 1 тонно-километра.

