Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Ключевое слово: |
|
| Page views: 9337 |
Print version Full issue in PDF (1.30Mb) |
Развитие авиационной и ракетной техники возможно только в условиях существенного снижения их веса. Этого можно достичь, в частности, за счет внедрения тонкостенных конструкций. Однако чем тоньше элемент конструкции, тем в большей мере проявляется его способность к выпучиванию и потере устойчивости при сжатии, что часто может сопровождаться появлением пластических деформаций. Поэтому исследование процессов выпучивания и потери устойчивости упругопластических систем весьма актуально.
Задача решается методом конечных элементов (КЭ) как пространственная задача теории пластичности с учетом геометрической нелинейности и больших деформаций. Для ее решения сконструирован пространственный восьмиузловой изопараметрический КЭ (рис. 1). Рассматриваемый КЭ описывается классом CBrick. В нем хранятся координаты узлов и функции для обработки механических характеристик материала. В состав класса CBrick входят восемь объектов класса CGaussPoint. Класс CGaussPoint содержит описание модели гауссовой точки, которая является полным аналогом материальной частицы в механике деформируемого твердого тела. Создание этого класса вызвано тем, что численное интегрирование производится именно в гауссовых точках. В свою очередь каждая гауссова точка (каждый объект класса CGaussPoint) содержит в себе шесть объектов класса CSpace, по числу компонент тензора напряжений Математическое ядро программы реализовано в классе CNumInt. Интерфейс класса составляют функции по вычислению тензоров напряжений и деформаций, векторы внутренних сил, векторы узловых перемещений, функции, реализующие процедуру численного интегрирования, а также решение системы линейных алгебраических уравнений методом LU-факторизации по схеме Холецкого. Для реализации всех этих функций разработаны дополнительные утилиты по обращению матриц, вычислению их определителей и отслеживанию их вырожденности. Решение задачи выпучивания упругопластических систем сводится к решению системы существенно нелинейных алгебраических уравнений. Она решается по шагам, на каждом из которых реализуется итерационный процесс. Процесс итераций на каждом шаге продолжается до тех пор, пока разность результатов на i-й и i+1-й итерации превышает некоторую наперед заданную величину
|
| Permanent link: http://swsys.ru/index.php?id=446&lang=en&page=article |
Print version Full issue in PDF (1.30Mb) |
| The article was published in issue no. № 4, 2006 |
Perhaps, you might be interested in the following articles of similar topics:
- Формирование программ развития больших систем административно-организационного управления
- Методы и средства моделирования wormhole сетей передачи данных
- Интеллектуальная поддержка реинжиниринга конфигураций производственных систем
- Гибридная система поиска решений на основе временных продукционных правил
- Макроэкономическая балансовая модель для стран с элементами переходной экономики
Back to the list of articles
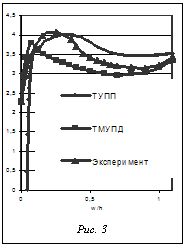 В статье приведено описание программного комплекса для исследования процессов выпучивания и потери устойчивости упругопластических систем и сравнение полученных результатов с экспериментальными данными по двухосному сжатию пластин для оценки достоверности полученного решения. В основу решения положены современная концепция устойчивости упругопластических систем В.Г. Зубчанинова и теория устойчивости упругопластических пластин и оболочек при сложном нагружении на основе теории упругопластических процессов А.А. Ильюшина [2].
В статье приведено описание программного комплекса для исследования процессов выпучивания и потери устойчивости упругопластических систем и сравнение полученных результатов с экспериментальными данными по двухосному сжатию пластин для оценки достоверности полученного решения. В основу решения положены современная концепция устойчивости упругопластических систем В.Г. Зубчанинова и теория устойчивости упругопластических пластин и оболочек при сложном нагружении на основе теории упругопластических процессов А.А. Ильюшина [2].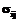 и тензора деформаций
и тензора деформаций 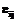 (i,j=1,2,3). В объектах этого класса хранятся прогнозируемые и истинные значения компонент тензоров напряжений и деформаций и их приращения, а также механические характеристики материала. На языке UML описанное агрегирование выглядит в виде диаграммы классов (рис. 2).
(i,j=1,2,3). В объектах этого класса хранятся прогнозируемые и истинные значения компонент тензоров напряжений и деформаций и их приращения, а также механические характеристики материала. На языке UML описанное агрегирование выглядит в виде диаграммы классов (рис. 2).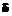 . После достижения требуемой точности делается следующий шаг. В качестве итоговых результатов пользователь получает полную картину напряженно деформируемого состояния на всем протяжении процесса нагружения во всех точках упругопластической системы.
. После достижения требуемой точности делается следующий шаг. В качестве итоговых результатов пользователь получает полную картину напряженно деформируемого состояния на всем протяжении процесса нагружения во всех точках упругопластической системы.