Software & Systems

В последние годы широко применяются такие устройства, как квадрокоптеры и беспилотные летательные аппараты (БПЛА) – дроны, активно используемые для съемки на малых высотах. Они находят применение в сфере удаленного мониторинга объектов и в обследовании сооружений, а также при оценке состояния земель. Одной из их задач является формирование панорамных снимков – высокодетализированных изображений местности, которые зачастую невозможно получить в виде цельной фотографии [1].

Создание композитного снимка из последовательных изображений, полученных с БПЛА, является частным случаем построения панорамного снимка из набора произвольных изображений заданной местности. Условия задачи таковы, что необходимо построить последовательность планарных изображений в соответствии с траекторией полета БПЛА. Линейка БПЛА представлена широким классом устройств с различными летными и нагрузочными характеристиками, причем, чем ниже такие характеристики, тем БПЛА более подвержен влиянию воздушных потоков, что приводит к сложным условиям съемки, а в результате к получению размытых кадров. Напротив, бюджетная легковесная съемочная аппаратура означает получение изображений низкого разрешения. Разрабатываемый алгоритм включает отбор изображений,  их локальное совмещение, глобальное выравнива- ние сцены и устранение визуальных артефактов в местах сшивки, что позволяет устранить указанные недостатки.

Метод создания панорамного аэрофотоснимка

Сведения о траектории полета БПЛА позволяют определить, какие изображения должны быть задействованы на текущем этапе создания панорамного снимка (рис. 1). Примем, что моменты начала и окончания съемки с целью получения панорамного снимка указываются пользователем. Строится граф пронумерованных изображений, и на текущем этапе создания панорамного снимка используются все имеющиеся соседние изображения. Такая процедура позволяет избавиться от дорогостоящего сопоставления случайных пар неотсортированных изображений [2].

Также следует проводить обязательную проверку на размытость изображений для ее устранения или удаления размытого изображения из набора сшиваемых изображений (при сильной степени размытости). В работе [3] предложен усовершенствованный метод устранения размытия, позволяющий оценивать четкость изображения на основе градиентной информации по всему текущему изображению относительно имеющихся изображений и заданному порогу размытия. Нахождение границ объектов на изображении выполняется оператором Собела. Для детализированных регионов следует применять анизотропный фильтр Гаусса для сглаживания негативных эффектов размытия, при этом сохраняя информацию о границах в неизменном виде. Используется анизотропный фильтр Гаусса с переменным ядром. Для гладких регионов применяется алгоритм нерезкого маскирования, основанный на вычитании размытого изображения из четкого изображения. В результате формируется изображение с частично или полностью устраненными эффектами размытия.

Совмещение изображений, которые в общем случае получены при различных углах наклона камеры, является одной из основных процедур создания панорамного снимка. Известны два основных подхода: непосредственное совмещение изображений и совмещение с использованием точечных дескрипторов [4]. Считается, что первый подход обеспечивает большую точность совмещения, однако имеет ограничения по параметрам съемки (они должны быть практически такими же, как параметры съемки исходного снимка). Более общим является подход на основе точечных дескрипторов (Speeded-Up Robust Feature (SURF) [5], Features from Accelerated Segment Test (FAST) [6], FAST Enhanced Repeatability (FAST-ER)) или стабильных областей (Affine Invariant Intensity Extrema, Maxi- mally Stable Extremal Region (MSER)) [7]. В таком случае формирование панорамных изображений будет включать следующие основные этапы: обнаружение особых точек кадров видеопоследовательности и формирование наборов точечных особенностей, сопоставление этих наборов, построение проективного преобразования для выравнивания изображений и их переноса в общую плоскость, непосредственная сшивка выровненных изображений.

Помимо классических подходов, в последние годы развиваются быстрые методы построения панорамных снимков, например, основанные на расширенном фильтре Калмана и методе одновременной локализации и сопоставления (Simultaneous Localization and Mapping (SLAM)) [8].

В данной работе параллельно рассчитываются быстрые дескрипторы FAST и FAST-ER [9], предназначенные для обнаружения углов, и дескриптор SURF, учитывающий фактор масштабирования. Данные алгоритмы могут применяться для решения проблемы вычислительной сложности слияния изображений. В дескрипторе FAST проверяется, является ли пиксел p углом, путем сравнения значения его яркости со значениями яркостей 16 пикселов {x1, x2, …, x16} с радиусом 3 вокруг проверяемого пиксела p (рис. 2).

Для ускорения работы алгоритма вначале рас- сматриваются пикселы с номерами 1, 5, 9 и 13. Если, по крайней мере, три из четырех пикселов удовлетворяют пороговому критерию, пиксел p считается углом. Если хотя бы три из четырех значений находятся ниже порогового значения Ip + TFAST, пиксел p не является точкой интереса и отбрасывается. В противном случае проверяются все 16 значений окружающих пикселов в виде вектора Sp®x, принимающего соответственно темное, подобное и светлое значения в соответствии со следующим выражением:

   (1)

где Ix – яркость пиксела на окружности вокруг проверяемого пиксела; Ip – яркость проверяемого пиксела; TFAST – пороговое значение для дескриптора FAST, например, 20 % значения яркости.

Далее строятся подмножества Pd, Ps, Pb и определяется переменная Kp, которая в соответствии с классификатором дерева решений [10] определяет, является ли проверяемый пиксел углом или нет. Для снижения влияния шумов на результат работы алгоритма перед его применением рекомендуется произвести размытие изображения фильтром Гаусса.

Для идентификации особой точки в дескрипторе SURF строится массив из 64 (в расширенной версии 128) чисел. При этом размер окна для поиска дескриптора равен 20s, где s – масштаб, в котором была найдена особая точка. Дескриптор содержит описание градиентов для 16 квадрантов вокруг особой точки. Далее квадрат разбивается на 16 более мелких квадрантов. В каждом квадранте берется регулярная сетка 5×5, и для каждой точки сетки ищется градиент с помощью фильтра Хаара. Размер фильтра Хаара берется равным 2s и для первой октавы составляет 4×4. Следует отметить, что при расчете фильтра Хаара изображение не поворачивается и фильтр рассчитается в обычных координатах изображения. Затем полученные координаты градиента (dX, dY) поворачиваются на угол, соответствующий ориентации квадрата. На рисунке 3 представлен пример обнаружения особых точек на изображении с применением алгоритмов FAST, FAST-ER и SURF [11].

Также для описания точки используется знак следа матрицы Гессе. Для светлых точек на темном фоне след отрицательный, а для темных точек на светлом фоне след положительный. Таким образом, SURF различает светлые и темные пятна.

Одним из самых распространенных способов оценки параметров модели является алгоритм RANSAC (RANdom SAmple Consensus) [12]. Концепция данного алгоритма основана на разделении всех исходных данных на выбросы (outliers) и попадания (inliers). Выбросами являются ложные точки, шумы, случайные включения в исходные данные, то есть такие точки, на основании которых нельзя построить требуемую модель. Попадания – это точки, удовлетворяющие модели. Данный алгоритм выполняется итеративно. У алгоритма RANSAC имеется ряд недостатков, которые иногда не позволяют получить требуемый результат за приемлемое время, так как отсутствует верхняя граница времени, необходимого для вычисления параметров модели. В настоящее время разработаны, реализованы и протестированы модификации данного алгоритма. Одной из них является алгоритм MLESAC [13]. Данный алгоритм вычисляет вероятность гипотезы, представляя распространение ошибки как смешивание моделей. Для одновременного вычисления параметров модели и доли выбросов применяется схема максимизации ожидания. Для сшивки изображений требуется подобрать четыре наилучших сопоставления точечных особенностей, координаты которых используются для вычисления коэффициентов матрицы гомографии:

,                                      (2)

 где h1, …, h9 – коэффициенты матрицы; (xi, yi) и (xj, yj) – координаты соответствующих точек.

При проективном преобразовании, h9 = 1, выражение (2) принимает вид

.     (3)

Тогда пара соответствующих точек связана следующими соотношениями:

               (4)

Сшивка изображений на основе матриц гомографии позволяет осуществлять локальное выравнивание панорамного снимка. Для глобального выравнивания должны одновременно использоваться все матрицы гомографии, что невозможно выполнить в реальном времени. В этом случае можно воспользоваться частичным выравниванием сшитых изображений на основе аффинных преобразо- ваний с использованием метода наименьших квад- ратов или применить эвристические алгоритмы поиска геометрических примитивов с артефактами сшивки для последующего выравнивания.

Бесшовное смешивание изображений, как правило, является необходимым после построения панорамного снимка в связи с возникающими локальными артефактами освещенности, рассогласования текстурной мозаики и т.д. Известны четыре категории методов, а именно: дискретные цветовые методы, методы на основе построения пирамиды изображений, градиентные методы и многополосное смешивание [14]. Многополосное смешивание относится к высокоэффективным, но наиболее затратным методам устранения артефактов сшивки. Идея метода, предложенного в [15], заключается в смешивании низких частот по большому пространственному диапазону, а высоких частот – по малому пространственному диапазону. Результатом многополосного смешивания является суммирование изображений по всем поддиапазонам.

Описание экспериментального исследования

Для проведения экспериментов использовался набор изображений Swiss dataset [16], полученный дроном eBee RTK, имеющим следующие характеристики: масштаб – 4 см/пикс., область – 0,18 км2, высота полета – 169 м, число изображений – 32. Пример создания панорамного аэрофотоснимка на основе многополосного смешивания для набора из 32 изображений представлен на рисунке 4.

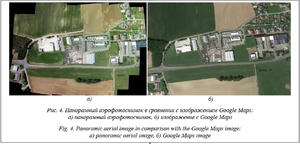
Тестирование проводилось на компьютере со следующей конфигурацией: процессор AMD Athlon II X3 3.2GHz, оперативная память 8GB DDR3 1333Mhz, видеокарта NVIDIA GeForce GTX 650. В таблице 1 представлено время работы алгоритма нахождения особых точек, преобразования и сопоставления изображений с разным разрешением при использовании алгоритмов FAST, FAST-ER и SURF. Сравнение времени работы алгоритмов расчета матрицы гомографии при сопоставлении изображений с разрешением 1280×720 пикселов приведено в таблице 2.

Таблица 1

Время работы алгоритма сопоставления изображений (мс)

Table 1

The execution time of image matching algorithm (ms)

Таблица 2

Сравнение времени работы (мс) алгоритмов RANSAC и MLESAC

Table 2

Comparison of the operating time of RANSAC and MLESAC algorithms (ms)

Проведенные исследования показали, что использование алгоритма MLESAC позволяет повысить точность сопоставления особых точек в среднем на 5 % по сравнению с алгоритмом RANSAC, при этом скорость работы алгоритма уменьшается в среднем на 15 %.

Заключение

Применение алгоритмов FAST и FAST-ER позволяет организовать сопоставление изображений (с разрешением до 1920×1080 пикселов) для формирования панорамного снимка в реальном режиме времени, а слияние изображений с применением технологии многополосного смешивания обеспечивает качественную визуализацию в местах сшивки. Основным недостатком рассмотренных алгоритмов является использование в расчетах яркостной составляющей пиксела, что может приводить к некорректным результатам сшивки при наличии на изображениях областей с повышенной яркостью или больших фрагментов, содержащих блики.

Работа выполнена при финансовой поддержке РФФИ, грант № 16-07-00121 А.

Литература

1.     He K., Chang H., Sun J. Rectangling panoramic images via warping. Proc. Conf. ACM Transactions on Graphics – SIGGRAPH, 2013, vol. 32, i. 4, art. 79.

2.     Bold S., Sosorbaram B., Lee S.R. Implementation of autonomous unmanned aerial vehicle with moving-object detection and face recognition. Information Science and Applications (ICISA). 2016, vol. 376, pp. 361–370.

3.     Буряченко В.В., Фаворская М.Н., Зотин А.Г., Пахир- ка А.И. Восстановление границ кадра при стабилизации на основе построения модели фона и оценки значимости объектов // Информационно-управляющие системы. 2017. № 5. С. 42–51.

4.     Leutenegger S., Chli M., Siegwart R.Y. BRISK: Binary robust invariant scalable keypoints. Proc. IEEE Intern. Conf. Computer Vision (ICCV), 2011, pp. 2548–2555.

5.     Bay H., Ess A., Tuytelaars T., van Gool L. Speeded-up robust features (SURF). Computer Vision and Image Understanding. 2008, vol. 110, no. 3, pp. 346–359.

6.     Lowe D.G. Distinctive image features from scale-invariant keypoints. Intern. J. of Computer Vision. 2004, vol. 60, no. 2, pp. 91–110.

7.     Tuytelaars T., van Gool L.J. Matching widely separated views based on affine invariant regions. Intern. J. of Computer Vision. 2004, vol. 59, no. 1, pp. 61–85.

8.     Civera J., Davison A.J., Magallón J.A., Montiel J.M. Drift-free realtime sequential mosaicing. Intern. J. of Computer Vision. 2009, vol. 81, no. 2, pp. 128–137.

9.     Зотин А.Г., Пахирка А.И., Дамов М.В. Сравнение алгоритмов получения точечных особенностей для системы сопоставления кадров видеопоследовательности // Региональные проблемы дистанционного зондирования Земли: матер. IV Междунар. науч. конф. 2017. С. 112–115.

10.   Quinlan J.R. Induction of decision trees. Machine Learning. 1986, vol. 1, pp. 81–106.

11.   Rublee E., Rabaud V., Konolige K., Bradski G. ORB: an efficient alternative to SIFT or SURF Proc. IEEE Intern. Conf. Computer Vision (ICCV), 2011, pp. 2564–2571.

12.   Fischler M.A., Bolles R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applica-tions to Image Analysis and Automated Cartography. Communications of the ACM, 1981, vol. 24, no. 6, pp. 381–395.

13.   Torr P.H.S., Zisserman A. MLESAC: A New Robust Estimator with Application to Estimating Im-age Geometry. Computer Vision and Image Understanding, 2000, vol. 78, pp. 138–156.

14.   Favorskaya M.N., Buryachenko V.V., Zotin A.G., Pakhir- ka A.I. Video completion in digital stabili-zation task using pseudo-panoramic technique. Proc. 2nd International ISPRS, 2017, pp. 83–90.

15.   Burt P.J., Adelson E.H. A multiresolution spline with application to image mosaics. ACM Transac-tions on Graphics, 1983, vol. 2, no. 4, pp. 217–236.

16.   Example Datasets. URL: https://www.sensefly.com/drones/ example-datasets.html (дата обращения: 14.11.2017).