Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (rgordeev@naumen.ru) - , Russia, Ph.D, () - | |
| Ключевое слово: |
|
| Page views: 10645 |
Print version Full issue in PDF (1.30Mb) |
В моделях принятия решений зачастую приходится решать задачи оптимизации. В некоторых из них условия на допустимое множество задаются в лингвистической форме. Например, инвестор желает получить прибыль с вероятностью не ниже некоторого заранее оговоренного уровня. Это приводит к формулировке оптимизационной задачи с вероятностными ограничениями [1]. Однако при решении подобных задач зачастую мы не знаем априори распределения вероятностей в тех или иных ситуациях и вынуждены вместо них использовать некоторые приближения или оценки. Для оценивания подобных приближений пользуются методами теории устойчивости или анализа возмущений, приложение которых и рассмотрено в настоящей статье для класса задач, определенного соотношением (1). Рассмотрим следующую задачу оптимизации с вероятностными ограничениями
Здесь Последнее предположение означает, что
верно для всех Функцию распределения, соответствующую вероятностной мере
Однако в большинстве случаев известна лишь частичная информация о
И если получена достаточно хорошая аппроксимация v меры Хотя предполагается, что исходная задача выпукла, однако не следует делать предположений о возмущенной задаче (3). Это позволяет рассмотреть класс эмпирических аппроксимаций, которые не обладают свойствами выпуклости или гладкости. И поскольку в общем случае задача (3) предполагает не единственное решение в условиях предположений (2), рассмотрим множества решений. Зависимость решений и оптимальных значений от параметра v описывается точечно множественным отображением
Рассмотрим условия, наложенные на исходную задачу (1), при которых
Качественная устойчивость задачи (1) предполагает, что Помимо качественной устойчивости огромный интерес представляет вопрос количественной устойчивости. Напомним, что
для всех Существует прямая связь между непрерывностью по Хаусдорфу-Гельдеру с показателем k отображения множества решений и экспоненциальными границами эмпирических приближений решения [2]. И отклонения эмпирических аппроксимаций от множества решений исходной задачи может быть оценено при помощи экспоненциальных границ [2,3]. Сформулируем утверждение, которое дает достаточные условия устойчивости оптимальных значений возмущенной задачи. Теорема 1. В дополнение к условиям (2) пусть выполнены следующие положения для фиксированной вероятностной меры 1. 2. Существует Тогда Заметим, что в теореме 1 липшицева оценка для Для формулировки условий устойчивости множества решений введем следующие объекты, где
Заметим, что Сформулируем результат, позволяющий определить устойчивость множества оптимальных решений задачи (3). Теорема 2. В дополнение к условиям (2) пусть выполнены следующие предположения для некоторой фиксированной меры 1. 2. Существует 3. 4. Тогда
Первое предположение теоремы 2 носит чисто технический характер и может быть усилено, например, компактностью множества X. Второе может быть интерпретировано как условие Слейтера. В некоторых случаях его можно проверить, не зная в явном виде меры Список литературы 1. Prekopa, A. Stochastic Programming. Kluwer, Dordrecht, 1995. 2. Henrion, R., Romisch, W. Metric regularity and quantitative stability in stochastic programs with probability constraints. Math. Program. 84, 55-88 (1999). 3. Henrion, R., Romisch, W. Stability of solutions to chance constrained stochastic programs. In: (J. Guddat, R. Hirabayashi, H.Th. Jongen and F. Twilt eds.) Parametric optimization and Related Topics V, Peter Lang, Frankfurt a.M. 2000, pp. 95-114. |
| Permanent link: http://swsys.ru/index.php?id=447&lang=en&page=article |
Print version Full issue in PDF (1.30Mb) |
| The article was published in issue no. № 4, 2006 |
Perhaps, you might be interested in the following articles of similar topics:
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
- Компьютер - хранитель домашнего очага
- Системы баз данных и знаний, разработанные в Республике Куба
- Сравнение сложных программных систем по критерию функциональной полноты
Back to the list of articles
 . (1)
. (1) – s-мерный случайный вектор, определенный на вероятностном пространстве
– s-мерный случайный вектор, определенный на вероятностном пространстве  ;
;  – целевая функция;
– целевая функция;  – некоторое множество;
– некоторое множество;  система ограничений неравенств;
система ограничений неравенств;  – некоторый заданный уровень вероятности. Заданные ограничения по вероятности означают, что неравенство
– некоторый заданный уровень вероятности. Заданные ограничения по вероятности означают, что неравенство  должно быть выполнено с вероятностью не ниже p. Наиболее очевидным представляется задать ограничения в виде системы линейных неравенств, то есть
должно быть выполнено с вероятностью не ниже p. Наиболее очевидным представляется задать ограничения в виде системы линейных неравенств, то есть  , где A – некоторая матрица. Обозначим через
, где A – некоторая матрица. Обозначим через  (борелево пространство вероятностных мер, определенных на
(борелево пространство вероятностных мер, определенных на  ) распределение вероятностей случайного вектора
) распределение вероятностей случайного вектора  . Сделаем некоторые предположения о выпуклости рассматриваемой проблемы: g выпукла, X замкнуто и выпукло, компоненты h вогнуты и вероятностная мера
. Сделаем некоторые предположения о выпуклости рассматриваемой проблемы: g выпукла, X замкнуто и выпукло, компоненты h вогнуты и вероятностная мера  является
является  -вогнутой для некоторого
-вогнутой для некоторого  .
. является выпуклой функцией множеств, то есть
является выпуклой функцией множеств, то есть (2)
(2) и всех измеримых по Борелю и выпуклых множеств
и всех измеримых по Борелю и выпуклых множеств  , таких что
, таких что  также измеримо по Борелю. Заметим, что большинство многомерных распределений являются r-вогнутыми для некоторого
также измеримо по Борелю. Заметим, что большинство многомерных распределений являются r-вогнутыми для некоторого  , таким образом задачу (1) можно переписать следующим образом:
, таким образом задачу (1) можно переписать следующим образом: .
. , являющейся оценкой для
, являющейся оценкой для  . Обычно v выбирается как параметрическая или непараметрическая оценка
. Обычно v выбирается как параметрическая или непараметрическая оценка  . (3)
. (3) и расширенно-значной функцией
и расширенно-значной функцией  как
как ,
, .
. и
и 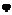 локально устойчивы относительно фиксированной меры
локально устойчивы относительно фиксированной меры  , (
, ( ) и метрикой Колмогорова, определенной на множестве замкнутых подмножеств
) и метрикой Колмогорова, определенной на множестве замкнутых подмножеств  ,
, , (
, ( ).
). при
при  . При определенных условиях это означает, что предельные точки аппроксимирующих решений будут решениями исходной задачи и любое решение исходной задачи будет пределом для последовательности аппроксимирующих решений.
. При определенных условиях это означает, что предельные точки аппроксимирующих решений будут решениями исходной задачи и любое решение исходной задачи будет пределом для последовательности аппроксимирующих решений. в
в  такие, что
такие, что (4)
(4) .
. :
: не пусто и ограничено.
не пусто и ограничено. , такой что
, такой что  .
. и
и  для всех
для всех  ,
,  .
. – открытый шар,
– открытый шар, ,
,
 , (
, ( ),
), , (
, ( ).
). и
и  обозначают соответственно множества решений и оптимальное значение параметрической задачи, ограничивающей решения исходной задачи снизу, а параметр y соответствует правосторонним возмущениям в неравенствах, заданных отображением h. В противоположность многозначная функция Y определяет множество решений параметрической задачи, ограничивающей решения исходной задачи сверху, в которой явные ограничения неравенства заменены условием, наложенным на значения функции распределения
обозначают соответственно множества решений и оптимальное значение параметрической задачи, ограничивающей решения исходной задачи снизу, а параметр y соответствует правосторонним возмущениям в неравенствах, заданных отображением h. В противоположность многозначная функция Y определяет множество решений параметрической задачи, ограничивающей решения исходной задачи сверху, в которой явные ограничения неравенства заменены условием, наложенным на значения функции распределения  . Это позволяет отдельно рассматривать влияние
. Это позволяет отдельно рассматривать влияние  является строго выпуклой в некоторой выпуклой окрестности U отображения
является строго выпуклой в некоторой выпуклой окрестности U отображения  , где
, где  на
на  .
. в
в  ,
, ,
,  является строго выпуклой на ограниченных выпуклых множествах. И последнее предположение теоремы 2 требует Гельдеревой непрерывности
является строго выпуклой на ограниченных выпуклых множествах. И последнее предположение теоремы 2 требует Гельдеревой непрерывности 