Одной из особенностей человеческого интеллекта является возможность принимать решения в условиях неполной информации и неопределенности. Теория вероятностей и теория нечетких множеств представляют в настоящее время основные методологические направления для учета и анализа неопределенностей самой различной природы. На сегодняшний день нечеткие множества находят применение в самых разных научно-технических и социально-экономических областях человеческой деятельности [1, 2].
Нечеткие числа представляют собой важное и востребованное направление в рамках теории нечетких множеств [3–5]. При этом ранжирование нечетких чисел является одной из ключевых проблем теории нечетких множеств [6]. В отличие от действительных чисел нечеткие числа не имеют естественного способа (очевидного и/или основанного на применении интуитивно понятных аксиом) их сравнения и ранжирования. В настоящее время существует более 40 методов ранжирования нечетких чисел [3, 4]. В данной работе реализованы три метода ранжирования с использованием дефаззификации нечетких чисел, а также два метода ранжирования на основе попарного сравнения с применением нечетких отношений предпочтения.
Базовые понятия теории нечетких множеств и нечетких чисел
Нечеткое множество (см. [5, 7]) представляет собой расширение классического понятия множества, в котором функция принадлежности элемента множеству может принимать любые значения в интервале [0, 1].
Определение 1. Нечеткое число (fuzzy number) Z представляет собой выпуклое, нормальное и ограниченное нечеткое множество, определенное на множестве действительных чисел  , с непрерывной или кусочно-непрерывной сверху функцией принадлежности mz(x) Î [0, 1] (см. [5, 7]).
, с непрерывной или кусочно-непрерывной сверху функцией принадлежности mz(x) Î [0, 1] (см. [5, 7]).
Таким образом, предполагается наличие действительных чисел c1, c2, c1 £ c2, таких, что
Z = {(x, mz(x)): mz(x) > 0, x Î (c1, c2),
mz(x) = 0, x Ï [c1, c2]}. (1)
Всюду далее  представляет множество нечетких чисел согласно определению 1.
представляет множество нечетких чисел согласно определению 1.
Замечание 1. Если c1 = c2 = c, Z = c является синглтоном (singleton) и mz(c) = 1.
Замечание 2. Строго говоря, условие mz(c1) = = mz(c2) = 0 не является необходимым и часто используется для удобства, подчеркивая тем самым наиболее используемый в приложениях вид нечетких чисел.
Определение 2. a-срез (a-cut) нечеткого числа Z, a Î (0, 1], представляет собой четкое множество:  (см. [5, 7]).
(см. [5, 7]).
Для a = 0 положим [A0, B0] = [c1, c2] (здесь c1, c2 – граничные значения согласно (1)), тогда нечеткое число Z может быть идентифицировано с множеством a-срезов:
Z = {[Aa, Ba]}, a Î [0, 1]. (2)
Определение 3. Нечеткое отношение предпочтения (fuzzy preference relation) представляет собой бинарное отношение R = ((Zi, Zj), mR(Zi, Zj)), в котором нечеткая мера mR(Zi, Zj) отражает степень предпочтения нечеткого числа Zi над Zj.
Определение 4. Пусть R – нечеткое отношение предпочтения на  ´
´ , тогда для любых нечетких чисел Zi, Zj Î
, тогда для любых нечетких чисел Zi, Zj Î их нечеткое ранжирование определяется следующим образом [8]:
их нечеткое ранжирование определяется следующим образом [8]:
 , если mR(Zi, Zj) ³ 0.5;
, если mR(Zi, Zj) ³ 0.5;
 , если mR(Zi, Zj) > 0.5; (3)
, если mR(Zi, Zj) > 0.5; (3)
Zi ~ Zj, если mR(Zi, Zj) = 0.5.
Ранжирование нечетких чисел
Методы ранжирования нечетких чисел можно разделить на три основные группы [3, 4]:
- методы дефаззификации;
- методы, основанные на оценке расстояния до эталонного множества;
- методы попарного сравнения.
В данной работе рассматриваются методы дефаззификации и попарного сравнения, представляющие собой наиболее востребованные методы ранжирования нечетких чисел.
Метод дефаззификации основан на представлении нечеткого числа A соответствующим методу четким (crisp) значением, заменяющим исходное нечеткое число в последующих оценках. В данной работе используются три метода дефаззификации: метод центра тяжести (Centroid Index или метод Ягера Y1), метод медианы (mA) и метод интеграла средних значений α-срезов (метод Ягера Y2) [3].
Метод центра тяжести. Для нечеткого числа A, определенного на отрезке [c1, c2] (см. определение 1), дефаззификация по методу центра тяжести происходит согласно следующей формуле [3, 9]:
 , (4)
, (4)
где CI(A) представляет собой центроид-индекс. Аналогом CI(A) является математическое ожидание случайной величины, заданной с плотностью распределения вероятностей mA(x)/S, где  (площадь под кривой функции принадлежности) [3, 10].
(площадь под кривой функции принадлежности) [3, 10].
Метод медианы. Медианным значением mA нечеткого множества A, определенного на [c1, c2], называется такое число, для которого справедливо выражение [11]:
 . (5)
. (5)
Геометрически медиана представляет собой такую точку на оси абсцисс, что проведенный через нее перпендикуляр делит площадь плоской фигуры, ограниченной функцией принадлежности нечеткого множества, на две равные части.
Метод интеграла средних значений α-срезов. Для нечеткого числа Z, представленного согласно (2), по методу Ягера Y2 вычисляется следующий интеграл [3]:
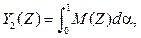 (6)
(6)
где M(Z) – среднее значение a-среза [Aa, Ba]: M(Z) = (Aa + Ba)/2.
Методы попарного сравнения. В рамках системы ранжирования F-Ranking реализованы два метода попарного сравнения, основанные на нечетком анализе приемлемости рангов (Fuzzy Rank Acceptability Analysis, FRAA) с применением интегрального нечеткого отношения предпочтения – FRAAI [8], а также нечеткого отношения предпочтения Юаня [4, 8] – FRAAY.
Интегральное отношение предпочтения RI = = (Zi, Zj, mI(Zi, Zj)) основывается на вычислении площади SI(Zij) под функцией принадлежности нечеткого числа Zij = Zi – Zj = {[Aa, Ba]}, а также площади  под положительной частью (x ³ 0) данной функции принадлежности:
под положительной частью (x ³ 0) данной функции принадлежности:
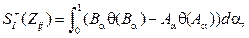 (7)
(7)
где q(x) – функция Хэвисайда: q(x) = {1, x ³ 0; 0, x < 0}.
Степень предпочтения Zi над Zj вычисляется по формуле
 (8)
(8)
(для четких/crisp чисел Zi, Zj, SI(Zij) = 0, для этого случая формула (8) имеет соответствующую естественную модификацию [8, 12]).
Для отношения предпочтения Юаня степень предпочтения Zi над Zj, mY(Zi, Zj), также вычисляется по формуле (8) (с заменой нижнего индекса I на Y), однако  интерпретируется в этом случае как расстояние от положительной части нечеткого числа Zij = Zi – Zj = {[Aa, Ba]} до оси OY и вычисляется по формуле
интерпретируется в этом случае как расстояние от положительной части нечеткого числа Zij = Zi – Zj = {[Aa, Ba]} до оси OY и вычисляется по формуле
 , (9)
, (9)
при этом
 . (10)
. (10)
Нечеткий анализ приемлемости рангов (FRAA; Fuzzy Rank Acceptability Analysis). Рассмотренные выше нечеткие отношения предпочтения использу- ются в нечетком анализе приемлемости ранга для ранжирования нечетких чисел [8, 12]. Метод FRAA базируется на оценке индексов нечеткой приемлемости рангов (Fuzzy Rank Acceptability Indices, FRAIs). Для оценки FRAIs используется модель оценки нечеткой меры утверждения/события ранга (FRS, Fuzzy Rank Statement) Fik [8]: Fik = (Zi, k) = {Zi имеет ранг k}, i, k = 1, …, n.
Нечеткий индекс приемлемости ранга (FRAI) m(i, k) определяется как нечеткая мера утверждения (нечеткого логического выражения) Fik : m(i, k) = = mR(Fik) для заданного отношения предпочтения R (детальное изложение свойств метода FRAA представлено в [12]). Для нечетких чисел Zi, i = 1, …, n, и нечеткого отношения предпочтения R нечеткое число Zm имеет FRAAR ранг k Î {1, …, n}, r(Zm) = k, если Zm имеет максимальный нечеткий индекс приемлемости для ранга k:
mR(m, k) = maxi=1, …, n mR(i, k), 1 £ m, k £ n. (11)
Свойства FRAA-ранжирования на основе отношений предпочтения RI (FRAAI) и RY (FRAAY) исследованы в [12].
Существующие системы ранжирования нечетких чисел
На сегодняшний день существуют различные программные комплексы/системы, использующие нечеткие числа, в которых применяются методы сравнения и ранжирования нечетких чисел. Несмотря на разнообразие алгоритмов ранжирования, в указанных нечетких системах в основном применяются методы дефаззификации. При этом существует лишь несколько систем, непосредственно предназначенных для ранжирования нечетких чисел.
Fuzzy Logic Designer (www.mathworks.com/help/ fuzzy/fuzzylogicdesigner-app.html). Реализованы логические операции над нечеткими множествами со следующими функциями принадлежности: треугольная, трапециевидная, колоколообразная, Гаусса, z-образная и s-образная. Имеется возможность производить ранжирование методами дефаззификации (центр тяжести, среднее максимума, наименьшее максимума, наибольшее максимума); экспорт в систему MATLAB. Программа является платной, доступна демонстрационная 30-дневная версия.
fuzzyTECH (www.fuzzytech.com). Предназначена для решения различных задач нечеткого моделирования; в системе реализованы следующие методы дефаззификации: центр максимума, центр минимума, центр тяжести, среднее максимума.
FUZDYNт. В данной системе реализованы следующие методы: Ченга, Кауфманна и Гупта, Ли и Вонга, Джейна, Дубоиса и Прайда, входящие в две группы методов ранжирования (дефаззификации и попарного сравнения), при этом входными величинами могут быть только треугольные и трапецие- видные нечеткие числа. В [13] представлены входные и выходные формы программы.
Приложение F-Ranking
Созданная система F-Ranking является настольным приложением, разработанным на языке программирования Java (что делает приложение кроссплатформенным, для запуска требуется наличие Java Runtime Environment (JRE) v. 1.8), и может применяться для решения широкого круга задач с использованием нечетких чисел. В приложении реализованы следующие методы ранжирования нечетких чисел на основе дефаззификации и попарного сравнения: метод центра тяжести, метод медианы, метод интеграла средних значений a-срезов, а также методы FRAAI и FRAAY, основанные, соответственно, на нечетких отношениях предпочтения RI (интегральное отношение предпочтения) и RY (отношение предпочтения Юаня), которые также реализованы в системе (см. http://www. swsys.ru/uploaded/image/2018-3/2018-3-dop/28.jpg, http://www.swsys.ru/uploaded/image/2018-3/2018-3-dop/29.jpg и табл. 1). Отношения предпочтения RI и RY используют в своей основе нечеткую меру (степень) предпочтения числа Zi над Zj: mY(Zi, Zj) и mI(Zi, Zj). В то же время в системе F-Ranking фактически реализованы также методы ранжирования, основанные на отношениях предпочтения RY и RI на основе использования мер предпочтения mY(Zi, Zj) и mI(Zi, Zj). В [12] доказано, что ранжирования заданного множества нечетких чисел по методам FRAAY и RY совпадают; однако FRAAY-ранжирование в отличие от ранжирования на основе отношения предпочтения RY дает дополнительную информацию о мере того, что нечеткое число Zk имеет соответствующий ранг m. Показано также (см. [12], табл. 1), что ранжирование RI не является транзитивным.
UML-диаграмма классов, реализующих методы ранжирования нечетких чисел, представлена на рисунке (см. http://www.swsys.ru/uploaded/image/ 2018-3/2018-3-dop/26.jpg).
 При работе с программой пользователь задает нечеткие числа, выбирает методы ранжирования и проводит ранжирование заданного множества или подмножества нечетких чисел (рис. 1).
При работе с программой пользователь задает нечеткие числа, выбирает методы ранжирования и проводит ранжирование заданного множества или подмножества нечетких чисел (рис. 1).
В программе реализованы следующие типы нечетких чисел (по функции принадлежности): синглтоны, треугольные, трапециевидные и кусочно-линейные нечеткие числа (см. http://www.swsys.ru/ uploaded/image/2018-3/2018-3-dop/27.jpg).
Нечеткие числа с нелинейной функцией принадлежности mZ(x) могут быть аппроксимированы кусочно-линейной функцией с достаточной для практического применения точностью.
Ранжирование нечетких чисел может проводиться по всем или по нескольким выбранным (из списка реализованных) методам ранжирования. Окно результатов ранжирования состоит из нескольких вкладок и позволяет сравнить полученные результаты по нескольким методам.
 На первой вкладке (рис. 2) отображаются результаты ранжирования по всем выбранным методам с указанием соответствующего методу ранжирования значения: для методов дефаззификации это значения, полученные в результате дефаззификации исходных чисел, а для методов FRAAI и FRAAY – максимальная, согласно FRAA-ранжированию, нечеткая мера (степень/мера уверенности), что число принадлежит данному рангу.
На первой вкладке (рис. 2) отображаются результаты ранжирования по всем выбранным методам с указанием соответствующего методу ранжирования значения: для методов дефаззификации это значения, полученные в результате дефаззификации исходных чисел, а для методов FRAAI и FRAAY – максимальная, согласно FRAA-ранжированию, нечеткая мера (степень/мера уверенности), что число принадлежит данному рангу.
Для методов попарного сравнения можно также получить значения нечетких индексов приемлемости FRAIs в виде таблицы и графика (рис. 3). Например, при использовании интегрального отношения предпочтения RI нечеткое число Z2 принадлежит рангу 1 с мерой уверенности 0.643 – – mI(2, 1) = 0.643, рангу 2 с мерой 0.357 – mI(2, 2) = = 0.357 и рангу 3 с мерой 0.057 – mI(2, 3) = 0.057.

Кроме того, для всестороннего анализа полученных результатов по методам попарного сравнения RY и RI существует возможность рассмотреть значения меры превосходства mR(Zi, Zj) одного числа над другими (см. http://www.swsys.ru/uploaded/image/2018-3/2018-3-dop/28.jpg).
В программе доступны русский и английский языки (переключение: File>Language). Настройка параметров программы (количество знаков после точки и т.д.) производится в меню File > Settings. Кроме того, имеется возможность сохранить вве- денные нечеткие числа для их повторного использования. Для отображения нечетких чисел на правой панели (рис. 1) используется свободная библиотека jFreeChart.
Примеры использования системы F-Ranking
Представим ряд примеров, иллюстрирующих работу созданной системы с использованием нечетких чисел с функциями принадлежности треугольной, трапециевидной и кусочно-линейной формы и всеми методами ранжирования, реализованными в системе.
Пример 1. Рассмотрим три множества (S1, S2, S3) треугольных нечетких чисел (рис. 4), визуальное/ интуитивное ранжирование которых невозможно:

S1: Z1 = (11, 13.95, 16.91),
Z2 = (13.9, 13.95, 14), Z3 = (10, 14.95, 16.29); (12)
S2: Z1 = (11, 13.95, 16.91),
Z2 = (13.9, 13.95, 14), Z3 = (10, 14.95, 16.3); (13)
S3: Z1 = (11, 13.95, 16.9),
Z2 = (13.9, 13.95, 14), Z3 = (10, 14.95, 16.3). (14)
С использованием системы F-Ranking (см. http://www.swsys.ru/uploaded/image/2018-3/2018-3-dop/29.jpg) результаты ранжирования указанных нечетких чисел по всем методам, представленным в системе, приведены в таблице 1.
По результатам, представленным в таблице 1, можно видеть, что интегральное отношение предпочтения не является транзитивным.
В таблице 2 приведено ранжирование рассмотренных выше нечетких чисел с указанием соответствующего методу дефаззификации (Centroid Index, Median, Y2) значения; для методов FRAAI и FRAAY указана максимальная мера принадлежности данному рангу. Можно видеть, что для методов центра тяжести и медианы порядок рангов совпадает, а метод Y2 (метод интеграла средних значений a-срезов) имеет такой же порядок рангов, как и методы попарного сравнения. Кроме того, ранжирование указанных нечетких чисел по методам FRAAI и FRAAY совпадает для чисел из множеств S1 и S2 и отличается для множества S3. При этом показано также, что FRAAI – ранжирование, основанное на нетранзитивном отношении предпочтения RI, обладает свойством множественности рангов.
Необходимо отметить, что модели нетранзитивных отношений, имеющих место в реальном мире, привлекают внимание исследователей [14, 15]. Нечеткое отношение предпочтения RI, являющееся одним из наиболее интуитивно понятных среди имеющихся отношений предпочтения, а также основанный на концепции нечеткой приемлемости метод ранжирования FRAAI являются одной из немногих моделей исследования иррациональных/нетранзитивных порядков. Отметим также, что обобщенный метод ранжирования FRAAI является транзитивным [12].
Пример 2. Рассмотрим множество нечетких чисел S4 (A, B – трапециевидные, C – треугольное) (рис. 5):

S4: A = (1, 2, 5, 7), B = (2, 3, 5, 5.2),
C = (5, 6, 7). (15)
С помощью системы F-Ranking было проведено ранжирование нечетких чисел A, B из множества S4 (15) по методу центра тяжести, в результате были получены значения CI(A) = 3.778, CI(B) = 3.785 соответственно. Из этого следует:
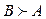 . (16)
. (16)
Рассмотрим множество S5 (рис. 6) трапециевидных нечетких чисел, полученных в результате сложения чисел из множества S4 (15):

S5: A + C = (6, 8, 11, 14),
B + C = (7, 9, 11, 12.2). (17)
По методу центра тяжести нечеткие числа A + C, B + C из множества S5 (17) имеют значения 9.788 и 9.77 соответственно. Из этого следует:
 . (18)
. (18)
Таким образом, из (16) и (18) следует, что для метода центра тяжести  [3].
[3].
Пример 3. Рассмотрим множество кусочно-линейных нечетких чисел S6 (рис. 7):


 (19)
(19)

По методу центра тяжести нечеткие числа A и B из множества S6 (19) имеют значения CI(A)=4.258, CI(B)=3.75 соответственно. Из этого следует
 . (20)
. (20)
Рассмотрим множество S7 (рис. 8) кусочно-линейных нечетких чисел A + C, B + C:

 (21)
(21)
По методу центра тяжести нечеткие числа A+C, B+C из множества S7 (21) имеют значения 7.022, 7.58 соответственно. Из этого следует
 (22)
(22)
Таким образом, из (20) и (22) следует, что для метода центра тяжести и заданных нечетких чисел A, B, C с кусочно-линейной функцией принадлежности  [3].
[3].
Пример 4. Рассмотрим множество треугольных нечетких чисел S8 (рис. 9):

S8: Z1 = (0, 2.3, 4), Z2 = (0.2, 1.55, 4.5),
W = (0.043, 0.1735, 0.304). (23)
По методу центра тяжести нечеткие числа Z1 и Z2 из множества S8 (23) имеют значения 2.1 и 2.083 соответственно. Из этого следует
 . (24)
. (24)
В отличие от двух предыдущих примеров, исследующих сложения исходных множеств, рассмотрим множество чисел S9 (рис. 10), получен- ных в результате перемножения чисел из множества S8 (23):
S9: Z1 ´ W, Z2 ´ W. (25)
По методу центра тяжести нечеткие числа Z1 ´ W и Z2 ´ W из множества S9 (25) имеют значения 0.494 и 0.506 соответственно. Из этого следует
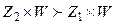 . (26)
. (26)
Таким образом (так же, как и в случае сложения в примерах 2, 3), из (24) и (26) следует, что для метода центра тяжести (и положительного нечеткого числа W) 
Пример 5. Рассмотрим множество треугольных нечетких чисел S10 (рис. 11):
S10: Z1 = (1, 1.2, 8.2), Z2 = (1, 4, 4.5),
W = (0.043, 0.1735, 1.3). (27)
По аналогии с предыдущим примером перемножим числа из (27), в результате получим нечеткие числа множества S11 (рис. 12):


S11: Z1 ´ W, Z2 ´ W. (28)
Ранжирование методом Юаня чисел из множеств S10 (27) и S11 (28) приводит к следующим результатам: m(Z2, Z1) = 0.577, m(Z1 ´ W, Z2 ´ W) = = 0.556. Из этого следует, что для метода Юаня 
Анализируя данный пример, можно отметить, что порядок ранжирования нарушается не только для метода центра тяжести, но и для других методов ранжирования.
В примере 5 вычисления производятся с десятью альфа-срезами. Для проверки корректности работы приложения F-Ranking нечеткие числа из множества S10 (27) были перемножены с разбиением на 20 альфа-срезов. После ранжирования были получены следующие результаты (для наглядности значения приведены с 7 знаками после десятичной точки): 10 альфа-срезов: m(Z2, Z1) = = 0.5774372, m(Z1 ´ W, Z2 ´ W) = 0.5557413, 20 альфа-срезов: m(Z2, Z1) = 0.5774372, m(Z1 ´ W, Z2 ´ W) = 0.5550221. Для сравнения: при 30 альфа-срезах m(Z1×W, Z2×W) = 0.5549033, то есть различие с аналогичным значением для 20 альфа-срезов составляет около 10-4.
Таким образом, можно говорить о корректности работы приложения F-Ranking; при этом количество альфа-срезов можно варьировать в зависимости от требований к точности выходных результатов.
Заключение
Система F-Ranking предоставляет широкие возможности для сравнения и ранжирования нечетких чисел. Она является особенно востребованной в случаях, когда визуальное/интуитивное ранжирование нечетких чисел невозможно (пример 1). Кроме того, система эффективна для проведения научных исследований (примеры 2–5). Наличие в программе сразу нескольких методов ранжирования: центра тяжести, медианы, интеграла средних значений α-срезов, а также метода Юаня и интегрального метода, в том числе дополнительных инструментов анализа при использовании двух последних методов, позволяет получить более полное представление о ранжируемых числах. Указанные характеристики делают систему F-Ranking удобным инструментом при решении широкого спектра научно-прикладных задач с использованием нечетких чисел. Программа спроектирована с учетом возможности добавления в нее других методов ранжирования. Разработанные программные библиотеки для ранжирования нечетких чисел используются в методах нечеткого многокритериального анализа решений для ранжирования альтернатив в условиях неопределенности.
Литература
1. Hatagar S., Halase S. Three input–one output fuzzy logic control of washing machine. Intern. J. of Sc. Research Eng. & Technology (IJSRET), 2015, vol. 4, pp. 57–62.
2. Samuel E.K. Fuzzy logic and its practical use in mass transit systems. 2005. URL: http://skisko.blogspot.com/2005/06/fuzzy-logic-and-its-practical-use-in.html (дата обращения: 26.12.2017).
3. Wang X., Kerre E. E. Reasonable properties for the ordering of fuzzy quantities (I). Fuzzy Sets and Systems, 2001, vol. 118, no. 3, pp. 375–385.
4. Wang X., Kerre E.E. Reasonable properties for the ordering of fuzzy quantities (II). Fuzzy Sets and Systems, 2001, vol. 118, no. 3, pp. 387–405.
5. Lee K.H. First course on fuzzy theory and applications. Springer Science & Business Media, 2006, vol. 27, 341 p.
6. Matarazzo B., Munda G. New approaches for the compare- son of L–R fuzzy numbers: a theoretical and operational analysis. Fuzzy Sets and Systems, 2001, vol. 118, no. 3, pp. 407–418.
7. Hanss M. Applied Fuzzy Arithmetic An Introduction with Engineering Applications. Springer-Verlag Berlin Heidelberg, 2005, 261 p.
8. Yatsalo B., Korobov A., Martínez L. Fuzzy multi-criteria acceptability analysis: A new approach to multi-criteria decision analysis under fuzzy environment. Expert Systems With Applications, 2017, vol. 84, pp. 262–271.
9. Allahviranloo T., Saneifard R. Defuzzification method for ranking fuzzy numbers based on center of gravity. Iranian J. of Fuzzy Systems, 2012, vol. 9, no. 6, pp. 57–67.
10. Ротштейн А.П., Штовба С.Д. Влияние методов дефаззификации на скорость настройки нечеткой модели // Кибернетика и системный анализ. 2002. № 5. С. 169–176.
11. Saneifard R., Saneifard R. The median value of fuzzy numbers and its applications in decision making. J. of Fuzzy Set Valued Analysis, 2012, vol. 2012, pp. 1–9.
12. Yatsalo B., Martinez L. Fuzzy rank acceptability analysis: a confidence measure of ranking fuzzy numbers. Proc. IEEE Transactions on Fuzzy Systems, 2018. DOI: https://doi.org/10.1109/TFUZZ. 2018.2838063.
13. Kahraman C., Bozdağ C.E. Fuzzy investment analysis using capital budgeting and dynamic programming techniques. Computational Intelligence in Economics and Finance. Springer Berlin Heidelberg, 2004, pp. 93–128.
14. Klimenko A.Y. Intransitivity in theory and in the real world. Entropy, 2015, vol. 17, no. 6, pp. 4364–4412.
15. Fishburn P.C. Nontransitive preferences in decision theory. J. of Risk and Uncertainty, 1991, vol. 4, no. 2, pp. 113–134.
References
- Hatagar S., Halase S.V. Three input–one output fuzzy logic control of washing machine. Intern. J. of Scientific Research Engineering & Technology (IJSRET). 2015, vol. 4, pp. 57–62.
- Samuel E.K. Fuzzy Logic and its Practical use in Mass Transit Systems. 2005. Available at: http://skisko.blogspot.com/2005/06/fuzzy-logic-and-its-practical-use-in.html (accessed December 26, 2017).
- Wang X., Kerre E.E. Reasonable properties for the ordering of fuzzy quantities (I). Fuzzy Sets and Systems. 2001,
vol. 118, no. 3, pp. 375–385.
- Wang X., Kerre E.E. Reasonable properties for the ordering of fuzzy quantities (II). Fuzzy Sets and Systems. 2001,
vol. 118, no. 3, pp. 387–405.
- Lee K.H. First Course on Fuzzy Theory and Applications. Springer-Verlag Berlin Heidelberg Publ., 2006, vol. 27,
341 p.
- Matarazzo B., Munda G. New approaches for the comparison of L–R fuzzy numbers: a theoretical and operational analysis. Fuzzy Sets and Systems. 2001, no. 118, pp. 407–418.
- Hanss M. Applied Fuzzy Arithmetic: an Introduction with Engineering Applications. Springer-Verlag Berlin Heidelberg Publ., 2005, 261 p.
- Yatsalo B., Korobov A., Martínez L. Fuzzy multi-criteria acceptability analysis: A new approach to multi-criteria decision analysis under fuzzy environment. Expert Systems with Applications. 2017, no. 84, pp. 262–271.
- Allahviranloo T., Saneifard R. Defuzzification method for ranking fuzzy numbers based on center of gravity. Iranian J. of Fuzzy Systems. 2012, no. 9, pp. 57–67.
- Rotshteyn A.P., Shtovba S.D. The influence of defuzzification methods on fuzzy model tuning speed. Cybernetics and Systems Analysis. 2002, no. 1, pp. 169–176.
- Saneifard R., Saneifard R. The median value of fuzzy numbers and its applications in decision making. J. of Fuzzy Set Valued Analysis. 2012, vol. 2012, pp. 1–9.
- Yatsalo B., Martinez L. Fuzzy rank acceptability analysis: A confidence measure of ranking fuzzy numbers. IEEE Trans. on Fuzzy Systems. 2018.
- Kahraman C., Bozdağ C.E. Fuzzy investment analysis using capital budgeting and dynamic programming techniques. Computational Intelligence in Economics and Finance. Springer Berlin Heidelberg Publ., 2004, pp. 93–128.
- Klimenko A.Y. Intransitivity in theory and in the real world. Entropy. 2015, no. 17, pp. 4364–4412.
- Fishburn P.C. Nontransitive preferences in decision theory. J. of Risk and Uncertainty. 1991, no. 4, pp. 113–134.
 , с непрерывной или кусочно-непрерывной сверху функцией принадлежности mz(x) Î [0, 1] (см. [5, 7]).
, с непрерывной или кусочно-непрерывной сверху функцией принадлежности mz(x) Î [0, 1] (см. [5, 7]). представляет множество нечетких чисел согласно определению 1.
представляет множество нечетких чисел согласно определению 1. (см. [5, 7]).
(см. [5, 7]). ´
´ , если mR(Zi, Zj) ³ 0.5;
, если mR(Zi, Zj) ³ 0.5; , если mR(Zi, Zj) > 0.5; (3)
, если mR(Zi, Zj) > 0.5; (3) , (4)
, (4) (площадь под кривой функции принадлежности) [3, 10].
(площадь под кривой функции принадлежности) [3, 10]. . (5)
. (5)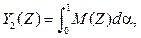 (6)
(6) под положительной частью (x ³ 0) данной функции принадлежности:
под положительной частью (x ³ 0) данной функции принадлежности: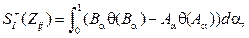 (7)
(7) (8)
(8) интерпретируется в этом случае как расстояние от положительной части нечеткого числа Zij = Zi – Zj = {[Aa, Ba]} до оси OY и вычисляется по формуле
интерпретируется в этом случае как расстояние от положительной части нечеткого числа Zij = Zi – Zj = {[Aa, Ba]} до оси OY и вычисляется по формуле , (9)
, (9) . (10)
. (10)




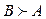 . (16)
. (16)
 . (18)
. (18) [3].
[3].

 (19)
(19)
 . (20)
. (20)
 (21)
(21) (22)
(22)
 . (24)
. (24)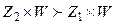 . (26)
. (26)



