Journal influence
Higher Attestation Commission (VAK) - К1 quartile
Russian Science Citation Index (RSCI)
Bookmark
Next issue
№4
Publication date:
09 December 2024
A program for calculation of controller settings by the method of advanced frequency characteristics
Date of submission article: 07.02.2018
UDC: 681.326
The article was published in issue no. № 3, 2018 [ pp. 636-639 ]Abstract:The paper considers the problem of calculating settings of typical general industrial controllers in automatic control systems for technological objects. It shows the possibility of applying the Nyquist stability criterion for extended system frequency characteristics. It also formulates the problem of ensuring the necessary quality of a transient process in a closed system due to the provision of the given degree of oscillation. The obtained condition for the given system oscillation ensures that the controller settings are located on the equal damping line. The paper considers the extended frequency characteristic of the PID controller for the case when a component is introduced into it as a real differentiating element. The authors have obtained the formulas for finding PID controller settings using extended frequency characteristics in the form of parametric dependencies. There are also relations obtained from general formulas for PI and PD controllers. A program developed in MatLab based on the proposed method allows calculating optimal controller settings by the criterion of minimum deviation of transient time and overshoot from the set values. There are also the results of calculating PID controller settings for a control example and the obtained equal damping lines. The paper presents the best transient processes for each of the equal damping lines and the optimal process satisfying the required quality characteristics. It also shows the disadvantages of the method of extended frequency characteristics in the proposed formulation. The paper considered the possibilities of alternative formulation of the problem of synthesizing controller settings and the application of the proposed methods for finding controller settings in multi-loop systems for automatic control of technological objects.
Аннотация:В статье рассмотрена постановка задачи расчета настроек типовых общепромышленных регуляторов в системах автоматического управления технологическими объектами. Показана возможность применения критерия устойчивости Найквиста для расширенных частотных характеристик систем. Сформулирована задача обеспечения необходимого качества переходного процесса в замкнутой системе за счет обеспечения заданной степени колебательности. Получено условие заданной колебательности системы, обеспечивающее нахождение настроек регулятора на линии равного затухания. Рассмотрена расширенная частотная характеристика ПИД-регулятора для случая введения в нее составляющей в виде реального дифференцирующего звена. Получены формулы для нахождения настроек ПИД-регулятора с использованием расширенных частотных характеристик в виде параметрических зависимостей. Приведены соотношения, получающиеся из общих формул для ПИ- и ПД-регуляторов. На основе предложенного метода в среде MatLab разработана программа, позволяющая рассчитать оптимальные настройки регулятора по критерию минимального отклонения времени переходного процесса и перерегулирования от заданных значений. Приведены результаты расчета настроек ПИД-регулятора для контрольного примера и полученные линии равного затухания. Показаны наилучшие по критерию качества переходные процессы для каждой из линий равного затухания и оптимальный процесс, удовлетворяющий требуемым характеристикам качества. Показаны недостатки метода расширенных частотных характеристик в предложенной постановке. Рассмотрены возможности альтернативной постановки задачи синтеза настроек регуляторов и применение предложенных методов для нахождения настроек регуляторов в многоконтурных системах автоматического управления технологическими объектами.
| Authors: Margolis B.I. (borismargolis@yandex.ru) - Tver State Technical University, Tver, Russia, Ph.D, G.A. Mansour (gubran_ali@mail.ru) - Tver State Technical University, Tver, Russia | |
| Keywords: the system of automatic control, overshoot, optimal settings, calculation program, equal damping line, oscillation degree, transient response, extended frequency response, calculation of settings, controller, subject, quality criteria |
|
| Page views: 10098 |
PDF version article Full issue in PDF (29.03Mb) |
| Permanent link: http://swsys.ru/index.php?id=4511&lang=en&page=article |
Print version Full issue in PDF (29.03Mb) |
| The article was published in issue no. № 3, 2018 [ pp. 636-639 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Структурная схема нечеткого регулятора на основе лингвистических переменных с четкими термами
- Построение структуры предметной области на основе анализа концептуальной схемы
- Использование энтропийных мер в задачах оценки информативности признаков распознавания образов
- Некоторые технологические аспекты создания учебно-тренировочных средств подготовки командиров и специалистов Военно-морского флота
- Разработка программного обеспечения для системы автоматического управления по выравниванию полуфабрикатов
Back to the list of articles
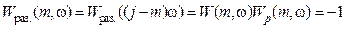 ,
, (3)
(3) (4)
(4) (5)
(5) (6)
(6)
 (7)
(7)
