Бурное развитие телекоммуникационных технологий, в частности, спутникового сегмента связи, предполагает использование как наземных, так и бортовых оконечных устройств с повышенными техническими характеристиками, к которым можно отнести массогабаритные, электродинамические показатели в целом, расширение зоны обслуживания спутниковым сегментом и т.д. Для реализации данной концепции предполагается использовать высокоэффективные антенные комплексы с современными системами управления, базирующиеся на основе нечеткой логики.
Для решения данной задачи будем использовать так называемые гибридные зеркальные антенны (ГЗА), так как данный вид антенн позволяет сформировать узкую многолучевую диаграмму направленности (ДН) с высоким коэффициентом усиления.
 ГЗА представляет собой антенную систему, состоящую из многоэлементной облучающей решетки и зеркала (рис. 1).
ГЗА представляет собой антенную систему, состоящую из многоэлементной облучающей решетки и зеркала (рис. 1).
Зеркало обычно выполнено в виде параболоида вращения. Облучающая решетка антенны состоит из набора активных облучателей определенной конструкции. Сама антенна имеет небольшую массу, простую конструкцию и низкую стоимость.
Согласно теории антенных систем, расчет ДН гибридной антенны можно провести по общей формуле для прямолинейной дискретной эквидистантной синфазной антенной решетки (АР) с известным амплитудным распределением. При этом вид и параметры ДН определяются размерами зеркала и видом амплитудного распределения в нем [1–4]. Нормированная ДН зеркальной антенны определяется на основании теоремы перемножения ДН:
F(q) = F0(q)Fc(q), (1)
где F0(q) – ДН одиночного элемента Гюйгенса,
 , (2)
, (2)
где Fc(q) – множитель АР.
Множитель системы должен рассчитываться по общему выражению с учетом амплитуды поля в каждой расчетной точке и ее координаты. Данное выражение известно из теории АР [5, 6] и имеет вид
 , (3)
, (3)
где En – амплитуда поля; Ф – угол раскрыва между фокальной осью и главным лепестком, град.; xn – реальная координата по раскрыву n-й расчетной точки, которую можно определить по формуле
 . (4)
. (4)
Подбирая в выражении (4) расстояние между соседними расчетными точками d, необходимо добиться, чтобы первая расчетная точка (n = 0) находилась на левом краю зеркала (при этом ее реальная координата по раскрыву  = R0), а последняя расчетная точка (N = 2Ф0) на правом краю зеркала (при этом ее реальная координата по раскрыву
= R0), а последняя расчетная точка (N = 2Ф0) на правом краю зеркала (при этом ее реальная координата по раскрыву  ). Рассчитав множитель системы, необходимо произвести нормировку результата и вычислить ДН антенны с помощью теоремы перемножения ДН. После расчета ДН строится ее график, по которому определяются параметры ДН (ширина и уровень боковых лепестков) [4, 7–14].
). Рассчитав множитель системы, необходимо произвести нормировку результата и вычислить ДН антенны с помощью теоремы перемножения ДН. После расчета ДН строится ее график, по которому определяются параметры ДН (ширина и уровень боковых лепестков) [4, 7–14].
В основе разрабатываемой системы управления такой антенны часто используется адаптивный алгоритм настройки ДН на пользователя. Реализация данного алгоритма порой вызывает некоторые трудности, связанные с тем, что весовые коэффициенты, настроенные по данному алгоритму, на практике не всегда способны реализовать необходимую ДН. Эти проблемы обусловлены несовершенством систем управления, построенных на традиционных электронных и программных модулях, случайными и преднамеренными электромагнитными помехами, а также меняющимися природными условиями (дождь, снег и т.д.) [9–14].
Для оперативного управления в реальном масштабе времени ДН подобной ГЗА необходимо применение высокоэффективных быстродействующих алгоритмов.
Традиционный алгоритм можно заменить алгоритмом управления АР на базе нечеткой логики. Он будет управлять амплитудно-фазовым распределением АР, что позволит формировать однолучевые и многолучевые ДН в зависимости от сложившейся ситуации.
Объектом управления будет офсетная ГЗА со сверхширокополосным планарно-щелевым облучателем (1 этаж, 6 рядов). В качестве оптического устройства (рефлектора) используется зеркало, а облучателя – фазированная АР [10–13].
В зависимости от сложившейся ситуации нечеткий регулятор на начальном этапе определяет рабочий сектор и значения амплитуды и фазы каждого излучателя АР в составе ГЗА. Затем нечеткий регулятор формирует управляющее воздействие в виде амплитуды и фазы, то есть амплитудно-фазового распределения, и подает эти значения на приемопередатчик, где происходит соответствующий сдвиг по фазе и формируется амплитуда на одном из излучателей. Таким образом, формируется главный лепесток в пределах рабочего сектора, соответственно сориентированного на ту или иную орбитальную позицию.
Системы на основе нечеткой логики основаны на использовании нечетких множеств, позволяющих отнести степень принадлежности конкретных физических величин к определенным терм-понятиям [9, 13, 15].
Нечеткая логическая система производит однозначное преобразование вектора входных сигналов в вектор выходных сигналов. Для этого преобразования используется механизм нечеткого вывода, основанный на знаниях, заложенных экспертом (то есть человеком).
Чтобы учесть описанные особенности процесса формирования ДН и большинство дестабилизирующих факторов, в качестве входного параметра необходимо рассматривать не только координаты пришедшего сигнала, но и текущие значения фазы и амплитуды, а также значение коэффициента стоячей волны (КСВ). Эта информация будет использоваться при построении базы правил системы нечеткого вывода, позволяющей реализовать данную модель нечеткого управления.
Для создаваемой системы нечеткого вывода в качестве входных переменных будем рассматривать четыре нечеткие лингвистические переменные. Для каждой из лингвистических переменных формируются терм-множества в виде нечетких переменных:  (координаты пришедшего сигнала) «1-й рабочий сектор», «2-й рабочий сектор», «3-й рабочий сектор»;
(координаты пришедшего сигнала) «1-й рабочий сектор», «2-й рабочий сектор», «3-й рабочий сектор»;
 (фаза) «очень маленький сдвиг», «маленький сдвиг», «небольшой сдвиг», «немалый сдвиг», «большой сдвиг»;
(фаза) «очень маленький сдвиг», «маленький сдвиг», «небольшой сдвиг», «немалый сдвиг», «большой сдвиг»;  (КСВ) «малый», «средний», «большой»;
(КСВ) «малый», «средний», «большой»; 
 (амплитуда) «малая», «небольшая», «большая», «очень большая».
(амплитуда) «малая», «небольшая», «большая», «очень большая».
 На рисунке 2 представлена структура системы нечеткого вывода в графическом виде. Для упрощения схемы показан выход на один из приемопередатчиков.
На рисунке 2 представлена структура системы нечеткого вывода в графическом виде. Для упрощения схемы показан выход на один из приемопередатчиков.
Для каждой переменной определим функции принадлежности нечетких множеств и приведем их аналитические и графические виды.
Аналитические выражения функции принадлежности нечеткого множества  :
:
 (5)
(5)
 (6)
(6)
 (7)
(7)
Аналитические выражения функции принадлежности нечеткого множества 
 :
:
 (8)
(8)
 (9)
(9)
 (10)
(10)
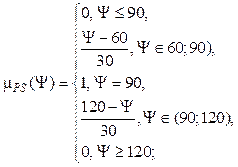 (11)
(11)
 (12)
(12)
Аналитические выражения функции принадлежности нечеткого множества  :
:
 (13)
(13)
 (14)
(14)
 (15)
(15)
Аналитические выражения функции принадлежности нечеткого множества  :
:
 (16)
(16)
 (17)
(17)
 (18)
(18)
 (19)
(19)
 Графический вид функций принадлежности нечетких множеств приведен на рисунке 3.
Графический вид функций принадлежности нечетких множеств приведен на рисунке 3.
Выходной лингвистической переменной является управляющее воздействие, представляющее собой функцию F(E, Ψ) нормированных значений от 1 до 10.
Основная характеристика всякой антенны – это функция, описывающая зависимость напряженности поля волны, излученной антенной, от углов. Определим поле волны в дальней зоне, то есть на достаточно большом расстоянии от антенны, там, где лучи, приходящие в некоторую произвольную точку пространства от любой точки антенны, можно считать параллельными [7].
Как правило, будем говорить о напряженности электрического поля Е, имея в виду, что в дальней зоне напряженность магнитного поля находится по простой формуле:
 , (20)
, (20)
где er – орт сферической системы координат; e0, m0 – магнитная и диэлектрическая проницаемость свободного пространства.
Напряженность поля характеризуется амплитудой, фазой и поляризацией. Можно записать:
 , (21)
, (21)
где k = 2p/l; r0 – расстояние от центра сферической системы координат до точки в дальней зоне.
Назовем, соответственно, Ф(q, a) амплитудной, Y(q, a) фазовой, e(q, a) поляризационной ДН. Последняя представляет собой единичный вектор, учитывающий направление вектора Е в дальней зоне.
Используем обозначение
 . (22)
. (22)
Векторную функцию Ф(q, a) называют комплексной векторной ДН. Она объединяет в себе амплитудную, фазовую и поляризационную ДН антенны. В большинстве случаев используем обозначение
 . (23)
. (23)
Назовем функцию (23) комплексной ДН и примем ее за нормированную функцию.
Функция реализована для каждого из приемопередатчиков, и получение нормированных значений как управляющих воздействий соответствует рабочему сектору.
Далее для выходной лингвистической переменной формируется терм-множество в виде нечетких переменных:  . Аналитические выражения функции принадлежности нечеткого множества
. Аналитические выражения функции принадлежности нечеткого множества  имеют следующий вид:
имеют следующий вид:
 (24)
(24)
 (25)
(25)
 (26)
(26)
 На рисунке 4 представлена функция принадлежности для термов выходной лингвистической переменной.
На рисунке 4 представлена функция принадлежности для термов выходной лингвистической переменной.
На основании входных и выходных лингвистических переменных формируется база продукционных правил системы нечеткого вывода.
Структурная схема нечеткого управления ГЗА представлена на рисунке (см. http://www.swsys.ru/ uploaded/image/2018-4/2018-4-dop/2.jpg). Основными данными являются показания с датчиков. Для управления потоками данных и хранения информации предназначены сервер БД и базы правил. Через трансивер управляющее воздействие от системы нечеткого управления поступает на сумматор сигнала. Далее сигнал поступает на диаграммообразующее устройство, которое формирует амплитудно-фазовое распределение поля в излучающей части в зависимости от сигнала, поступающего на соответствующий вход антенны.
Результаты работы нечеткого регулятора приведены на рисунке (см. http://www.swsys.ru/uploaded/image/2018-4/2018-4-dop/3.jpg).
Таким образом, применение нечеткого алгоритма в системе управления диаграммообразующим устройством позволит расширить зону покрытия спутникового ретранслятора, адаптировать процесс настройки земной станции спутникового приема, повысить пропускную способность канала связи, улучшить качество сигнала и помехозащищенность при различных условиях функционирования данных спутниковых терминалов.
Литература
1. Устройства СВЧ и антенны. Проектирование фазированных антенных решеток; [под ред. Д.И. Воскресенского]. М.: Радиотехника, 2012. 744 с.
2. Слюсар В.И. Цифровые антенные решетки в мобильной спутниковой связи // Первая миля. 2008. № 5. С. 16–21.
3. Белоусов О.А., Курносов Р.Ю., Горшков П.А., Рязано- ва А.Г. Антенная решетка на основе широкополосной планарно-щелевой антенны с экспоненциальным изменением ширины щели для систем беспроводного широкополосного доступа // Вопросы современной науки и практики. 2015. № 2. С. 184–194. DOI: 10.17277/voprosy.2015.02.рр.184-194.
4. Летунов А.А., Белоусов О.А., Колмыков Р.Ю., Колмыкова А.С., Курносов Р.Ю. Синтез гибридной зеркальной антенны для систем наземной спутниковой связи // Вопросы современной науки и практики. 2015. № 4. С. 107–113. DOI: 10. 17277/voprosy.2015.04.pp.107-113.
5. Белоусов О.А., Курносов Р.Ю., Горшков П.А., Рязано- ва А.Г. Синтез цилиндрической фазированной антенной решетки на основе логопериодических вибраторных антенн для систем широкополосного доступа стандарта IEE802.11, IEE802.16 // Вестн. ТГТУ. 2015. № 21. С. 266–272. DOI: 10.17277/vestnik.2015.02.pp.266-272.
6. Григорьев Л.Н. Цифровое формирование диаграммы направленности в фазированных антенных решетках. М.: Радиотехника, 2010. 144 с.
7. Вендик О.Г., Парнес М.Д., Бахрах Л.Д. Антенны с электрическим сканированием. Science Press. 2001. 252 с.
8. Алькубати А.Ф., Муромцев Д.Ю., Шамкин В.Н. Определение вероятностей состояний функционирования сложных систем при эрланговском распределении времен работы и восстановления их элементов // Вестн. Тамбовского гос. технич. уни-та. 2014. Т. 20. № 1. С. 6–16.
9. Dragone C. Unique reflector arrangement with very wide field of view for multibeam antennas. Electron. Lett, 1983, 19, no. 25, pp. 1061–1062.
10. Ohtomo I., Kumazawa H., Yamada Y., Minomo M. On-board K-band multibeam antennas configuration with low sidelobes and low crosspolarization. Electron. Lett, 1986, 22, no. 21, pp. 1121–1122.
11. Salmasi A.B., Rahmat-Samil Y. Beam area determination for multiple – beam satellite application. IEEE Trans. Aerospace and Electron. Syst. 1983, vol. 19, no. 3, pp. 405–412.
12. Stirland S.J., Fox G.P.D., and Malik D.P.S. Comparison between multifeed and shaped reflector satellite antennas for contoured beams. A92-29751 11-32, 1992, pt. 3, pp. 1571–1579.
13. Shogen K., Nishida H., Toyama N., Obuchi T., Miyata Y., Miyatani S. A study of a contoured beam antenna to future Japanese DBS. AIAA-92-2045-СР, 1992, pp. 1794–1802.
14. Dian D.D., Rahmat-Samit Y. A generalized diffraction synthesis technique for high performance reflector antennas. IEEE Trans., AP-43,1995, no. 1, рр. 27–40.
15. Леоненков А.В. Нечеткое моделирование в среде MATLAB и Fuzzy Tech. СПб: БХВ-Петербург, 2005. 736 с.
References
- Voskresensky D.I. Microwave Devices and Antennas. Designing of Phased Antenna Arrays. Moscow, Radiotekhnika Publ., 2012, 744 p.
- Slyusar V.I. Digital aerial arrays in mobile satellite communication. The First Mile. 2008, no. 5, pp. 16–21 (in Russ.).
- Belousov O.A., Kurnosov R.Yu., Gorshkov P.A., Ryazanova A.G. Antenna array for broadband planar slot antenna with an exponential change in the slot width for broadband wireless access systems. Problems of Contemporary Science and Practice. Vernadsky Univ. Tambov, 2015, no. 2, pp. 184–194 (in Russ.). DOI: 10.17277/voprosy.2015.02.рр.184-194.
- Letunov A.A., Belousov O.A., Kolmykov R.Yu., Kolmykova A.S., Kurnosov R.Yu. Synthesis of hybrid reflector antenna for terrestrial satellite communication system. Problems of Contemporary Science and Practice. Vernadsky Univ. Tambov, 2015, no. 4, pp. 107–113 (in Russ.). DOI: 10.17277/voprosy.2015.04.pp.107-113.
- Belousov O.A., Kurnosov R.Yu., Gorshkov P.A., Ryazanova A.G. Synthesis of cylindrical phased array based on log-periodic dipole antennas for broadband access standard IEE802.11, IEE802.16. Trans. of TSTU. Tambov, 2015, no. 21.
pp. 266–272 (in Russ.). DOI: 10.17277/vestnik.2015.02.pp.266-272.
- Grigorev L.N. Digital Beamforming in Phased Antenna Arrays. Moscow, Radiotekhnika Publ., 2010, 144 p.
- Vendik O.G., Parnes M.D., Bakhrakh L.D. Antennas with Electric Scanning. Science Press. 2001, 252 p.
- Alqubati A.F., Muromtsev D.Yu., Shamkin V.N. Defining the probabilities of functioning states of complicated systems under erlang distribution of work and restoration periods of its elements. Trans. of TSTU. Tambov, 2014, vol. 20, no. 1, pp. 6–16 (in Russ.).
- Dragone C. Unique reflector arrangement with very wide field of view for multibeam antennas. Electron. Lett. 1983, 19, no. 25, pp. 1061–1062.
- Ohtomo I., Kumazawa H., Yamada Y., Minomo M. On-board K-band multibeam antennas configuration with low sidelobes and low crosspolarization. Electron. Lett. 1986, 22, no. 21, pp. 1121–1122.
- Salmasi A.B., Rahmat-Samil Y. Beam area determination for multiple – beam satellite application. IEEE Trans. Aerospace and Electron. Syst. 1983, vol. 19, no. 3, pp. 405–412.
- Stirland S.J., Fox G.P.D., and Malik D.P.S. Comparison between multifeed and shaped reflector satellite antennas for contoured beams. A92-29751 11-32, 1992, pt. 3, pp. 1571–1579.
- Shogen K., Nishida H., Toyama N., Obuchi T., Miyata Y., Miyatani S. A study of a contoured beam antenna to future japanese DBS. AIAA-92-2045-СР, 1992, pp. 1794–1802.
- Dian D.D., Rahmat-Samit Y. A generalized diffraction synthesis technique for high performance reflector antennas. IEEE Trans., AP-43. 1995, no. 1, рр. 27–40.
- Leonenkov A.V. Fuzzy Modeling in MATLAB and Fuzzy Tech. St. Petersburg, BHV-Peterburg Publ., 2005, 736 p.




 , (2)
, (2) , (3)
, (3) . (4)
. (4) = R0), а последняя расчетная точка (N = 2Ф0) на правом краю зеркала (при этом ее реальная координата по раскрыву
= R0), а последняя расчетная точка (N = 2Ф0) на правом краю зеркала (при этом ее реальная координата по раскрыву  ). Рассчитав множитель системы, необходимо произвести нормировку результата и вычислить ДН антенны с помощью теоремы перемножения ДН. После расчета ДН строится ее график, по которому определяются параметры ДН (ширина и уровень боковых лепестков) [4, 7–14].
). Рассчитав множитель системы, необходимо произвести нормировку результата и вычислить ДН антенны с помощью теоремы перемножения ДН. После расчета ДН строится ее график, по которому определяются параметры ДН (ширина и уровень боковых лепестков) [4, 7–14]. (координаты пришедшего сигнала) «1-й рабочий сектор», «2-й рабочий сектор», «3-й рабочий сектор»;
(координаты пришедшего сигнала) «1-й рабочий сектор», «2-й рабочий сектор», «3-й рабочий сектор»;
 (фаза) «очень маленький сдвиг», «маленький сдвиг», «небольшой сдвиг», «немалый сдвиг», «большой сдвиг»;
(фаза) «очень маленький сдвиг», «маленький сдвиг», «небольшой сдвиг», «немалый сдвиг», «большой сдвиг»;  (КСВ) «малый», «средний», «большой»;
(КСВ) «малый», «средний», «большой»; 
 (амплитуда) «малая», «небольшая», «большая», «очень большая».
(амплитуда) «малая», «небольшая», «большая», «очень большая».
 :
: (5)
(5) (6)
(6) (7)
(7)
 :
: (8)
(8) (9)
(9) (10)
(10)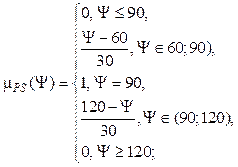 (11)
(11) (12)
(12) :
: (13)
(13) (14)
(14) (15)
(15) :
: (16)
(16) (17)
(17) (18)
(18) (19)
(19)
 , (20)
, (20) , (21)
, (21) . (22)
. (22) . (23)
. (23) . Аналитические выражения функции принадлежности нечеткого множества
. Аналитические выражения функции принадлежности нечеткого множества  имеют следующий вид:
имеют следующий вид: (24)
(24) (25)
(25) (26)
(26)
