В нелинейных элементах на высоких частотах начинают распространяться несколько типов электромагнитных волн. Это требует учета особенностей характеристик электромагнитных волн при решении различных задач нелинейной радиолокации (НРЛ). К числу таких устройств относятся решетки нелинейных щелевых излучателей (см. рисунок). В нелинейной решетке, состоящей из щелей, возникают новые особенности и связанные с ними технические возможности [1].
 Наиболее интересны такие щелевые решетки в НРЛ – информационной технологии, в основе которой лежит эффект рассеяния электромагнитных волн на объектах, обладающих нелинейными свойствами. Это направление исследований в технике представляет новую область радиолокации и вызывает большой интерес в научных кругах и у разработчиков программных и аппаратных систем получения информации об окружающей среде [2].
Наиболее интересны такие щелевые решетки в НРЛ – информационной технологии, в основе которой лежит эффект рассеяния электромагнитных волн на объектах, обладающих нелинейными свойствами. Это направление исследований в технике представляет новую область радиолокации и вызывает большой интерес в научных кругах и у разработчиков программных и аппаратных систем получения информации об окружающей среде [2].
Теоретическому расчету и конструктивному исследованию таких систем посвящен ряд работ, в которых предполагается использовать нестандартные аналитические методы электродинамического анализа, а именно решение интегральных и дифференциальных уравнений высокого порядка при помощи смены системы координат, решения гранич- ной задачи методом разделения переменной на основе разложения плоской электромагнитной волны в ряды по функции Матье, функций Бесселя и Ханкеля [3].
Наиболее современные разработки представлены в работах [4–6], в патентах и исследованиях [7, 8]. Использование способности некоторых объектов не только рассеивать падающие на них радиоволны, но и преобразовывать их спектр, позволяет рассматривать широкий круг задач, решение которых традиционными методами невозможно либо малопродуктивно.
При использовании таких нелинейных систем в многоволновом режиме из-за недоступности надежных средств расчета обычно не обходятся без трудоемкого эксперимента. На основании аналитических формул в ряде источников [9, 10] можно почерпнуть возможности разработки программ в интегрированных средах Visual Studio 2017 Profes- sional и RAD Studio на языке программирования C++ для численного расчета распределения дифрагированного поля в антенной системе с целью контроля характеристик.
Основной задачей является разработка программного инструмента, позволяющего моделировать дифракционную картину на плоском нелинейном (щелевом) датчике и таким образом учитывать особенности при их разработке и использовании.
Моделирование с помощью программного инструмента позволит провести строгий анализ работы нелинейных устройств и также оптимизировать их характеристики.
Электромагнитное поле, излучаемое таким нелинейным излучателем, представляет собой результат интерференции первичного поля и вторичного (дифрагированного), создаваемого системой токов, наведенных на поверхности первичным полем. Предполагается, что на нелинейный излучатель падает плоская, определенным образом поляризованная волна. Решение аналитической задачи сводится к системе парных интегральных уравнений относительно спектральных функций для плотностей поверхностных токов, решаемых методом моментов:
 (1)
(1)

Для численного моделирования с использованием разрабатываемого программного инструмента спектральных характеристик при дифракции электромагнитных волн воспользуемся методом моментов [1].
Суть метода заключается в следующем. Неизвестные функции  разлагаются в ряд по системе ортогональных на ширине излучателя функций:
разлагаются в ряд по системе ортогональных на ширине излучателя функций:
 (2)
(2)
Решение интегрального уравнения  x Î [c, d]; (с £ x £ d) ищем в виде суммы:
x Î [c, d]; (с £ x £ d) ищем в виде суммы:
 ,
, 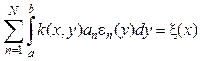 . (3)
. (3)
Для получения равенства проводим ортогонализацию по системе ортогональных функций. Для минимизации разности потребуем, чтобы уравнение (2) было ортогонально к каждому элементу весовых функций {hl} [9].
Правую часть уравнения (3) также представляем в виде суммы  на отрезке x Î [c, d], то есть проецируем обе части уравнения на сумму {hl}.
на отрезке x Î [c, d], то есть проецируем обе части уравнения на сумму {hl}.
В результате получаем систему уравнений:
 где 1 £ l £ L. (4)
где 1 £ l £ L. (4)
Таким образом, имеем систему уравнений с неизвестными коэффициентами ah:
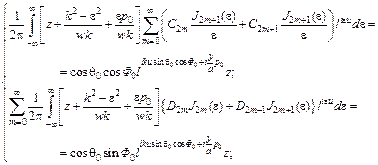

Умножаем на весовые функции и интегрируем.
Получаются следующие интегральные уравнения для спектральной плотности поверхностных токов:
 (5)
(5)


Рассмотрим эти интегралы:

 (6)
(6)
Выражение (6) – разложение по полной системе спектральных функций на ширине излучателя плотностей токов Jl(u), Jm(u).
В качестве таких функций берутся полиномы Якоби  на интервале u Î [–1; 1]. Они имеют весовые функции
на интервале u Î [–1; 1]. Они имеют весовые функции  , где
, где  . Для полиномов Чебышева 1-го рода – Tn(u); для полиномов Чебышева 2-го рода –
. Для полиномов Чебышева 1-го рода – Tn(u); для полиномов Чебышева 2-го рода –  , где
, где  :
:

при p = q = 0 – полиномы Лагранжа;
при  – полиномы Чебышева 1-го рода Tn(u);
– полиномы Чебышева 1-го рода Tn(u);
при  – полиномы Чебышева 2-го рода Tn(u).
– полиномы Чебышева 2-го рода Tn(u).
Данные функции должны удовлетворять теореме Винера–Пэли (функция f(t) = 0 при ½t½ ³ a, тогда ее преобразование Фурье 
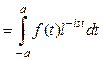 ).
).
Есть целая аналитическая функция экспоненциального типа £ a (r = 1; ¶ £ a или r < 1). Пусть y(s) – целая функция экспоненциального типа £ a, такая, что  (интеграл берется по действительной оси).
(интеграл берется по действительной оси).
Тогда существует функция f(t), равная 0 при ½t½ ³ a, преобразование Фурье которой равно y(s):
 , где
, где
 (7)
(7)
Полиномы Чебышева 2-го порядка ортогональны на интервале u Î [–1; 1] с весом p(k) =  , так что,
, так что,

Разложение спектральных функций Jl(u), Jm(u) по полиномам Um(u) имеет вид
 (8)
(8)
Для численного анализа спектральных функций по выражениям (8) в среде разработки RAD Studio написан программный имитатор. Он предназначен для моделирования спектральных характеристик в длинных и коротких волнах спектра. Для разработки выбран интерфейс с визуальными объектами, что предполагает использование событийного программирования и объектного подхода [10]. Для реализации событий выбран язык программирования Object Pascal.
Программный инструмент состоит из следующих частей.
1. Модуль bf – это главный модуль, в котором прописаны все остальные модули и подключаемые ресурсы.
2. Модуль bfwindow. Содержит описание главного окна, вкладок, главного и контекстного меню, а также сообщений пользователю, возникающих в процессе работы.
3. Модуль bfgraph. Содержит процедуры и функции для вывода графиков, их масштабирования, подписей по осям. Для работы с графикой в этом модуле подключается библиотека OpenGL. Также в этом модуле описана функция для работы с растровыми шрифтами (Lucida Console).
4. Модуль bfmethod. Содержит описание метода для подсчета первого приближения одиночного пика, для подсчета первого приближения (аппроксимация) одиночного пика и пары пиков в соответствии с методом наименьших квадратов. После этого в выделенной области рисуется график первого приближения. Все параметры тестируются, и в случае некорректности данных выдается соответствующая ошибка. Тестирование проводится как для одиночного пика, так и для пары пиков.
Экспериментальные данные о значениях переменных x и y задаются в таблице. Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью y = ax + b (найти параметры a и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные.
Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных a и b принимает наименьшее значение. То есть при данных a и b F(a, b) =  сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
5. Модуль bfderivator. Содержит набор функций, позволяющих взять частную производную, использующуюся в аппроксимации методом наименьших квадратов. В данном модуле в массив занесена таблица производных.
6. Модуль bfspecialfunc. Содержит специальную функцию для расчета параметра разрешенности пика, соответствующего определенной площади под пиком при конкретизированном значении амплитуды.
7. Модуль bfsysutils. Содержит функции преобразования типов и процедуру сортировки.
8. Модуль bftablefile. Предназначен для чтения файлов определенного типа (в данном случае файла, содержащего таблицу) с заранее задаваемым предполагаемым количеством колонок (в данном случае две колонки).
9. Модуль bfdialogs.
10. Модуль bfatd. Содержит абстрактные типы данных и множество операторов над ними для ком- пилятора и его связки с процедурой поиска наилучшего приближения.
11. Модуль bfcompiler. Является компилятором математических выражений любой сложности.
12. Модуль bfhjtechnique.
После запуска программного инструмента открывается окно, и далее необходимо загрузить файл со спектром. Спектр дифракции электромагнитной волны отобразится в виде графика на вкладке Дифракция (см. http://www.swsys.ru/upload ed/image/2018-4/2018-4-dop/18.jpg). Затем нужно задать область для анализа, которую можно увеличить.
Заданную область можно анализировать, например, посчитать первое приближение, которое будет построено в виде графика (см. http://www. swsys.ru/uploaded/image/2018-4/2018-4-dop/13.jpg). Полученные данные отображаются на вкладке Метод анализа (см. http://www.swsys.ru/uploaded/image/2018-4/2018-4-dop/12.jpg).
Разработанный программный инструмент может быть использован для анализа эффектов дифракции в нелинейном излучателе при проектировании в задачах радиолокации [1, 2, 10].
Основной результат исследования можно сформулировать как разработку программных методов анализа решеток нелинейных излучателей в многоволновом режиме приема, а также программной методики расчета дифракционных характеристик на частотах, превышающих основную частоту, с учетом неоднородности электромагнитных полей в данных условиях.
В рамках главного направления исследования решены следующие частные задачи:
- разработана математическая модель дифракции электромагнитной волны на нелинейном излучателе;
- в результате анализа получены формулы для расчета дифракционных зависимостей, которые дают удовлетворительное совпадение с экспериментальными данными;
- разработан программный имитатор для исследования эффектов дифракции электромагнитной волны.
Описываемое в данной работе ПО относится к подсистеме вторичной обработки [2]. Первичной называется обработка полученных результатов во время экспериментальных исследований в лаборатории научно-исследовательского центра прикладной электродинамики Казанского национального исследовательского технического университета имени А.Н. Туполева.
Литература
1. Пичугин В.Н., Пряников В.С., Седельников Ю.Е. Антенная решетка щелевых излучателей в многоволновом режиме приема: монография. Чебоксары: Изд-во Чуваш. ун-та, 2013. 116 с.
2. Пичугин В.Н., Бугрова И.Г. Исследование дифракции электромагнитных волн на нелинейных рассеивателях. Вып. 1. М.: Образование. Наука. Научные кадры, 2013. 134 с.
3. Semyonov E., Loschilov A. Measurements of the nonlinearity of the ultra wideband signals transformation. Ultra Wideband Communications: Novel Trends – System, Architecture and Implementation. Rijeka, Croatia, InTech, 2011, pp. 3–16. DOI: 10.5772/16867.
4. Иммореев И.Я. Сверхширокополосные радары. Особенности и возможности // Радиотехника и электроника. 2009. Т. 54. C. 5–31.
5. The Whirlwind. URL: http://vikhr.ru/product,137 (дата обращения: 13.03.2018).
6. Лощилов А.Г., Семенов Э.В., Малютин Н.Д., Мисю- нас А.О., Ильин А.А. Разработка устройств обработки сверх- широкополосных импульсных сигналов для исследования нелинейных свойств объектов методом нелинейной рефлек- тометрии // Докл. Томского гос. ун-та систем управления и радиоэлектроники. 2010. № 2. Ч. 1. С. 166–170.
7. Лихачев В.П., Усов Н.А. Способ нелинейной радиолокации. Пат. 2382380РФ. МПКG01S13/00. 2008131114/09; заявл. 28.07.2008; опубл. 20.02.2010.
8. Лощилов А.Г., Бибиков Т.Х., Семенов Э.В., Малю- тин Н.Д. Экспериментальная установка для исследования характеристик нелинейности объектов при воздействии импульсами пикосекундной длительности // СВЧ-техника и телекоммуникационные технологии: тр. 22-й Междунар. Крым. конф. Севастополь. 2012. С. 815–816.
9. MGV Spice models. Aeroflex URL: http://www.aeroflex.com/ams/Metelics/pdfiles/MGV_spice_models.pdf (дата обращения: 13.03.2018).
10. Культин Н.Б. Основы программирования в Embarcadero Delphi. СПб: БХВ-Петербург, 2015. 232 с.
References
- Pichugin V.N., Pryanikov V.S., Sedelnikov Yu.E. Antenna Array of Slot-Hole Emitters in Multi-Wave Reception Mode. Monograph. Cheboksary, 2013, 116 p.
- Pichugin V.N., Bugrova I.G. The Study of Diffraction of Electromagnetic Waves on Nonlinear Scatterers. Iss. 1. Moscow, Obrazovanie. Nauka. Nauchnye kadry Publ., 2013, 134 p.
- Semyonov E., Loschilov A. Measurements of the nonlinearity is of the ultra wideband signals transformation. Ultra Wideband Communications: Novel Trends – System, Architecture and Implementation. Rijeka, Croatia, InTech Publ., 2011, pp. 3–16. DOI: 10.5772/16867.
- Immoreev I.Ya. Ultrawideband radars. Features and capabilities. J. of Communications Technology and Electronics. 2009, vol. 54, no. 1, pp. 5–31.
- The Whirlwind. Available at: http://vikhr.ru/product 137 (accessed March 13, 2018).
- Loshchilov A.G., Semenov E.V., Malyutin N.D., Misyunas A.O., Ilyin A.A. Development of devices of processing of UWB pulse signals to study the nonlinear properties of objects by the method of nonlinear reflectometry. Proc. of TUSUR Univ. 2010, no. 2, part 1, pp. 166–170 (in Russ.).
- Likhachev V.P., Usov N.A. Nonlinear Radar Method. Patent RF no. 2382380. IPCG01S13/00. 2010.
- Loshchilov A.G., Bibikov T.Kh., Semenov E.V., Malyutin N.D. Experimental setup to study the characteristics of nonlinearity objects when exposed to pulses of picosecond duration. Proc. 22th Intern. Crimea Conf. “Microwave and Telecommunication Technologies” (Computer Vision'2012). Sevastopol, 2012, pp. 815–816 (in Russ.).
- MGV Spice Models. Aeroflex. Available at: http://www.aeroflex.com/ams/Metelics/pdfiles/MGV_spice_models.pdf (accessed March 13, 2018).
- Kultin N.B. Programming Bases in Delphi Embarcadero. St. Petersburg, BHV-Peterburg Publ., 2015, 232 p.

 (1)
(1)
 разлагаются в ряд по системе ортогональных на ширине излучателя функций:
разлагаются в ряд по системе ортогональных на ширине излучателя функций: (2)
(2) x Î [c, d]; (с £ x £ d) ищем в виде суммы:
x Î [c, d]; (с £ x £ d) ищем в виде суммы: ,
, 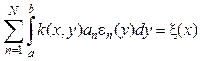 . (3)
. (3) на отрезке x Î [c, d], то есть проецируем обе части уравнения на сумму {hl}.
на отрезке x Î [c, d], то есть проецируем обе части уравнения на сумму {hl}. где 1 £ l £ L. (4)
где 1 £ l £ L. (4)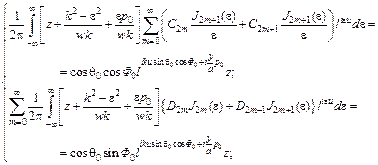

 (5)
(5)


 (6)
(6) на интервале u Î [–1; 1]. Они имеют весовые функции
на интервале u Î [–1; 1]. Они имеют весовые функции  , где
, где  . Для полиномов Чебышева 1-го рода – Tn(u); для полиномов Чебышева 2-го рода –
. Для полиномов Чебышева 1-го рода – Tn(u); для полиномов Чебышева 2-го рода – 
 – полиномы Чебышева 1-го рода Tn(u);
– полиномы Чебышева 1-го рода Tn(u); – полиномы Чебышева 2-го рода Tn(u).
– полиномы Чебышева 2-го рода Tn(u).
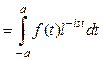 ).
). (интеграл берется по действительной оси).
(интеграл берется по действительной оси). , где
, где (7)
(7) , так что,
, так что,
 (8)
(8) сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.