Software & Systems

Постоянно растущий объем данных требует создания алгоритмов для их обработки. По этой причине в ряде областей задачи машинного обучения и интеллектуального анализа данных становятся все более распространенными и актуальными. Важное место в них занимает извлечение признаков, поскольку использование слабо релевантных признаков резко снижает эффективность любых алгоритмов. И если еще 10–20 лет назад был распространен ручной подбор признаков [1], то сейчас наиболее перспективными являются нейросетевые алгоритмы, осуществляющие автоматический подбор признаков в процессе решения задачи. Это позволяет сократить ручной объем работы для исследователей, а в ряде случаев и повысить качество работы [2]. Однако глубокие нейронные сети сложны с вычислительной точки зрения, что затрудняет их применение в высоконагруженных системах с жесткими требованиями по времени ответа.

Кроме того, глубокие нейронные сети плохо подходят для решения задач онлайнового (динамического) обучения, поскольку они статичны и не могут обучаться в режиме реального времени.  По этой причине в подобных задачах легкие модели (например, логистическая регрессия) зачастую выигрывают у тяжеловесных, поскольку позволяют обновлять параметры в режиме реального времени. Однако столь простые модели требуют ручного подбора признаков, что отнимает много времени у исследователей, и порой необходимо привлечение к работе экспертов заданной предметной области. В работе [3] авторами была предложена нейронная сеть, которая осуществляет ав- томатизированный подбор признаков, поддерживая при этом обновление параметров в режиме реального времени. Данная статья посвящена вопросам программной реализации этой архитектуры.

Описание архитектуры

Рассматриваемая модель представляет собой нейронную сеть с одним скрытым слоем. Отличие от традиционного персептрона заключается в разреженности архитектуры: нейроны скрытого слоя связаны только с частью нейронов входного слоя. Выходной слой нейронной сети состоит из одного нейрона с сигмоидальной функцией активации, которая выдает вероятность для заданного набора входных параметров.

На вход модель принимает заданное количество признаков. Сами признаки категориальные, и для их подачи на вход применяется унитарное кодирование [4]. Каждому признаку отводится одинаковый диапазон значений во входном векторе. Схема архитектуры представлена на рисунке 1.

Специфичность данной архитектуры заключается в том, что она имеет разреженные связи с определенной структурой. И это дает ей ряд преимуществ.

Особенности разреженной нейросетевой архитектуры

Исследования работы головного мозга показывают, что биологические нейроны кодируют информацию в разреженном и распределенном видах. Согласно оценкам, процент активных нейронов в один и тот же момент времени колеблется от 1 до 4. Это соответствует балансу между разнообразием возможных представлений и небольшим потреблением энергии. Традиционные сети прямого распространения без использования L1 регуляризации не обладают таким свойством. Например, при использовании сигмоидальной функции активации нейроны после начальной инициализации имеют устойчивое состояние на середине между режимами насыщения. Это выглядит неестественно с биологической точки зрения и вредит оптимизации на основе градиентного спуска.

Разреженные представления имеют несколько преимуществ [5]. В контексте рассматриваемой задачи стоит выделить эффективное представление данных переменного размера. Различные входы могут содержать разное количество информации, и потому их более удобно представлять в виде структур с переменным размером. Стоит отметить, что слиш- ком высокая степень разреженности может приводить к деградации модели, поскольку она сокращает ее емкость. Однако на сегодняшний день известно, что глубокие нейронные сети часто содержат избыточное число параметров (что приводит к усложнению вычислений и росту потребления ресурсов), поэтому их можно значительно упростить без существенной потери качества [6]. Помимо вычислительной избыточности, большое количество параметров зачастую ухудшают обобщающую способность моделей, делая их более подверженными переобучению.

Следовательно, можно удалить много параметров нейронной сети без существенного ухудшения (а порой и с улучшением) производительности. Разумеется, такие изменения приводят к возникновению разреженных архитектур. Помимо пониженных требований к памяти (нужно хранить меньшее число параметров), сокращение числа параметров позволяет упростить итоговые вычисления и уменьшить время предсказания, что играет роль в высоконагруженных системах или в системах, работающих со слабым аппаратным обеспечением.

Есть различные стратегии сокращения параметров нейронных сетей. Стратегии усечения весов были предложены еще Лекуном в работе [7], и они же остаются наиболее популярными до настоящего времени. Относительно недавно в работе [8] был предложен алгоритм сокращения количества связей, основанный на похожести нейронов. Стратегия прореживания нейронной сети может быть также встроена в обучение модели. Еще один подход заключается в обучении маленькой модели, которая по своему поведению будет имитировать большую модель [9]. Кроме того, в некоторых работах предлагается обучать глубокие модели, но с меньшим числом параметров. Оставшиеся параметры при этом должны предсказываться на основании уже обученных.

В предложенной нейросети разреженность уже заложена в саму архитектуру с учетом решаемой задачи (предсказание поведения пользователей в Интернете). Это осложняет ее реализацию на базе таких нейросетевых фреймворков, как Pytorch, Tensorflow, Theano и т.д. Разреженность связей можно реализовать при помощи обнуления некоторых весовых коэффициентов или путем использования модулей Sparse. Однако полученная реализация получается в несколько раз медленнее, чем простая логистическая регрессия, что осложняет переход на нее в высоконагруженных системах. По этой причине для применения данной архитек- туры в задаче предсказания поведения пользователей в Интернете было принято решение разработать самостоятельную программную реализацию, оптимизированную непосредственно под данную архитектуру. Далее рассматривается концепция программной реализации и описываются разработанные алгоритмы, позволяющие обеспечить быстродействие предложенной нейронной сети.

Диаграмма классов системы

Диаграмма основных классов реализованной библиотеки представлена на рисунке 2. Класс feature_t используется для описания поддерживаемых признаков в модели, level_t – для описания уровня модели, который может состоять из нескольких признаков (в таком случае применяется класс hashing trick [10]), а levels_holder_t описывает конфигурацию модели целиком (модель состоит из набора уровней). Помимо конфигурации, у модели есть набор настроек (к примеру, количество элементов, отводимых на представление каждого признака), который описывается классом lr_settings_t. В результате класс самой нейросетевой модели наследует от класса настроек и класс конфигурации модели. Сама нейросетевая модель описывается двумя классами: класс neural_net_t позволяет только использовать модель (загрузив ее предварительно из дампа), а класс neural_net_fitter_t – обучать. Такое разделение дает возможность программным компонентам, которые только используют обученную модель, не хранить множество дополнительных параметров, связанных с настройками обучения. Из рисунка 2 видно, что класс lr_settings_t оказывается включенным дважды. Для разрешения этой ситуации используется виртуальное наследование. Также с классом neural_net_fitter_t жестко связан объект оптимизатора (композиция), то есть он создается в конструкторе класса neural_net_fitter_t. Разделение оптимизаторов и самих моделей дает потенциальную возможность использовать одни и те же оптимизаторы для обучения разных моделей.

Структуры данных и алгоритмы создания нейросети

Для реализации выбран язык программирования C++, так как он включает в себя множество современных инструментов программирования, таких как лямбда-функции, move-семантика, умные указатели и т.д., сохраняя при этом хорошую производительность [11].

Архитектура нейросети задается статически и хранится в двумерном массиве. Входные данные поступают в виде набора из L признаков, каждый из которых имеет N различных значений. Таким образом, входное пространство значений разбито на L диапазонов, каждый из которых соответствует одному признаку. С учетом архитектуры сети количество нейронов скрытого слоя равняется 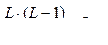. Поскольку сеть не является полносвязной, хранить полную матрицу весов (с нулевыми весами в позициях, где нет связей) расточительно, поэтому в разработанной реализации хранятся только ненулевые коэффициенты. Благодаря фиксированной архитектуре можно заранее рассчитать размер такой матрицы с ненулевыми коэффициентами. Чтобы по номеру набора признаков li быстро получать затронутые номера нейронов скрытого слоя, была создана матрица соединений нейронной сети. В этой матрице каждому номеру признака на входном слое соответствует список затронутых номеров нейронов скрытого слоя. Для нейронной сети, где L = 5 (5 различных категориальных признаков), данная матрица выглядит так, как показано в таблице 1.

Таблица 1

Пример матрицы соединений для пяти признаков

Table 1

The example of a matrix of coupling for 5 features

Для формирования такой матрицы сначала заполняется вспомогательный двумерный массив соединений для нейронов скрытого слоя (для каждого нейрона скрытого слоя содержится массив с номерами связанных с ним нейронов входного слоя). Количество строк равняется количеству нейронов скрытого слоя, а количество столбцов – числу связей каждого нейрона (для данной архитектуры оно равно 1 или 2). Для нейронной сети из пяти признаков такая вспомогательная структура имеет вид, представленный в таблице 2.

Таблица 2

Вспомогательная матрица для нейронной сети с пятью признаками

Table 2

A utility matrix for a neural network with 5 features

Такая структура данных заполняется на основе модульной арифметики. Приведем алгоритм ее заполнения (рис. 3).

Сложность такого алгоритма составляет O(n2), где n – количество уровней в модели. Учитывая, что n не превышает нескольких десятков, это не является проблемой. Кроме того, создание архитектуры нейросети делается только один раз за всю работу сети, поэтому доля затраченного на это времени крайне незначительна. Чтобы из такой вспомогательной матрицы получить основную матрицу связей, достаточно однократного прохода по циклу. Алгоритм 2 описывает формирование матрицы соединений нейронной сети (рис. 4).

Сложность данного алгоритма составляет O(n3), где n – количество уровней модели (поскольку количество скрытых нейронов сети пропорционально квадрату числа уровней в модели). Однако и это не является проблемой по тем же причинам, что и в алгоритме 1. В итоге для каждого значения входного признака можно получить номера связанных с ним нейронов скрытого слоя. Поскольку каждый нейрон входного слоя связан ровно с L нейронами скрытого слоя, веса нейронов скрытого слоя можно хранить в матрице размерности N×L×L. В случае полносвязной сети аналогичного размера для хранения весов скрытого слоя потребовалась бы матрица размера 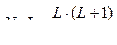, то есть в L/2 раз больше. При L = 20 признакам получается экономия памяти в 10 раз.

Порядок создания нейронной сети с учетом вспомогательных объектов изображен на диа- грамме последовательности (рис. 5), на которой видно, что при создании объекта нейросети сначала инициализируется объект настроек, затем создается конфигурация уровней, после чего инициализируются параметры обучения модели. Затем по вышеописанному алгоритму формируется нейронная сеть с заданной структурой, после чего создается объект оптимизатора. При создании объекта оптимизатора используются параметры обучения модели.

Последовательность обработки примера нейросетью

Обработка примеров нейронной сетью производится в следующей последовательности:

-     расчет номеров затронутых индексов (в силу разреженности данных для одного примера затрагиваются лишь несколько индексов);

-     получение номера уровня (это делается по номеру индекса, так как на каждый признак отводится одинаковое количество значений);

-     получение номеров нейронов скрытого слоя, с которыми связан данный уровень (с использованием матрицы, изображенной в таблице 1);

-     расчет взвешенной суммы для нейрона выходного слоя;

-     переиспользование рассчитанного набо­ра индексов для предсказания и обновления.

Процесс суммирования нейронов скрытого слоя изображен на рисунке 6. Основная особенность суммирования заключается в том, что оно производится не по нейронам скрытого слоя, а по весам. Сначала рассчитывается вклад во все нейроны скрытого слоя от первого признака, затем – от второго и т.д. Такой способ суммирования позволяет получить ускорение за счет локального расположения в памяти слагаемых (весов).

При предсказании сначала производится расчет затронутых индексов и значений нейронов скрытого слоя. Эти значения используются при получении предсказания. Во время обучения сначала предсказывается вероятность для данного примера, затем рассчитывается функция потерь, на основании которой вычисляются градиенты и обновляются коэффициенты. При этом переиспользуются индексы и значения коэффициентов на скрытом слое, полученные при обучении модели. Последнее позволяет значительно сократить время, затрачиваемое моделью на обработку одного примера.

Основные элементы процедуры обучения изображены на диаграмме активности (рис. 7). Отметим, что некоторые этапы расчета градиентов выполняются параллельно. После обучения модели на каждом примере производится расчет метрики кросс-энтропия. В данной метрике суммарная ошибка на выборке складывается из ошибок по отдельным примерам, поэтому ее удобно использовать в задачах онлайнового обучения для контроля качества работы модели. Если по какой-либо причине не удалось получить предсказание для данного примера, то и обучение также не производится.

Сравнение скорости обработки примеров с другими реализациями

После разработки вышеописанной архитектуры были проведены измерения для сравнения времени ее работы с реализациями, сделанными на базе уже имеющихся библиотек. В сравнениях участвовали четыре реализации.

1. Собственная реализация логистической регрессии с хешированием составных признаков [10]. Использовались 15 комбинаций признаков.

2.  Вышеописанная реализация нейронной сети с использованием простых признаков на входе.

3. Реализация предложенной архитектуры нейронной сети на базе библиотеки Lasagne с использованием разреженных матриц [12].

 4. Реализация предложенной архитектуры на базе Pytorch [13]. На момент проведения экспериментов была доступна версия pytorch 0.4.1 (дата релиза – июль 2018 года) без поддержки автоматического расчета градиентов для разреженных матриц. Поэтому реализация данной архитектуры была произведена на базе плотных матриц.

В эксперименте производились измерения для разной размерности, отводимой на каждый признак. Количество коэффициентов, отводимых на признак, изменялось от 28 до 216. Всего использовалось 15 признаков. Таким образом, общий размер входного вектора изменялся от 4 тысяч до 1 млн признаков. Замерялось время получения предсказаний для 100 тысяч примеров и обновления модели на 100 тысяч при- меров (1 итерация). Замеры производились на сервере с процессором Intel Xeon CPU E5-2667 3.30 GHz и оперативной памятью Micron 36KSF2G72PZ-1 1333 MHz (0.8ns) объемом 256 Гб.

Результаты измерений для предложенной архитектуры приведены на рисунках 8 и 9.

На графиках видно, что разработанная реализация нейронной сети работает практически так же, как логистическая регрессия, и на поря- док быстрее реализации на базе Lasagne. Реализация на базе Pytorch при увеличении размера вектора начинает работать значительно медленнее, поскольку она основана на плотных, а не на разреженных матрицах. Разработанная архитектура легко расширяема до поддержки не только пар, но и троек, четверок признаков и т.д. Однако в нейронной сети, в которой каждый нейрон скрытого слоя связан с тремя нейронами на входном слое, время предсказания и обучения значительно возрастает.

Заключение

В целом можно сделать вывод, что благодаря описанным оптимизациям разработанная реализация позволяет получить ускорение примерно в 10 раз по сравнению с реализацией, написанной на уже готовых нейросетевых фреймворках. Таким образом, использование разработанной реализации целесообразно на практике, особенно в высоконагруженных системах, работающих в режиме реального времени, и только в том случае, когда каждый нейрон скрытого слоя связан с небольшим количеством нейронов на входе. В противном случае предпочтительно использовать традиционные плотные матрицы.

Литература

1.    Guyon I., Gunn S., Nikravesh M., Zadeh L. Feature Extraction: Foundations and Applications. Studies in Fuzziкness and Soft Computing. Springer, 2008, 773 p.

2.    Бенджио И., Гудфеллоу Я., Курвилль А. Глубокое обучение; [пер. с англ. А. Слинкина]. М.: ДМК-Пресс, 2018. 652 с.

3.    Fedorenko Yu.S., Gapanyuk Yu.E. The neural network with automatic feature selection for solving problems with categorical variables. Proc. XX Int. Conf. Neuroinformatics. Springer, 2018, vol. 799, pp. 129–135.

4.    Харрис С.Л., Харрис Д.М. Цифровая схемотехника и архитектура компьютера; [пер. с англ.]. М.: ДМК-Пресс, 2018. 792 с.

5.    Glorot X., Bordes A., Bengio Y. Deep Sparse Rectifier Neural Networks. Proc. Intern. Conf. PMLR, 2011, pp. 315–323.

6.    Molchanov D., Ashukha A., Vetrov D. Variational dropout sparsifies deep neural networks. Proc. 34th Intern. Conf. PMLR, 2017, pp. 2498–2507.

7.    LeCun Y., Denker J., Solla S. Optimal brain damage. Proc. Conf. NIPS, 1989, vol. 2, pp. 598–605.

8.    Srinivas S., Venkatesh B. Data-free parameter pruning for Deep Neural Networks. 2015. URL: https://arxiv.org/abs/1507.06149 (дата обращения: 11.05.2019).

9.    Bucila С., Caruana R., Niculescu-Mizil A. Model compression. Proc. ACM SIGKDD Intern. Conf., USA, 2006, pp. 535–541. DOI: 10.1145/1150402.1150464.

10. ISOCPP: C++ 11 Overview. URL: https://isocpp.org/wiki/faq/cpp11 (дата обращения: 11.05.2019).

11. Weinberger K., Dasgupta A., Langford J., Smola A., Attenberg J. Feature hashing for large scale multitask learning. Proc. 26th ICML, Canada, 2009, pp. 1113–1120. DOI: 10.1145/1553374.1553516.

12. Lasagne: Docs, Welcome to Lasagne. URL: https://lasagne.readthedocs.io/en/latest/ (дата обращения: 11.05.2019).

13. Pytorch. Tensors and Dynamic neural networks in Python with strong GPU acceleration. URL: http://pytorch.org/ (дата обращения: 11.05.2019).

References

1. Guyon I., Gunn S., Nikravesh M., Zadeh L. Feature Extraction: Foundations and Applications. Studies in Fuzziness and Soft Computing. Springer, Berlin Heidelberg, 2008, 773 p.
2. Bengio Y., Goodfellow I., Courville A. Deep Learning. MIT Press, 2016, 800 p. (Russ. ed.: A. Slinkin, Moscow, DMK-Press, 2018, 652 p.).
3. Fedorenko Yu.S., Gapanyuk Yu.E. The Neural Network with Automatic Feature Selection for Solving Problems with Categorical Variables. Proc. XX Int. Conf. Neuroinformatics. Springer Publ., 2018, vol. 799, pp. 129–135.
4. Harris S.L., Harris D.M. Digital Design and Computer Architecture. 2nd ed., Moscow, DMK-Press, 2018, 792 p.
5. Glorot X., Bordes A., Bengio Y. Deep Sparse Rectifier Neural Networks. Proc. Intern. Conf. PMLR. 2011, pp. 315–323.
6. Molchanov D., Ashukha A., Vetrov D. Variational Dropout Sparsifies Deep Neural Networks. Proc. 34th Intern. Conf. on Machine Learning, PMLR. 2017, pp. 2498–2507.
7. LeCun Y., Denker J., Solla S. Optimal brain damage. Proc. Conf. NIPS, 1989, vol. 2, pp. 598–605.
8. Srinivas S., Venkatesh B. Data-Free Parameter Pruning for Deep Neural Networks. 2015. Available at: https://arxiv.org/abs/1507.06149 (accessed May 11, 2019).
9. Bucila С., Caruana R., Niculescu-Mizil A. Model compression. Proc. 12th ACM SIGKDD Intern. Conf. on Knowledge Discovery and Data Mining. USA, 2006, pp. 535–541. DOI: 10.1145/1150402.1150464.
10. ISOCPP: C++ 11 Overview. Available at: https://isocpp.org/wiki/faq/cpp11 (accessed May 11, 2019).
11. Weinberger K., Dasgupta A., Langford J., Smola A., Attenberg J. Feature hashing for large scale multitask learning. Proc. 26th Intern. Conf. on Machine Learning, ICML. Canada, 2009, pp. 1113–1120. DOI: 10.1145/1553374.1553516.
12. Lasagne: Docs, Welcome to Lasagne. Available at: https://lasagne.readthedocs.io/en/latest/ (accessed May 11, 2019).
13. Pytorch. Tensors and Dynamic Neural Networks in Python with Strong GPU Acceleration. Available at: http://pytorch.org/ (accessed May 11, 2019).