Software & Systems

По мнению военных экспертов, уровень развития информатики и вычислительной техники может стать одним из главных факторов достижения успеха в военных конфликтах будущего, определяя технический облик перспективного вооружения [1].

Данное обстоятельство обусловливает на­личие большого количества отечественных и зарубежных научно-исследовательских организаций, высших учебных заведений, а также коммерческих предприятий, активно занимающихся теорией и практикой в области информатики и вычислительной техники.

Анализ научно-технической литературы показывает, что одним из важнейших направле- ний в области информатики и вычислительной техники является создание и применение суперкомпьютеров [2–5]. Это направление во всем мире относится к факторам стратегического потенциала оборонного, научно-технического и народнохозяйственного назначения [1].

Создание и применение суперкомпьютеров в военной сфере обусловлены объективной потребностью в огромных вычислительных ресурсах для решения таких военно-прикладных задач, как

-     обеспечение проведения научной работы (обеспечение выполнения в установленном порядке научно-исследовательских и опытно-конструкторских работ);

-     информационная поддержка органов военного управления (мониторинг и прогнозирование состояния войск (сил), военно-политической и общественно-политической обстановки);

-     численное моделирование (моделирование поражающих факторов, сложных динамических объектов);

-     имитационное моделирование (моделирование обеспечения войск (сил), боевых действий);

-     виртуальное моделирование образцов вооружения, военной и специальной техники на основе технологий цифровых двойников и дополненной реальности;

-     обработка неструктурированной и слабоструктурированной информации на основе технологий больших данных.

Важнейшей аспектом при создании и применении суперкомпьютеров в военном деле является разработка архитектурных решений, обеспечивающих максимальную производительность на широком классе военно-прикладных задач [1]. Постоянное изменение качественного состава военно-прикладных задач, технологий производства вычислительных систем, алгоритмов обработки информации обусловливает требование к непрерывному совершенствованию научно-методического аппарата проектирования вычислительных систем специального назначения. Поэтому разработка качественно нового научно-методического аппарата обоснования архитектур суперкомпьютеров, основанного на принципах унификации, комплексирования и интеграции и обеспечивающего максимальную производительность, является одной из важнейших научных задач в военном деле.

Представление архитектуры суперкомпьютера с помощью модели коллектива вычислителей

Архитектура суперкомпьютера как любой другой вычислительной системы – совокупность средств и правил, обеспечивающих взаимодействие устройств обработки информации и программ [6–8].

Разработка архитектуры суперкомпьютера подразумевает решение следующих вопросов:

–     выбор типов применяемых элементов и определение технических характеристик каждого из них;

–     выбор методов управления и синхрони- зации системы;

–     выбор стратегии передачи информации между элементами суперкомпьютера;

–     выбор типа каналов связи;

–     деление на разделяемые и индивидуальные ресурсы;

–     адаптация суперкомпьютера к алгоритмам.

Каноническую основу архитектуры суперкомпьютера может составить модель коллектива вычислителей, которая представляется парой:

S = ,                                             (1)

где H и A – конструкция и алгоритм работы коллектива вычислителей [9].

Конструкция коллектива вычислителей описывается в виде

H = ,                                            (2)

где C = {ci} – множество вычислителей {ci}, i = 0(1)N–1; N – мощность множества C; G – описание структуры коллектива вычислителей (сети связей между вычислителями).

Конструкция коллектива вычислителей представляет отражение следующих основополагающих архитектурных принципов [9–11].

1. Параллелизм при обработке информации (параллельного вычисления операций на множестве C вычислителей, взаимодействующих посредством связей структуры G).

2. Программируемость структуры (изменение структуры G на основе программного управления).

3. Однородность конструкции H (однородности вычислителей C = {ci} и структуры G).

Алгоритм A работы коллектива S обеспечивает работу всех вычислителей C = {ci} и структуры G в процессе решения общей задачи. Данный алгоритм может быть представлен в виде суперпозиции

A(P(D)),                                                (3)

где D – исходный массив данных, подлежащих обработке в процессе решения задачи.

В свою очередь,

                                              (4)

где Di – индивидуальный массив данных для вычислителя ci ϵ C.

Причем в общем случае

                                              (5)

где P – параллельная программа решения общей задачи.

Параллельная программа может быть представлена в виде нескольких ветвей програм- мы:

                              (6)

где Pi – i-я ветвь программы P.

Особенности представления структуры суперкомпьютера

Структура суперкомпьютера должна представлять собой программно-неделимый ап- паратный ресурс при организации вычислительного процесса. Поэтому формирование структуры суперкомпьютера целесообразно производить по принципу модульной наращиваемости из однотипных базовых модулей – вычислительных кластеров (ВК), которые, с одной стороны, имеют конструктивные ограничения, а с другой, должны формироваться для конкретных военно-прикладных задач.

Каждый ВК включает некоторое сбалансированное количество элементарных процессоров (ЭП) и блоков памяти, объединенных с помощью полнодоступной системы быстрых каналов и способных реализовать, желательно целиком, базовые наборы различных задач.

Схематически общая структурная схема ВК изображена на рисунке 1.

Структура суперкомпьютера в целом должна формироваться по принципу модульной наращиваемости путем объединения нескольких ВК с помощью коммутационной среды К2, соблюдая принцип иерархичности. Данный принцип позволяет увеличить производительность суперкомпьютера при увеличении количества ВК. В состав суперкомпьютера могут входить разнотипные ВК, а также интерфейсы (I1, ..., Iq) внешних вычислительных ресурсов, связанных с суперкомпьютером.

Схематически структурная схема суперкомпьютера изображена на рисунке 2.

Каждый вариант структуры суперкомпьютера представляет собой совокупность аппаратных и программных ресурсов и математически описывается следующим образом.

В основе варианта лежит элемент множества U, который представляет собой вектор параметров:

Ui = <(Gk)i, (Gp)i>, i = 1(1)O(U),               (7)

где Gk – совокупность аппаратных ресурсов уровня суперкомпьютера (ВК и связей между ними); Gр – совокупность аппаратных ресурсов уровня ВК (ЭП и связей между ними).

В свою очередь, (Gk)i представляет собой следующий вектор параметров:

(Gk)i = <(Nk)i, (Sk)i, (Mkcom)i>, i = 1(1)O(U),      (8)

где Nk – количество ВК, входящих в состав суперкомпьютера; Mkcom – тип устройства межкластерной коммуникации; Sk – матрица смежности графа, описывающего структуру связей между ВК.

Sk представляет собой симметричную квадратную матрицу размером Nk ˣ Nk неориентированного графа, описывающего структуру связей ВК между собой. Данная матрица формируется следующим образом:

(9)

где i, j = 1(1)Nk – количество ВК, входящих в состав суперкомпьютера.

Каждый элемент (Gp)i представляет собой следующий вектор параметров:

(Gp)i = <(Mu)i, (Nu)i, (Ms)i, (Ns)i, (Mрcom)i, (Sр)i>, i = 1(1)O(U),                       (10)

где Mu – тип универсального процессора, входящего в состав каждого ВК; Nu – количество универсальных процессоров, входящих в состав каждого ВК; Ms – тип специализированного процессора, входящего в состав каждого ВК; Ns – количество специализированных процессоров, входящих в состав каждого ВК; Mрcom – тип среды межпроцессорной коммуникации; Sр – матрица смежности графа, описывающего структуру связей между специализированными процессорами в составе каждого ВК.

Sр представляет собой симметричную квадратную матрицу размером Ns ˣ Ns неориентированного графа, описывающего структуру связей между специализированными процессорами в составе каждого ВК. Данная матрица формируется следующим образом:

   (11)

где i, j = 1(1)Ns.

Формирование множества вариантов структуры суперкомпьютера осуществляется в следующей последовательности.

1. Генерируется множество допустимых вариантов структур связей между ВК.

2. Генерируется множество допустимых вариантов структур связей между ЭП в составе ВК.

3. Формируется множество допустимых вариантов устройств межпроцессорной коммуникации, совместимых с ЭП.

4. Формируется множество комбинаций для описанных выше элементов.

Генерация множества допустимых вариантов структур связей между ВК, а также процессорами в составе ВК сводится к формированию матриц Sk и Sр. Данная задача относится к классу комбинаторных задач. Поскольку Sk и Sр являются матрицами смежности неориентированных графов, в силу их симметричности относительно главной диагонали можно вычислить зависимость числа сгенерированных комбинаций от числа ВК по формуле

,                                          (12)

где М – число сгенерированных вариантов; N – число комбинируемых ВК.

ВК должны быть связаны между собой ка- кой-либо коммуникационной средой. Данное условие математически определяется свойством связности графа, описывающего структуру суперкомпьютера.

Проверка связности некоторого графа G с вершинами v1, v2, …, vn и матрицей смежности A осуществляется на основе проверки условия

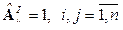,                                  (13)

здесь ,         (14)

где I – единичная мультипликативная матрица;  – операция булева произведения матриц [12].

Для математического описания структуры вычислительной системы, как правило, используют матрицу смежности. Однако матрица смежности не может служить исчерпывающим описанием структуры суперкомпьютера, поскольку жестко привязывается к нумерации вершин. Это приводит к тому, что некоторые одинаковые по топологии варианты структуры суперкомпьютера, графы которых изоморфны, обладают отличными матрицами смежности. Данное обстоятельство обусловливает необходимость распознавания изоморфизма и изоморфного вложения сложных структур, заданных в форме матриц или графов.

С содержательной точки зрения изоморфизм структур означает тождественность их функционирования, что в некоторых случаях приводит к возможности замены одной структуры другой, изоморфной ей. Однако для распознавания изоморфизма применяется алгоритм полного перебора, что делает проблему изоморфизма практически нерешаемой уже при сравнительно небольшом числе элементов данной структуры. Легко видеть, что для распознавания изоморфизма графов, которые имеют n вершин, требуется в общем случае выполнить n! попарных сравнений, то есть при относительно небольшом количестве элементов в графах (около 100) решение задачи об изоморфизме методом полного перебора невозможно.

Для решения задачи определения изоморфизма графов в качестве топологической характеристики графа, инвариантной к нумерации его вершин, предлагается использовать спектр графа.

Спектр отражает общие свойства всех тех графов, матрицы смежности которых преобразуются друг в друга посредством некоторой невырожденной матрицы [9].

Обыкновенным спектром графа G называют спектр его матрицы смежности A.

Использование спектра графа обусловлено следующим. Каждому графу G однозначно соответствует класс A = A(G) матриц смежности. Две матрицы смежности A и A' определяют один и тот же граф тогда и только тогда, когда существует такая матрица перестановки P, что A = P-1AP. Следовательно, важным инвариантом класса A является

SP(G) = {λ1, λ2, …, λn},                         (15)

где λi – корни уравнения PG(λ) = 0.

Таким образом, для определенного класса графов с ограничением на количество вершин и на имеющиеся сведения о неизоморфных коспектральных графах возможно решение задачи определения изоморфизма графов на основе использования одного из инвариантов графов – их спектров [9, 13, 14].

Вычисление спектра графа по сути своей является определением собственных значений его матрицы смежности. Существуют следующие методы вычисления.

1. Метод непосредственного развертывания, который используется для вычисления собственных значений матриц невысокого порядка (n ≤ 10). Вычислительная сложность алгоритма, реализующего данный метод, описывается порядком O(n3) при решении задачи развертывания дискриминанта и O(log2n) при условии решения нелинейных уравнений методом дихотомии. Таким образом, сложность алгоритма составляет порядка O(n3).

2. Метод итераций, который применяется для решения частичной проблемы собственных значений матрицы (на его основе можно определить приближенно собственные значения матрицы). Вычислительная сложность алгоритма, реализующего данный метод, описывается порядком O(2n(n + 1)L). Здесь L – количество итераций алгоритма, зависящее от установленной точности вычислений.

Очевидно, что даже такая высокая вычислительная сложность реализуемых алгоритмов является более предпочтительной, чем сложность О(n!), соответствующая алгоритму полного перебора.

Алгоритм формирования множества вариантов структуры суперкомпьютера

Для формирования множества вариантов структуры суперкомпьютера разработан оригинальный алгоритм, основанный на использовании свойств спектра графа.

Исходные и выходные данные разработанного алгоритма представлены в таблице.

Ωu и Ωs представляют собой симметричные матрицы относительно главной диагонали размером O(Mu) ˣ O(Mpcom), O(Ms) ˣ O(Mpcom) соответственно. Они формируются следующим образом:

(16)

где i = 1(1)O(Mu), j = 1(1)O(Mpcom).

(17)

где i = 1(1)O(Ms), j = 1(1)O(Mpcom).

В качестве ограничений и допущений при разработке настоящего алгоритма рассматриваются следующие:

–     все ВК осуществляют обработку информации параллельно и имеют непосредственную или косвенную связь друг с другом на основе общей магистрали (граф, описывающий структуру суперкомпьютера, является связным);

–     каждый ВК должен представлять собой объединение однородных специализированных процессоров, находящихся под управлением одного или нескольких универсальных процессоров;

–     все ЭП в составе ВК имеют непосредственную или косвенную связь друг с другом (граф, описывающий структуру ВК, является связным).

Алгоритм (см. http://www.swsys.ru/upload ed/image/2019-4/2019-4-dop/1.jpg) предполагает выполнение следующих шагов.

Шаг 1. Ввод исходных данных.

Шаг 2. Начало цикла по .

Шаг 3. Генерация матрицы смежности (Sk)i.

Шаг 4. Расчет матрицы  для выявления свойства связности графа.

Шаг 5. Проверка свойства связности графа . Если данное условие выполняется, то осуществляется переход к шагу 6, в противном случае – к шагу 10.

Шаг 6. Расчет спектра SP(Sk)i матрицы смежности (Sk)i графа.

Шаг 7. Проверка факта совпадения рассчитанного спектра SP(Sk)i со спектром одного из выбранных ранее графов. Если данное условие выполняется, осуществляется переход к шагу 8, в противном случае – к шагу 9.

Шаг 8. Проверка того, относится ли граф с матрицей смежности (Sk)i к исключениям – семействам коспектральных неизоморфных гра- фов или нет. Если данное условие выполня- ется, осуществляется переход к шагу 9, в противном случае – к шагу 10.

Шаг 9. Добавление (Sk)i в множество допустимых вариантов .

Шаг 10. Конец цикла по i.

Шаг 11. Начало цикла по .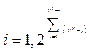

Шаг 12. Генерация матрицы смежности (Sp)i графа.

Шаг 13. Расчет матрицы  для проверки связности графа, описывающего структуру ВК.

Шаг 14. Проверка свойства связности графа, описывающего структуру суперкомпьютера: ; l, m = 1(1)Nвк. Если данное условие выполняется, осуществляется переход к шагу 15, в противном случае – к шагу 19.

Шаг 15. Расчет SP((Sp)i) – спектра матрицы смежности (Sp)i графа, описывающего структуру ВК.

Шаг 16. Проверка факта совпадения рассчитанного спектра SP((Sp)i) со спектром одного из выбранных ранее графов. Если данное условие выполняется, осуществляется переход к шагу 17, в противном случае – к шагу 18.

Шаг 17. Проверка, относится ли граф с матрицей смежности (Sp)i к исключениям – семействам коспектральных неизоморфных графов. Если данное условие выполняется, осуществляется переход к шагу 18, в противном слу- чае – к шагу 19.

Шаг 18. Добавление (Sp)i в множество допустимых вариантов структуры ВК S¢p.

Шаг 19. Конец цикла по i.

Шаг 20. Выбор процессора общего назначения из множества Mu.

Шаг 21. Начало цикла по i = 1(1)O(Mpcom).

Шаг 22. Проверка совместимости выбранного процессора общего назначения с (Mpcom)i устройством межпроцессорной коммуникации: (Ωu)ki = 1, k – номер элемента из множества Mu. Если данное условие выполняется, осуществляется переход к шагу 23, в противном случае – к шагу 24.

Шаг 23. Добавление (Mpcom)i в множество допустимых вариантов структуры ВК M¢pcom.

Шаг 24. Конец цикла по i.

Шаг 25. Проверка, является ли множество M¢pcom пустым (M¢pcom = Æ). Если данное условие выполняется, осуществляется переход к шагу 20, в противном случае – к шагу 26.

Шаг 26. Выбор процессора общего назначения из множества Ms.

Шаг 27. Начало цикла по i = 1(1)O(M¢pcom).

Шаг 28. Проверка совместимости выбранного процессора общего назначения с (M¢pcom)i устройством межпроцессорной коммуникации: (Ωs)ki = 1, k – номер элемента из множества Ms. Если данное условие выполняется, осуществляется переход к шагу 29, в противном случае – к шагу 30.

Шаг 29. Добавление (M¢pcom)i в множество допустимых вариантов структуры ВК M¢¢pcom.

Шаг 30. Конец цикла по i.

Шаг 31. Проверка, является ли множество M¢¢pcom пустым (M¢¢pcom = Æ). Если данное условие выполняется, осуществляется переход к шагу 26, в противном случае – к шагу 32.

Шаг 32. Начало цикла по i = 1(1)O(S¢k).

Шаг 33. Начало цикла по j = 1(1)O(Mkcom).

Шаг 34. Начало цикла по k = 1(1)O(S¢p).

Шаг 35. Начало цикла по l = 1(1)O(M¢¢pcom).

Шаг 36. Начало цикла по m = 1(1)O(Mram).

Шаг 37. Формирование элемента множества вариантов структуры суперкомпьютера U.

Шаг 38. Конец цикла по m.

Шаг 39. Конец цикла по l.

Шаг 40. Конец цикла по k.

Шаг 41. Конец цикла по j.

Шаг 42. Конец цикла по i.

Шаг 43. Вывод результатов.

Таким образом, представленный алгоритм, в отличие от существующих, позволяет рассматривать процесс формирования множества вариантов структур суперкомпьютеров как многоитерационную рекурсивную процедуру, применяющую обобщенный набор операций для представления вычислительных модулей на любом уровне абстракции в виде вычислительных кластеров. При этом важную роль играет использование спектра графа при генерации множества структур связей между вычислительными кластерами, а также элементарными процессорами в составе вычислительных кластеров.

Заключение

Практическая значимость разработанного алгоритма заключается в том, что он может быть реализован в виде программного модуля на языке программирования высокого уровня в качестве составной части ПО, предназначенного для проектирования многопроцессорных вычислительных систем специального назначения. Применение разработанного алгоритма в процессе проектирования суперкомпьютеров специального назначения позволит значительно снизить вычислительные затраты на моделирование множества допустимых вариантов структур вычислительных систем при определении факта изоморфизма и изоморфного вложения графов. В результате разработанный алгоритм может быть использован для обоснования архитектурных решений при создании новых суперкомпьютеров и выделения вычислительных ресурсов под решение военно-прикладных задач на существующих суперкомпьютерах.

Литература

1.    Буренок В.М., Гладышевский В.Л. Информатика и вычислительная техника: перспективы развития и применения в военном деле // Вооружение и экономика. 2015. № 3. С. 17–32.

2.    Адамов А.А., Фомин Д.В., Эйсымонт Л.К. Главные проблемные направления в области отечественной элементной базы суперкомпьютеров // Вопросы кибербезопасности. 2019. № 4. С. 2–12. DOI: 10.21681/2311-3456-2019-4-02-12.

3.    Леоненков С.Н. Целевая оптимизация структуры потока задач суперкомпьютеров // Вычислительные методы и программирование: новые вычислительные технологии. 2019. Т. 20. № 3. С. 199–210. DOI: 10.26089/NumMet.v20r319.

4.    Лушников Н.Д. СуперЭВМ как высокопроизводительное аппаратно-техническое средство функционирования в среде виртуальной реальности // Перспективы науки. 2019. № 1. С. 22–24.

5.    Назаров С.В., Барсуков А.Г. Организация вычислительного процесса в суперкомпьютерах с динамически управляемыми разделами // Современные информационные технологии и ИТ-образование. 2019. Т. 15. № 1. С. 59–71. DOI: 10.25559/SITITO.15.201901.59-71.

6.    Петрич Д.О., Гусеница Я.Н., Завалишин М.А. Научно-методический подход к выбору рационального варианта архитектуры вычислительного комплекса радиолокационной системы специального назначения // Тр. ВКА им. Можайского. 2011. № 632. С. 50–55.

7.    Рябов Г.Г., Сургуладзе М.Ш. Суперкомпьютер и дискретная топология // Тр. НИИСИ РАН. 2018. Т. 8. № 1. С. 44–47. DOI: 10.25682/NIISI.2018.1.0007.

8.    Цветкович Д., Дуб М., Хахс X. Спектры графов. Теория и применение. К.: Наук. думка, 1984. 383 с.

9.    Хорошевский В.Г. Архитектура вычислительных систем. М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. 520 с. URI: http://www.nsu.ru/xmlui/handle/nsu/935 (дата обращения: 05.09.2019).

10. Авен О.И., Гурин Н.Н., Коган Я.А. Оценка качества и оптимизация вычислительных систем. М.: Наука, 1982. 464 с.

11. Вейцман К. Распределенные системы мини- и микро-ЭВМ. М.: Финансы и статистика, 1983. 382 с.

12. Хаггарти Р. Дискретная математика для программистов. М.: Техносфера, 2018. 400 с.

13. Андреев А.М., Модаров Г.П., Сюзев В.В. Многопроцессорные вычислительные системы: теоретический анализ, математические модели и применение. М.: Изд-во МГТУ им. Н.Э. Баумана, 2011. 332 с.

14. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. 416 с.

References

1. Burenok V.M., Gladyshevsky V.L. Informatics and computing: prospects for development and military application. Armament and Economics. 2015, no. 3, pp. 17–32 (in Russ.).
2. Adamov A.A., Fomin D.V., Eysymont L.K. The main problem areas in the field of the domestic element base of supercomputers. Cybersecurity Issues. 2019, no. 4, pp. 2–12. DOI: 10.21681/2311-3456-2019-4-02-12 (in Russ.).
3. Leonenkov S.N. Target optimization of the of the supercomputer task flow structure. Numerical Methods and Programming. 2019, vol. 20, no. 3, pp. 199–210. DOI: 10.26089/NumMet.v20r319 (in Russ.).
4. Lushnikov N.D. Supercomputers as a high-performance hardware-technical mean of functioning in a virtual reality environment. Science Prospects. 2019, no. 1, pp. 22–24 (in Russ.).
5. Nazarov S.V., Barsukov A.G. Organization of the computational process in supercomputers with dynamically controlled partitions. Modern Information Technologies and IT Education. 2019, vol. 15, no. 1, pp. 59–71. DOI: 10.25559/SITITO.15.201901.59-71 (in Russ.).
6. Petrich D.O., Gusenitsa Ya.N., Zavalishin M.A. Scientific and methodological approach to the selection of a rational version of the computing complex architecture of a special-purpose radar system. Proc. of the Mozhaisky Military Aerospace Academy. 2011, no. 632, pp. 50–55 (in Russ.).
7. Ryabov G.G., Surguladze M.Sh. Supercomputer and discrete topology. Proc. SRISA RAS. 2018, vol. 8, no. 1, pp. 44–47. DOI: 10.25682/NIISI.2018.1.0007 (in Russ.).
8. Cvetkovich D., Dub M., Hahs X. Graphs Spectra. Theory and Application. Kiev, Nauk. dumka Publ., 1984, 383 p.
9. Horoshevsky V.G. Computer Architecture. Moscow, MSTU Publ., 2008, 520 p. Available at: http://www.nsu.ru/xmlui/handle/nsu/935 (accessed September 05, 2019).
10. Aven O.I., Gurin N.N., Kogan Ya.A. Quality Assessment and Optimization of Computing Systems. Moscow, Nauka Publ., 1982, 464 p.
11. Vejcman K. Distributed Mini and Microcomputer Systems. Moscow, Finansy i statistika Publ., 1983, 382 p.
12. Haggarti R. Discrete Math for Programmers. Moscow, Tekhnosfera Publ., 2018, 400 p.
13. Andreev A.M., Modarov G.P., Syuzev V.V. Multiprocessor Computing Systems: Theoretical Analysis, Mathematical Models and Applications. Moscow, Bauman MSTU Publ., 2011, 332 p.
14. Geri M., Dzhonson D. Computing Machines and Difficult Tasks.  Moscow, Mir Publ., 1982, 416 p.