Жизненный цикл разработки и производства новых или модификации уже используемых лекарственных препаратов очень длительный и дорогой. Прежде чем разработанное лекарственное средство будет допущено в промышленное производство, оно 12–15 лет проходит доклинические, клинические и предпроизводственные испытания. В них участвуют специалисты многих областей – биологи, медики, технологи, химики, математики, программисты.
 На стадии клинических испытаний могут быть задействованы тысячи человек, на кото- рых проверяется разрабатываемое лекарствен- ное средство, и десятки, а порой и сотни специалистов, занятых статистической и медико-биологической обработкой данных проводимых исследований. Отсюда понятно, какую важную роль играет начальный этап жизненного цикла – синтез и химико-технологическая разработка лекарственного средства [1, 2], когда не только закладываются все биологические и химико-технологические свойства разрабатываемого лекарственного средства, но и формируется технологическая платформа для его дальнейшего производства и выбирается оборудование. Столь важная роль этапа разработки, разнообразие применяемых при этом различными группами исследователей методов и средств обусловили то, что на сегодня из всего жизненного цикла лекарственного средства единственным несертифицированным этапом осталась именно разработка (рис. 1) [3].
На стадии клинических испытаний могут быть задействованы тысячи человек, на кото- рых проверяется разрабатываемое лекарствен- ное средство, и десятки, а порой и сотни специалистов, занятых статистической и медико-биологической обработкой данных проводимых исследований. Отсюда понятно, какую важную роль играет начальный этап жизненного цикла – синтез и химико-технологическая разработка лекарственного средства [1, 2], когда не только закладываются все биологические и химико-технологические свойства разрабатываемого лекарственного средства, но и формируется технологическая платформа для его дальнейшего производства и выбирается оборудование. Столь важная роль этапа разработки, разнообразие применяемых при этом различными группами исследователей методов и средств обусловили то, что на сегодня из всего жизненного цикла лекарственного средства единственным несертифицированным этапом осталась именно разработка (рис. 1) [3].
Методологическую основу предлагаемой разработки составляет системная реализация принципа QbD на стадии разработки непрерывного синтеза активного фармацевтического ингредиента (АФИ).
Согласно [4], Quality-by-Design (QbD) – это системный подход к разработке лекарственных препаратов, который начинается с четко определенных целей и заканчивается получением лекарственного препарата, а также включает анализ процесса изготовления и стратегии контроля, основываясь на надежных научных данных и оценке рисков, связанных с качеством готовой продукции (см. таблицу).

 Главным принципом концепции QbD является концентрация основной цели разработки на готовом продукте и его потребителе (пациенте). Это связано прежде всего с оценкой рисков применения новой разработки для потребителей. Причем только в обратном порядке по ходу разработки устраняются все возможные производственные опасности, связанные с применяемым сырьем и технологией процесса.
Главным принципом концепции QbD является концентрация основной цели разработки на готовом продукте и его потребителе (пациенте). Это связано прежде всего с оценкой рисков применения новой разработки для потребителей. Причем только в обратном порядке по ходу разработки устраняются все возможные производственные опасности, связанные с применяемым сырьем и технологией процесса.
Поэтому реализация подхода QbD включает решение следующих основных задач [5]:
- определение критических свойств лекарственного препарата (исходя из его целевого профиля);
- определение критических параметров технологического процесса и характера влияния их изменчивости на качество готовых лекарственных форм (ГЛФ);
- определение пространства разработки или, как иногда называют, области проектных решений (Design Space);
- формирование стратегии контроля качества.
Соответственно, еще на ранних этапах разработки с помощью методологии оценки рисков (выявление вреда, вероятности его возникновения и тяжести последствий) можно спрогнозировать критические показатели для продукта и критические параметры процесса. По мере получения новых знаний и экспериментальных данных на последующих этапах разработки, при переносе технологии и масштабировании производства, по результатам валидации эта оценка будет только уточняться.
Для выбора критических параметров качества и критических показателей процесса используются научное обоснование и методология оценки рисков. Это связано с тем, что между риском и критичностью есть прямая  связь, так как риск включает тяжесть вреда, вероятность развития и выявляемость его с помощью применяемых средств контроля. Таким образом, управление риском позволяет снизить уровень его критичности от неприемлемого до серьезного и далее до незначительного.
связь, так как риск включает тяжесть вреда, вероятность развития и выявляемость его с помощью применяемых средств контроля. Таким образом, управление риском позволяет снизить уровень его критичности от неприемлемого до серьезного и далее до незначительного.
Согласно определению [5], функции QbD включают две основные составляющие: формирование критерия CQA (critical quality attribute) – это химический, микробиологический или биологический показатель, у которого имеется некоторое предельное значение, обеспечивающее заданное качество, и математическое моделирование процесса синтеза. Наиболее часто в данном случае используется регрессионный анализ, при этом параметры CQA становятся целевыми функциями или откликами. Основополагающие идеи, сформулированные в принципе QbD, положены авторами в основу построения алгоритмов управления непрерывным синтезом при фармацевтической разработке лекарственных веществ [6].
В качестве критериев задан спектр условий, в которых предстоит выполнять исследования, и применительно к каждому условию качество функционирования оценивается самостоятельным критерием. При решении проблемы разработки лекарственных средств группы экспертов на каждом этапе жизненного цикла вносят коррективы в первоначально заданный глобальный критерий, формируя локальные критерии [7].
Глобальный критерий G может быть определен множеством частных критериев Kjm:
 ,(1)
,(1)
где Sim – элемент некоторой формальной модели; f P– функция отображения; N – число введенных частных критериев; Djm – множество атрибутов частного критерия (наименование, описание и т.д.).
При этом выбор принципа оптимальности управленческого решения всегда зависит от предпочтений ЛПР, а также от особенностей поставленной задачи. Однако в практических задачах достаточно часто возникает ситуация, когда часть критериев нужно максимизировать, а часть минимизировать. В этом случае для оценки критерия оптимизации  можно использовать соотношение
можно использовать соотношение
Optim G = min[∑kui +(∑kui)-1], (2)
где kiu, i = 1, …, l – локальные критерии, которые необходимо максимизировать; kui, i = 1, …, h – локальные критерии, которые необходимо минимизировать.
 В задачах разработки лекарственных средств минимизируются глобальный и локальные критерии риска, а максимируются критерии качества и стоимости готового препарата. Схема формирования глобального критерия представлена на рисунке 2.
В задачах разработки лекарственных средств минимизируются глобальный и локальные критерии риска, а максимируются критерии качества и стоимости готового препарата. Схема формирования глобального критерия представлена на рисунке 2.
Этап фармацевтической разработки ГЛФ состоит из двух подэтапов – синтеза АФИ и разработки состава ГЛФ [8]. Разработка и промышленная реализация этих подэтапов достаточно автономны, и в большинстве случаев промышленные предприятия синтеза и производства состава находятся в разных местах.
Однако в последнее время за рубежом появились экспериментальные разработки технологий, объединяющих в едином непрерывном потоке синтез и разработку состава ГЛФ [9]. Такие разработки стали возможными в связи с появлением новых материалов, внедрением в практику нанотехнологий и широким исполь- зованием информационных технологий. Технология реакторов с непрерывным потоком вызвала значительный интерес из-за ряда серьезных преимуществ, которые она предлагает по сравнению с традиционными периодическими процессами, таких как значительное снижение технологических затрат и повышение эффективности процесса. Преимущества обусловлены быстрым перемешиванием, хорошей теплопередачей, безопасной работой при высоких температурах, а также возможностью полной компьютеризации управления процессом. Эти функции обеспечивают возможность проведения органических реакций и очистки со скоростями, недостижимыми при периодической схеме синтеза.
В [10] для комплексного управления непрерывным синтезом и производства твердых лекарственных форм была разработана автоматическая компьютерная система, функционирующая как на стадии исследований, так и при нормальной эксплуатации установки. Архитектура разработанной системы, а также алгоритмы и программные средства управления в статье не раскрыты. Рассматриваемая далее интеллектуальная система подготовки управленческих решений не содержит инструментальных средств автоматического управления процессом – она предназначена для формирования в режиме on-line рекомендаций исследователю, проводящему синтез АФИ.
Рассмотрим методику построения программно-алгоритмичекого обеспечения системы интеллектуального управления на примере непрерывного синтеза конкретного лекарственного средства дифенгидрамина (димедро- ла) [11].
Димедрол получают взаимодействием бензгидрола (I) и β-диметиламиноэтилхлорида в спиртовом растворе алкоголята натрия [8] или реакцией I и гидрохлорида β-диметиламиноэтилхлорида (II); в присутствии едкого натра с последующим превращением основания III в гидрохлорид – димедрол (IV) (рис. 3).


 Диаграммы информационного моделирования процесса синтеза дифенгидрамина в нотации IDEF0 представлены на рисунках 4 и 5. Они позволяют отследить информационные связи между отдельными стадиями процесса синтеза, а также с применяемой в процессе контрольно-измерительной аппаратурой.
Диаграммы информационного моделирования процесса синтеза дифенгидрамина в нотации IDEF0 представлены на рисунках 4 и 5. Они позволяют отследить информационные связи между отдельными стадиями процесса синтеза, а также с применяемой в процессе контрольно-измерительной аппаратурой.
На рисунке 5 представлена информационная модель непрерывного синтеза в нотации IDEF0.
 Информационная модель является основой построения информационной поддержки системы непрерывного синтеза. Для управления процессом исследований предлагается интеллектуальная система, в состав которой входят БД, подсистема поддержки управленческих решений и ряд других подсистем сбора и обработки информации (рис. 6) [12].
Информационная модель является основой построения информационной поддержки системы непрерывного синтеза. Для управления процессом исследований предлагается интеллектуальная система, в состав которой входят БД, подсистема поддержки управленческих решений и ряд других подсистем сбора и обработки информации (рис. 6) [12].
Построение большинства модулей интеллектуальной системы достаточно подробно описано в литературе [13, 14], поэтому далее будет рассмотрено только алгоритмическое и программное обеспечение оригинальных модулей системы – подсистем моделирования и оптимизации и подготовки управленческих решений для исследователя. Сформулируем за- дачу математического моделирования про- цесса непрерывного синтеза АФИ димедрола.
Итак, необходимо построить регрессионную модель зависимости критерия G(x1, x2, x3) от управляемых параметров x1, x2, x3. В качестве критерия оптимизации G используются степень извлечения при синтезе:
G(xi1, xi2, xi3) = a1*xi1 + a2*xi2 + a3*xi3
(i = 1, 2, 3, …, n) (3)
и регрессионные модели для измерямых, но неуправляемых параметров, служащих ограничениями изменений управляемых параметров:
Yj(xi1, xi2, xi3) ≤ Yjдоп., (4)
где x1, x2, x3 – соответственно значения температуры (t °C), время (мин.) и заместитель в ингредиентах Br или Cl; Yj(x1, x2, x3) – ограничения, определяющие состав или структуру получаемого соединения и измеряемые хроматографом.
Если регрессионное уравнение (3) построить достаточно просто, то для построения уравнений (4) предлагается использовать методику построения многооткликового регрессионного уравнения.
 Запишем уравнение многооткликового уравнения регрессии для моделирования процесса получения веществ 1, 6, 7 (рис. 6 ) в матричной форме:
Запишем уравнение многооткликового уравнения регрессии для моделирования процесса получения веществ 1, 6, 7 (рис. 6 ) в матричной форме:
A = (X*Xt)-1 *(Xt *Y), (5)
где верхние индексы t и -1 обозначают операции транспонирования и обращения матриц соответственно; A – вектор-столбец регрессионных коэффициентов; X – матрица управляемых параметров x1, x2, x3; Y – матрица целевых показателей y1, y2, y3:
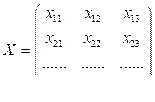 ;
; ;
;
 . (6)
. (6)
Решением матричного уравнения (3) является матрица A, где каждый из коэффициентов akj соответствует регрессионному уравнению с целевой функцией Yk (k = 1, 2, 3).
Отметим, что в уравнениях (1)–(3) индекс i относится к номеру эксперимента, индекс j к номеру коэффициента в регрессионном уравнении, индекс k к номеру целевой функции в критериальных уравнениях ограничений (2). Yjдоп. – допустимые значения компонентов состава, задаваемые до начала процесса синтеза.
Программная реализация алгоритма моделирования выполнена на свободно распространяемом программном кроссплатформенном комплексе Scilab (Scilab Enterprises) [15], имеющем, благодаря свободному доступу, существенное преимущество перед коммерческим программным продуктом Matlab (Mathworks Corp.). Scilab предназначен, главным образом, для инженерных расчетов, имеет удобный пользовательский интерфейс и хорошие возможности визуализации полученных резуль- татов. Однако этот комплекс не содержит подпрограммы для регрессионного анализа сложных многооткликовых множественных уравнений, хотя запись системы регрессионных уравнений в матричной форме позволяет найти решение достаточно просто, так как Scilab обладает необходимым набором операций работы с матрицами.
Построенные регрессионные уравнения дают возможность решать на втором этапе задачу оптимизации. Целью этого этапа является построение алгоритма online-оптимизации, когда на каждом шаге определяется такой план изменения управляемых переменных x1, x2, x3, при котором значения G извлечения в процессе синтеза растут, а ограничения (2) не выходят за пределы допустимых: Yj(xi1, xi2, xi3) ≤ Yjдоп..
В качестве алгоритма оптимизации может быть выбран практически любой пошаговый метод, например, метод крутого восхождения. Однако, если количество управляемых переменных больше двух и корреляционная матрица в регрессионном уравнении недиагональна, организовать движение по градиенту становится несколько затруднительно. Кроме того, особенностью предлагаемой процедуры поиска оптимума является включение исследователя в контур алгоритма управления. Поэтому была выбрана одна из модификаций покоординатного поиска оптимума – алгоритм Хука–Дживса [16].
Остановимся подробнее на алгоритме, реа- лизуемом в подсистеме информационной под- держки управленческих решений при определении оптимальных параметров различных стадий в системе непрерывного синтеза димедрола.
Общее уравнение решения задачи оптимизации имеет следующий вид:
G = b1*x1 + b2*x2 + b3*x3 →max, (7)
где G – критерий оптимизации (показатель конверсии); x1, x2, x3 – управляемые параметры процесса непрерывного синтеза.
Если представить контролируемые параметры в виде ограничений, то задача оптимизации примет вид
G = b1*x1 + b2*x2 + b3*x3 →max, (8)
Yik = ᴪj(x1, x2, …, xn) ≤ abs(Yiдоп.k), (9)
где abs(Yiдоп.k) определяется нормативными требованиями на ограничения по этому параметру.
В работе выбран двухступенчатый подход к решению задачи оптимизации: на первом выполняется пошаговое движение к оптимуму, на втором для найденного плана управляемых переменных проводится проверка допустимых значений состава. Такой подход позволяет экономить время и ресурсы за счет отказа от планов, при которых возможно нарушение ограничений по составу. Для решения задачи оптимизации выбран один из методов покоординатного движения. Используем для этого модифицированный метод Хука–Дживса.
Метод относится к большому семейству методов покоординатного поиска и включает два этапа: сканирующий поиск вокруг некоторой точки, определяемой после цикла поиска в качестве базисной, и организация движения от базисной точки по направлению к экстремуму (максимуму в нашей задаче) – так называемый поиск по образцу.
На начальном этапе задаются стартовая точка (обозначим ее x0) и шаги ∆xi по координатам. Затем замораживаются значения всех координат, кроме 1-й, вычисляются значения функции в точках x0 + ∆x0 и x0 – ∆x0 (где x0 – первая координата точки, а ∆x0 – соответственно значение шага по этой координате) и осуществляется переход в точку с наибольшим значением функции. В этой точке замораживаются значения всех координат, кроме 2-й, вычисляются значения функции в точках x1 + ∆x1 и x1 – ∆x1. Если приращение улучшает целевую функцию, то шаг считается удачным; по этой переменной значение изменяется на величину шага и дается приращение по другой переменной. В противном случе – неудачным и де- лается шаг в противоположном направле- нии, и т.д. для всех координат. Затем через две точки, характеризующие наибольшие увеличения целевой функции, проводится линия направления движения. Метод Хука–Дживса имеет много алгоритмов, отличающихся по существу организацией движения на 2-м этапе, то есть поиском по образцу.
Программный комплекс Scilab не содержит процедур многомерной оптимизации, поэтому авторами была разработана программная реализация одного из алгоритмов метода Хука–Дживса:
function res = myfunc(x)
res = 8*(x(1,1)^2) + 4*x(1,1)*x(1,2) + 5*(x(1,2)^2);
end
clear all;
n=input('Введите кол-во координат:');
e=0.0001;% параметр окончания поиска
h=1; % шаг
% ввод базовых координат
x=zeros(1,n);
fori=1:n
x(1,i)=input ([sprintf('Введите значение базовой координаты %g',i) ': ']);
end
% берем базисную точку и вычисляем значение функции в ней
xb=x;
rb=myfunc(xb);
while (h > e)
disp('Шаг ');
disp(h);
disp('проводим исследование ');
% проводим исследование, нам нужны временные переменные
x=xb;
r=rb;
% по координатам
x1=x;
for i=1:n
x1(1,i) = x(1,i) + h;
r1 = myfunc (x1);
if (r1 < r)
x = x1;
r = r1;
else
x1(1,i) = x(1,i) - h;
r1 = myfunc (x1);
if (r1 < r)
x = x1;
r = r1;
end
end;
end;
disp('завершили исследование ');
% проверяем текущее значение и значение в базисной точке на меньше
if (r < rb)
while(1)
*далее алгоритм вычисления повторяется для новой точки
 Отметим особенности предложенного алгоритма. Метод Хука–Дживса предназначен для поиска локального экстремума. Попытка найти глобальный экстремум может быть предпринята, если запускать поиск из разных точек факторного пространства. Принципиально метод относится к методам безусловной оптимизации. Для учета ограничений предлагается в контур работы алгоритма включить исследователя, который проверяет выполнение ограничений на каждом шаге поиска или через несколько шагов. По существу предлагаемый алгоритм является человеко-машинным: компьютер просчитывает план организации движения к оптимуму, а решение о выполнении этого плана пошагово принимает исследователь.
Отметим особенности предложенного алгоритма. Метод Хука–Дживса предназначен для поиска локального экстремума. Попытка найти глобальный экстремум может быть предпринята, если запускать поиск из разных точек факторного пространства. Принципиально метод относится к методам безусловной оптимизации. Для учета ограничений предлагается в контур работы алгоритма включить исследователя, который проверяет выполнение ограничений на каждом шаге поиска или через несколько шагов. По существу предлагаемый алгоритм является человеко-машинным: компьютер просчитывает план организации движения к оптимуму, а решение о выполнении этого плана пошагово принимает исследователь.
Далее рассмотрим алгоритм оптимизации управления синтезом димедрола (рис. 7).
Разработанные алгоритмы были применены для построения оптимальных планов исследований, проводимых на уникальной микрореакторной установке Qmix. В качестве исходных компонентов использовался хлорбензогидрол или бромбензогидрол. Условия: T (°C) = = 100–180, время реакции t (мин.) = 2–20. Состав полученной смеси измерялся с помощью высокоэффективной жидкостной хроматографии. Целью исследования был выбор исходных веществ и оптимальных условий синтеза. В результате исследования показано преимущество бромбензогидрола над хлорбензогидролом. Далее для бромбензогидрола найдены оптимальные условия по температуре и времени для получения наилучшей конверсии при ограничении вариативности состава.

 Некоторые результаты исследований представлены на рисунке 8.
Некоторые результаты исследований представлены на рисунке 8.
На графике (рис. 8б) видно, что конверсия выше в реакции, где участвует бромдифенилметан. В этом случае в полученной реакционной массе не остается примесей в качестве исходных реагентов, так как реагенты в процессе реакции расходуются полностью. Очевидно, что степень превращения в случае реакции с бромдифенилметаном равна 1, а селективность выше, чем в реакции с хлордифенилметаном. Поэтому далее проводились исследования для бромдифенилметана при постоянной температуре T =180 °C, варьируя время проведения реакции (нахождение реакционной смеси в капилляре) от 5 до 20 минут (рис. 8в). На рисун- ке 8г представлены зависимости степени превращения и селективности от состава исходной смеси.
Заключение
В статье рассмотрен системный подход к созданию алгоритмического и программного обеспечения для интеллектуальной системы управления разработкой синтеза АФИ на основе реализация принципа QbD. Показано преимущество схемы непрерывного синтеза про- изводства АФИ над схемой периодического синтеза.
Описана реализация системного подхода к формированию глобального критерия, и построены информационные модели для системы управления непрерывным синтезом АФИ димедрола в нотации IDEF0.
Разработано алгоритмическое и програм- мное обеспечение на основе свободно распространяемого программного комплекса Scilab для управления процессом разработки синтеза АФИ с помощью регрессионных многооткли- ковых моделей и алгоритма оптимизации Хука–Дживса.
Приведена графическая интерпретация некоторых результатов исследования процесса получения АФИ дифенгидрамина (димедрола) на уникальной микрореакторной установке Qmix непрерывного синтеза.
Показано преимущество исходного компонента бромбензогидрола над хлорбензогидролом. Для бромбензогидрола найдены оптимальные условия по температуре и времени для получения наилучшей конверсии при огра- ничении вариативности состава.
Литература
1. Решетников В.Н., Мамросенко К.А. Информационные технологии в здравоохранении: развитие региональных систем // Программные продукты, системы и алгоритмы. 2016. № 1. URL: http://swsys-web.ru/information-technology-in-health-caredevelopment-of-regional-systems.html (дата обращения: 10.09.2019).
2. Николаева О.М., Богунова И.В., Флид А.А., Гребенщиков А.А., Корнюшко В.Ф. Информационная поддержка стадии разработки состава твердых лекарственных форм // Программные продукты и системы. 2018. № 4. Т. 31. С. 814–822. DOI: 10.15827/0236-235X.124.814-822.
3. Жизненный цикл лекарственных средств; [под ред. Ю.В. Олефира, А.А. Свистунова]. М., 2018. 280 с.
4. Энде Д.Д. Производство лекарственных средств. Химическая технология от R&D до производства; [пер. с англ., под ред. В.В. Береговых]. СПб: Профессия, 2015. 1280 с.
5. Rubin E., Tummala S., Both D., Wang C., Delany E. Emerging technologics supporting chemical process R&D and their increasing impact on productivity in the pharmaceutical industry. Chem. Rev., 2006, vol. 106, no. 7, pp. 2794–2810.
6. Майофис Л.С. Технология химико-фармацевтических препаратов Л., 1968. 539 c.
7. Костров А.В., Головина Е.А., Корнюшко В.Ф., Кузин Р.Е. Подход к совершенствованию средств управления развитием персонала в автоматизированной системе предприятия // Информационные и телекоммуникационные технологии. 2015. № 28. С. 35–41.
8. Чуешов В.И., Гладух Е.В., Ляпунова О.А., Сайко И.В., Сичкарь А.А., Рубан Е.А., Крутских Т.В. Промышленная технология лекарств. 2010. URL: // http://ztl.nuph.edu.ua/html/medication/index.html (дата обращения: 10.09.2019).
9. Balogh A., Domokos A., Farkas B., Farkas A., Rapi Z., Kiss D., Nyiri Z., Eke Z., Szarka G., Örké- nyi R., Mátravölgyi B., Faigl F., Marosi G., Kristóf Nagy Z. Continuous end-to-end production of solid drug dosage forms: Coupling flow synthesis and formulation by electrospinning. Chem. Eng. J. 2018, vol. 350, no. 10, pp. 290–299. DOI: 10.1016/j.cej.2018.05.188.
10. Adamo A., Beingessner R.L., Behnam M., Chen J., Timothy F. etc. On-demand continuous-flow production of pharmaceuticals in a compact, reconfigurable system. Science. 2016, vol. 352, no. 61–67. DOI: 10.1126/science.aaf1337.
11. Корнюшко В.Ф., Панов А.В., Богунова И.В., Николаева О.М., Флид А.А. Применение системного подхода для построения информационного пространства разработки состава готовых лекарственных форм // Прикладная информатика. 2018. Т. 13. № 3. С. 83–100.
12. Меньшутина Н.В., Матасов А.В. Современные информационные системы хранения, обработки и анализа данных для предприятий химической и смежных отраслей. М.: Изд-во РХТУ, 2011. 308 с.
13. Мешалкин В.П. Экспертные системы в химической технологии. М.: Химия, 1995. 367 с.
14. Таптунов В.Н., Екимов С.Д., Гусева Е.В. Информационная интеллектуальная система для разработки схем производства твердых лекарственных форм // Программные продукты и системы. 2008. № 4. С. 160–161.
15. Андриевский А.Б., Андриевский Б.Р., Капитонов А.А., Фрадков А.Л. Решение инженерных задач в среде SciLab. СПб: Изд-во ИТМО, 2013. 97 с.
16. Hook R., Jeeves T.A. Direct search solution of numerical and statistical problems. JACM, 1961, vol. 8, iss. 2, pp. 212–229. DOI: 10.1145/321062.321069.
References
- Reshetnikov V.N., Mamrosenko K.A. Health service information technologies: developing regional systems. Software J.: Theory and Applications. 2016, no. 1. Available at: http://swsys-web.ru/en/information-technology-in-health-care-development-of-regional-systems.html (accessed September 10, 2019).
- Nikolaeva O.M., Bogunova I.V., Flid A.A., Grebenshchikov A.A., Kornyushko V.F Information support of the development stage of solid dosage form composition. Software & Systems. 2018, no. 4, vol. 31,
pp. 814–822. DOI: 10.15827/0236-235X.124.814-822 (in Russ.).
- Drug Life Cycle. Yu.V. Olefir, A.A. Svistunov (Eds). Mosсow, 2018, 280 p.
- Ende D.J. Chemical Engineering in the Pharmaceutical Industry. R&D to Manufacturing. John Wiley&Sons Publ., 2010 (Russ. ed.: St. Petersburg, Professiya Publ., 2015, 1280 p.).
- Rubin E., Tummala S., Both D., Wang C., Delany E. Emerging technologics supporting chemical process R&D and their increasing impact on productivity in the pharmaceutical industry. Chem. Rev. 2006, vol. 106,
no. 7, pp. 2794–2810.
- Mayofis L.S. Chemical Pharmaceutical Technology. Leningrad, 1968, 539 p.
- Kostrov A.V., Golovina E.A., Kornyushko V.F., Kuzin R.E. An approach to the improvement of personnel development management tools in a company automated system. Information and Telecommunication Technologies. 2015, no. 28, pp. 35–41 (in Russ.).
- Chueshov V.I., Gladukh E.V., Lyapunova O.A., Sayko I.V., Sichkar A.A., Ruban E.A., Krutskikh T.V. Industrial Drug Technology. 2010. Available at: http://ztl.nuph.edu.ua/html/medication/index.html (accessed September 10, 2019).
- Balogh A., Domokos A., Farkas B., Farkas A., Rapi Z., Kiss D., Nyiri Z., Eke Z., Szarka G., Örké-
nyi R., Mátravölgyi B., Faigl F., Marosi G., Kristóf Nagy Z. Continuous end-to-end production of solid drug dosage forms: Coupling flow synthesis and formulation by electrospinning. Chem. Eng. J. 2018, vol. 350,
no. 10, pp. 290–299. DOI: 10.1016/j.cej.2018.05.188.
- Adamo A., Beingessner R.L., Behnam M., Chen J., Timothy F. etc. On-demand continuous-flow production of pharmaceuticals in a compact, reconfigurable system. Science. 2016, vol. 352, no. 61–67. DOI: 10.1126/science.aaf1337.
- Kornyushko V.F., Panov A.V., Bogunova I.V., Nikolaeva O.M., Flid A.A. The application of the system approach for building the information space for the development of the production of ready medicines. Applied Informatics. 2018, vol. 13, no. 3, pp. 83–100 (in Russ.).
- Menshutina N.V., Matasov A.V. Modern Information Systems for Storing, Processing and Analyzing Data for Chemical and Related Industries. Moscow, 2011, 308 p. (in Russ.).
- Meshalkin V.P. Expert Systems in Chemical Technology. Moscow, Khimiya Publ., 1995, 367 p.
(in Russ.).
- Taptunov V.N., Ekimov S.D., Guseva E.V. An intelligent information system for developing a solid form process design. Software & Systems. 2008, no. 4, pp. 160–161 (in Russ.).
- Andrievsky A.B., Andrievsky B.R., Kapitonov A.A., Fradkov A.L. Solving Engineering Problems in Scilab. St. Petersburg, ITMO Univ. Publ., 2013, 97 p.
- Hook R., Jeeves T.A. Direct search solution of numerical and statistical problems. JACM. 1961, vol. 8, iss. 2, pp. 212–229. DOI: 10.1145/321062.321069.







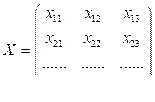 ;
; ;
; . (6)
. (6)

