Проектирование и разработка высокоточных радиоэлектронных систем, составной частью которых являются радиотехнические следящие системы (РТСС) различного целевого назначения (например, радиолокационные, радионавигационные, радиопеленгационные), размещаемые на различных носителях (стационарных, возимых, мобильных), – актуальная на сегодня проблема. В общем случае РТСС состоит из объекта управления (ОУ) (например, фазированной антенной решетки) и совокупности устройств (систем управления на основе автоматических регуляторов, следящих приводов и других подсистем), которые обеспечивают управление ОУ и являются для него управляющим устройством (УУ) [1].
Одно из направлений разработки таких систем – использование при синтезе УУ, состоящего, как правило, из оптимальных фильтра и регулятора, методов теорий стохастической фильтрации и оптимального управления [2]. Данные методы позволяют сформировать управление ОУ РТСС, оптимальное по минимуму интегрального функционала качества. Эффективность таких систем во многом зависит от степени соответствия реальных характеристик РТСС и условий их функционирования, таких как параметры отслеживаемого входного процесса, ОУ исполнительной части РТСС и внешних возмущений, действующих на ОУ системы (внешней среды), тем условиям и характеристикам, которые принимаются при их син- тезе. В реальных условиях функционирования РТСС данное соответствие, как правило, не соблюдается, а классические методы теории автоматического управления [1, 2], как и современные точные методы [3], могут работать неоптимально из-за параметрических и структурных неточностей в описании УУ и ОУ. Для решения этой проблемы необходимо применить адаптивный подход. Однако в случае его применения возникают сложности при идентификации параметров нестационарных моделей входных полезных сигналов, ОУ и внешней среды. Это особенно актуально при возможной скоротечности протекания процессов изменения данных параметров.
В связи с этим возникает необходимость проектирования и разработки адаптивных РТСС, функционирующих в условиях неопределенности, когда отсутствует точная информация о полезном входном сигнале, ОУ и внешней среде и данная информация изменяется в процессе функционирования РТСС, то есть при наличии неопределенности параметров обобщенного возмущения, действующего на систему.
Синтез адаптивных следящих систем в настоящее время хорошо проработан (например [4, 5]). Однако в большинстве публикаций в данной предметной области рассматривается синтез либо алгоритмов адаптивной фильтрации полезного сообщения [3], либо адаптивной системы управления (адаптивного регулятора) при наличии только неопределенности внешних возмущений, действующих на ОУ систе- мы [4, 6], или только неопределенности, вызванной изменением (нестационарностью) параметров ОУ исполнительной части системы в процессе ее функционирования [7, 8].
В реальных условиях функционирования РТСС возникают ситуации, когда неопределенными одновременно могут оказаться как параметры отслеживаемого входного процесса, так и ОУ РТСС и внешних возмущений, действующих на ОУ системы (обобщенное возмущение). На практике такие ситуации чаще всего возникают при размещении РТСС и их функционировании на мобильных носителях (наземных, воздушных и др.), когда определяющими являются нестационарность параметров входных полезных сигналов, скоротечность процессов, связанных с вибрационными, ветровыми, температурными, помеховыми и другими негативными воздействиями на ОУ. Поэтому возникает актуальная задача синтеза РТСС, функционирующей при наличии не- определенности параметров обобщенного возмущения.
Цель – разработать метод синтеза алгоритмов функционирования адаптивной РТСС при наличии неопределенности (нестационарности) параметров обобщенного возмущения.
Постановка задачи
Пусть РТСС с ОУ, описываемым дискретными уравнениями вида
z(i+1) = A(i)z(i) + B(i)u(i) + w(i), (1)
 = C(i)z(i),
= C(i)z(i),
предназначена для отслеживания входного полезного процесса (сообщения), например, координат объекта
a(i+1) = Ф(i)a(i) + Г(i)h(i), (2)
при наличии наблюдений (измерений) вида
y(i) = kд(i)[a(i) –  + n(i), (3)
+ n(i), (3)
где z(i) – n-мерный вектор состояния;  – n-мерный вектор выхода; A(i), B(i), C(i) – матрицы размером n´n; u(i) – n-мерный вектор управления; a(i) – n-мерный вектор полезного сообщения; y(i) – n-мерный вектор наблюдения (при синтезе полагается, что модель дискриминатора представлена в виде линеаризованного динамического эквивалента); Ф(i) – матрица состояния размером n´n; Г(i) – матрица при шумах возбуждения размером n´n; h(i) – n-мерный вектор шумов возбуждения, представляющий собой нормальный белый шум с нулевым математическим ожиданием (МО) и корреляционной матрицей (КМ) M{h(i)hT(j)} = = Dhdij, M{…} – оператор МО, Dh – симметрическая неотрицательно определенная матрица дисперсий шумов возбуждения; w(i) – n-мерный вектор возмущений, представляющий собой нормальный белый шум с нулевым МО и КМ M{w(i)wT(j)} = Dwdij, Dw – симметрическая неотрицательно определенная матрица дисперсий шумов возмущения; kд – матрица коэффициентов усиления дискриминатора размером n´n; n(i) – n-мерный вектор шумов измерения, представляющий собой нормальный белый шум с нулевым МО и КМ M{n(i)nT(j)} = Qdij, Q – симметрическая положительно определенная матрица дисперсий ошибок измерения.
– n-мерный вектор выхода; A(i), B(i), C(i) – матрицы размером n´n; u(i) – n-мерный вектор управления; a(i) – n-мерный вектор полезного сообщения; y(i) – n-мерный вектор наблюдения (при синтезе полагается, что модель дискриминатора представлена в виде линеаризованного динамического эквивалента); Ф(i) – матрица состояния размером n´n; Г(i) – матрица при шумах возбуждения размером n´n; h(i) – n-мерный вектор шумов возбуждения, представляющий собой нормальный белый шум с нулевым математическим ожиданием (МО) и корреляционной матрицей (КМ) M{h(i)hT(j)} = = Dhdij, M{…} – оператор МО, Dh – симметрическая неотрицательно определенная матрица дисперсий шумов возбуждения; w(i) – n-мерный вектор возмущений, представляющий собой нормальный белый шум с нулевым МО и КМ M{w(i)wT(j)} = Dwdij, Dw – симметрическая неотрицательно определенная матрица дисперсий шумов возмущения; kд – матрица коэффициентов усиления дискриминатора размером n´n; n(i) – n-мерный вектор шумов измерения, представляющий собой нормальный белый шум с нулевым МО и КМ M{n(i)nT(j)} = Qdij, Q – симметрическая положительно определенная матрица дисперсий ошибок измерения.
Необходимо найти соответствующее допустимое управление uопт.(i), определенное на интервале дискретизации [0, m] и зависящее от текущих значений отслеживаемого процесса, такое, чтобы показатель качества вида

 (4)
(4)
(R – симметрическая положительно определенная весовая матрица) принимал минимальное значение на множестве допустимых управлений U (u(i) Ì U) при условии, что некоторые элементы матриц Ф, Г, Dh, характеризующие отслеживаемый процесс, и некоторые элементы матриц A, B, Dw, характеризующие состояние ОУ РТСС, могут быть неизвестны, а область пространства возможных значений ошибки функционирования (рассогласования) РТСС da(i) = a(i) –  должна быть существенно меньше некоторой заданной величины, например, полуширины дискриминационной характеристики Δ (|da(i) | << Δ).
должна быть существенно меньше некоторой заданной величины, например, полуширины дискриминационной характеристики Δ (|da(i) | << Δ).
Так как рассматриваемая РТСС наблюдаема и управляема, при синтезе адаптивной РТСС будем использовать принцип разделения [5], согласно которому УУ РТСС должно состоять из адаптивного фильтра для оценки полезного сообщения при наличии неопределенности его параметров и адаптивной системы управления для управления ОУ РТСС при наличии неопределенности его параметров и внешних возмущений, действующих на него.
Известны несколько подходов к синтезу адаптивных фильтров [3–5]. Один из них состоит в том, что неизвестные параметры включаются в число оцениваемых и рассматривается задача фильтрации расширенного вектора состояния [3]. Существует подход к синтезу адаптивных фильтров на основе оценки неизвестных статистических характеристик сообщения и помех с использованием их для изменения параметров фильтра [5]. Данные подходы приводят к аналитическим усложнениям алгоритмов фильтрации и значительным вычислительным затратам. Еще один подход к синтезу адаптивных фильтров основан на том, что оценки неизвестных параметров формируются отдельным блоком адаптации и используются для корректировки параметров основного блока фильтрации [4]. Реализация его проще, чем в [3, 5], однако он также требует значительных вычислительных затрат, так как на каждом шаге адаптации необходимо пересчитывать матрицы дисперсий ошибок фильтрации и коэффициентов усиления фильтра. В статье предлагается обойти данную трудность за счет реа- лизации скользящего алгоритма адаптации на основе непосредственной оценки параметров фильтра, в частности, весовых коэффициентов усиления, формируемых блоком адаптации и используемых в основном фильтре [9, 10].
Для синтеза адаптивной системы управления при одновременном наличии неопределенности параметров ОУ РТСС и внешних возмущений, действующих на него, предлагается использовать двухуровневую структуру [2], включающую два этапа синтеза: основного контура управления (оптимального регулятора) и контура адаптации (адаптивного регулятора).
Оптимальный регулятор синтезируется на основе принципов теории оптимального управления стохастическими процессами по критерию минимума показателя (4) при условии, что параметры ОУ РТСС постоянны и известны, а внешние возмущения не меняются (либо отсутствуют) (эталонная модель РТСС) [6, 11].
Синтез адаптивного регулятора проводится для случая одновременного наличия неопределенности параметров ОУ РТСС и внешних возмущений, действующих на него, по критерию минимума ошибки функционирования модели возмущения РТСС на основе рекуррентной модификации метода идентификации по наименьшим квадратам [6].
Синтез адаптивного фильтра
Для синтеза адаптивного фильтра воспользуемся подходом из работы [9]. Если матрицы Ф, Г, Dh и Q полностью определены, то оптимальным по критерию минимума показателя (4) для оценивания сообщения (2) при наблюдении (3) является фильтр Калмана [12], описываемый соотношениями:

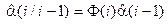 , (5)
, (5)

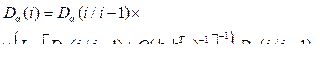

где  – оптимальная оценка отслеживаемого сообщения;
– оптимальная оценка отслеживаемого сообщения;  – экстраполированная оценка отслеживаемого сообщения; K(i) – матрица коэффициентов усиления фильтра.
– экстраполированная оценка отслеживаемого сообщения; K(i) – матрица коэффициентов усиления фильтра.
При неопределенности матриц Ф, Г, Dh оп- тимальную матрицу K(i) определить по (5) не- возможно, и в фильтре будет использоваться некоторая неоптимальная матрица коэффициентов усиления K*(i). Тогда оценки, формируемые данным фильтром, также будут неоптимальными:

 , (6)
, (6)
где Ф*(i) – аналог матрицы состояния Ф(i) в оптимальном фильтре, но с другими параметрами.
Поставим задачу отыскания такой матрицы коэффициентов усиления К*(i), при которой функционал (4) достигает своего минимума при неопределенности Ф, Г, Dh. Для этого воспользуемся методикой, предложенной в [13] и заключающейся в том, что оптимизация (4) рассматривается с точки зрения теории оптимального управления. В [9] показано, что (4) имеет минимум при тех значениях К*(i), которые минимизируют матрицу дисперсий ошибок экстраполяции сообщения Da(i/i – 1) из (5), зависящую от К*(i). При этом полагается, что Da(i/i – 1) является состоянием системы, а К*(i) – управлением, которое нужно оптимизировать на интервале функционирования системы [0, m] так, чтобы функционал (4) имел минимум, причем матрица К* рассматривается как функция вектора k(i) = [k11(i), …, knn(i)], компоненты которого kij(i) являются элементами данной матрицы.
Для нахождения оценки  , минимизирующей функционал (4), вводится вспомогательная функция:
, минимизирующей функционал (4), вводится вспомогательная функция:
 (7)
(7)
где l(i+1) – функционально сопряженные неопределенные множители Лагранжа [14].
Тогда канонические уравнения для К*(i+1) и l(i) можно записать в виде


с граничными условиями на концах [0, m] – К*(0) = k0, l(m) = 0 [14].
Используя подход, предложенный в [3], получаем следующие уравнения для матрицы оценок коэффициентов усиления фильтра  :
:
 (8)
(8)


где P(i+1) имеет смысл дисперсии ошибки оценки коэффициентов усиления фильтра.
Первая и вторая производные, входящие в (8), получаются путем дифференцирования (6) по К*(i). Тогда имеем:
 (9)
(9)

Объединив (6), (8) и (9), получаем уравнения адаптивного фильтра:
 ,
,


 (10)
(10)

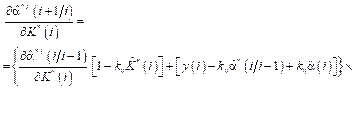

 Из (10) следует, что адаптивный фильтр состоит из двух блоков (рис. 1): основного блока фильтрации, описываемого первым и вторым соотношениями, и блока адаптации, описываемого третьим, четвертым, пятым и шестым соотношениями, формирующего оценки коэффициентов усиления
Из (10) следует, что адаптивный фильтр состоит из двух блоков (рис. 1): основного блока фильтрации, описываемого первым и вторым соотношениями, и блока адаптации, описываемого третьим, четвертым, пятым и шестым соотношениями, формирующего оценки коэффициентов усиления  , используемые в основном блоке фильтрации вместо значений K(i).
, используемые в основном блоке фильтрации вместо значений K(i).
Предложенный подход к синтезу адаптивного фильтра оправдан, если неизвестными являются Dh и Г(i), так как только они влияют на K(i). В случае неопределенности Ф(i) использованием  в фильтре можно только частично компенсировать ее неопределенность, так как она определяет не только K(i), но и Ф*(i) в фильтре. Поскольку в реальных условиях функционирования РТСС формирование Ф(i) осуществляется на основе некоторой известной статистической информации, этого достаточно для получения эффективной оценки полезного сообщения, формируемого данным фильтром.
в фильтре можно только частично компенсировать ее неопределенность, так как она определяет не только K(i), но и Ф*(i) в фильтре. Поскольку в реальных условиях функционирования РТСС формирование Ф(i) осуществляется на основе некоторой известной статистической информации, этого достаточно для получения эффективной оценки полезного сообщения, формируемого данным фильтром.
Синтез адаптивной системы управления
Для синтеза адаптивной системы управления воспользуемся идентификационным подходом [5], позволяющим в условиях неопределенности параметров ОУ РТСС и внешних возмущений получать оценки возмущений, действующих на ОУ РТСС, и использовать их для формирования управления, компенсирующего данные неопределенности [13].
Представим эталонную модель функционирования ОУ РТСС в виде разностного уравнения:
zM(i) = AM(i)zM(i) + BM(i)uM(i),
 , (11)
, (11)
где матрицы AM(i), BM(i), C(i) и векторы zM(i), uM(i),  имеют смысл и размерность, аналогичные в (1) матрицам A(i), B(i), C(i) и векторам z(i), u(i),
имеют смысл и размерность, аналогичные в (1) матрицам A(i), B(i), C(i) и векторам z(i), u(i),  . При этом в соответствии с подходом [5] будем полагать, что матрицы AM(i) = A(i) – F(i) и BM(i) = B(i) – G(i), а векторы zM(i) = z(i) – dz(i) и uM(i) = u(i) – du(i), где F(i), G(i) – матрицы возмущений размером n´n; dz(i), du(i) – n-мерные векторы возмущения векторов состояния и управления соответственно.
. При этом в соответствии с подходом [5] будем полагать, что матрицы AM(i) = A(i) – F(i) и BM(i) = B(i) – G(i), а векторы zM(i) = z(i) – dz(i) и uM(i) = u(i) – du(i), где F(i), G(i) – матрицы возмущений размером n´n; dz(i), du(i) – n-мерные векторы возмущения векторов состояния и управления соответственно.
Вычитая из первого и второго соотношений (1) соответственно первое и второе соотношения (11), получаем модель возмущения ОУ РТСС:
dz(i+1) = F(i) dz(i) + G(i) du(i) + w(i), (12)
de(i) =  (13)
(13)
Синтез адаптивной системы управления сводится к определению управления du(i), компенсирующего возмущение de(i), которое может быть получено, например, на основе одношагового закона оптимального управления [11] в предположении, что скорость изменения параметров ОУ исполнительной части РТСС меньше скорости адаптации; переменные de(i) поддаются измерению, а погрешность их измерения мала.
Нахождение управления du(i) требует, чтобы матрицы F(i) и G(i) были известны в каждый момент времени управления. Воспользуемся идентификационным подходом [5]. Для этого, записывая i-ю строку неизвестных параметров в (12) в виде вектора
 (14)
(14)
i = 1, …, n,
и представляя выходы и входы в (12) вектором xT(i) = [dz1(i), …, dzn(i), du1(i), …, dun(i)], а состояние системы вектором dzT(i) = [dz1(i), …, dzn(i)], трансформируем (12) к виду
dzi(i+1) = xT(i)qi(i) + wi(i), i = 1, …, n. (15)
Минимизируя ошибки функционирования модели возмущения ОУ РТСС (15) относительно вектора qi(i) по критерию предсказания вида
 (16)
(16)
на основе метода идентификации по наименьшим квадратам [6] получаем следующие соотношения для его оценки:
 ,
,
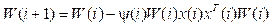 , (17)
, (17)
 ,
,
W(0) = mI, m >> 1,  .
.
После определения по (17) оценок матриц  может быть сформирован закон оптимального управления ОУ РТСС с учетом возмущающих факторов, удовлетворяющий требованиям уравнений (1), (12) и минимизирующий показатель качества (4). Используя уравнение, описывающее отслеживаемый процесс (2), и уравнение функционирования ОУ РТСС (11), введем расширенные уравнения состояния и ошибки слежения:
может быть сформирован закон оптимального управления ОУ РТСС с учетом возмущающих факторов, удовлетворяющий требованиям уравнений (1), (12) и минимизирующий показатель качества (4). Используя уравнение, описывающее отслеживаемый процесс (2), и уравнение функционирования ОУ РТСС (11), введем расширенные уравнения состояния и ошибки слежения:
 ,
,
 ,
,
где 
 .
.
Применяя принципы теории оптимального управления стохастическими процессами [5, 11], можно получить управление ОУ РТСС uопт.(i), минимизирующее показатель качества (4) с учетом обобщенного возмущения и удовлетворяющее требованиям соотношений (1) и (12):


 (18)
(18)
где ; S(m) = Q–1;
; S(m) = Q–1;  – матрица передачи оптимального регулятора; d
– матрица передачи оптимального регулятора; d – матрица передачи адаптивного регулятора; u*(i) – оптимальное управление при отсутствии возмущений; du*(i) – оптимальное управление, минимизирующее ошибки слежения системы по возмущениям de(i);
– матрица передачи адаптивного регулятора; u*(i) – оптимальное управление при отсутствии возмущений; du*(i) – оптимальное управление, минимизирующее ошибки слежения системы по возмущениям de(i); 
Из (18) следует, что адаптивная система управления ОУ РТСС при обобщенном возмущении включает двухуровневую структуру: оптимальный регулятор при отсутствии возмущений (первое слагаемое в (18)) и адаптивный регулятор при наличии возмущений (второе слагаемое в (18)).
Блок-схема синтезированной адаптивной РТСС приведена на рисунке 1.
Пример
Для оценки эффективности разработанного метода воспользуемся подходами, предложенными в [9, 10]. В качестве показателя эффективности функционирования адаптивной РТСС принимается выигрыш в точности адаптации b [10], который достигается использованием адаптивной РТСС вместо неадаптивной, синтезированной при известных характеристиках отслеживаемого процесса, ОУ РТСС и внешних возмущений, действующих на ОУ системы. Оценить его можно отношением дисперсий ошибок слежения в неадаптивной  и адаптивной
и адаптивной  РТСС вида
РТСС вида
 , (19)
, (19)
где  ,
,
 ,
,
 .
.
 Выигрыш в точности адаптации b рассчитывался по соотношению (19) для случаев наличия параметрической и структурной неопределенностей характеристик отслеживаемого сообщения (2) с учетом соотношений (10), (17), (18). При параметрической неопределенности полагалось, что
Выигрыш в точности адаптации b рассчитывался по соотношению (19) для случаев наличия параметрической и структурной неопределенностей характеристик отслеживаемого сообщения (2) с учетом соотношений (10), (17), (18). При параметрической неопределенности полагалось, что  (в матрице состояния параметр g отличается от его значения g*, принятого при синтезе системы, только величиной), а при структурной –
(в матрице состояния параметр g отличается от его значения g*, принятого при синтезе системы, только величиной), а при структурной – 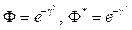 (параметр g отличается и структурой, и величиной от его значения g*, принятого при синтезе системы). Результаты расчетов получены для установившегося режима фракционирования РТСС, задаваемого условием Dd(i) – Dd(i – 1) = 0,01, при следующих исходных данных: A = B = Г = C = kд = 1, Dw = 0,1, Q = 0,25, R = 0,1, Dh = 0,5, m = 10. Семейство зависимостей выигрыша в точности адаптации b = f(g), рассчитаное при нескольких фиксированных (эталонных) значениях параметра gmax = g* (0,01; 1; 100) для параметрической (сплошные линии) и структурной (штриховые линии) неопределенностей характеристик отслеживаемого сообщения приведены на рисунке 2. Зависимости рассчитывались для отклонения параметра g от его фиксированного значения g* = gmax. Видно, что выигрыш в точности адаптации b зависит от того, насколько параметры реального отслеживаемого процесса отличаются от значений параметров, принятых при синтезе системы. Если g = gmax, то b = 1 и выигрыша нет. По мере увеличения отклонения Dg = gmax – g увеличивается выигрыш в точности адаптации b, причем b при структурной неопределенности выше, чем при параметрической. Поэтому структурная неопределенность оказывает на точность функционирования РТСС более сильное негативное влияние, чем параметрическая. Вместе с тем анализ зависимостей, приведенных на рисунке 2, показывает, что введение адаптации в РТСС на основе разаботанного метода позво- ляет существенно снизить влияние неопределенностей характеристик отслеживаемого сообщения на эффективность функционирования РТСС, в частности, практически полностью устранить влияние параметрической неопределенности дисперсии аддитивного шума измерений на работу РТСС при отклонении значения рассматриваемого (отслеживаемого) параметра g от его фиксированного значения g* на 25–35 %. Кроме того, исследование частных задач фильтрации параметров сообщения следящей системой, приведенное в [10], показало, что отказ от нормировки на матрицу дисперсий аддитивного шума измеренй Q в разработанных в статье соотношениях приводит лишь к некоторому ухудшению процесса адаптации, заключающемуся в его затягивании по времени.
(параметр g отличается и структурой, и величиной от его значения g*, принятого при синтезе системы). Результаты расчетов получены для установившегося режима фракционирования РТСС, задаваемого условием Dd(i) – Dd(i – 1) = 0,01, при следующих исходных данных: A = B = Г = C = kд = 1, Dw = 0,1, Q = 0,25, R = 0,1, Dh = 0,5, m = 10. Семейство зависимостей выигрыша в точности адаптации b = f(g), рассчитаное при нескольких фиксированных (эталонных) значениях параметра gmax = g* (0,01; 1; 100) для параметрической (сплошные линии) и структурной (штриховые линии) неопределенностей характеристик отслеживаемого сообщения приведены на рисунке 2. Зависимости рассчитывались для отклонения параметра g от его фиксированного значения g* = gmax. Видно, что выигрыш в точности адаптации b зависит от того, насколько параметры реального отслеживаемого процесса отличаются от значений параметров, принятых при синтезе системы. Если g = gmax, то b = 1 и выигрыша нет. По мере увеличения отклонения Dg = gmax – g увеличивается выигрыш в точности адаптации b, причем b при структурной неопределенности выше, чем при параметрической. Поэтому структурная неопределенность оказывает на точность функционирования РТСС более сильное негативное влияние, чем параметрическая. Вместе с тем анализ зависимостей, приведенных на рисунке 2, показывает, что введение адаптации в РТСС на основе разаботанного метода позво- ляет существенно снизить влияние неопределенностей характеристик отслеживаемого сообщения на эффективность функционирования РТСС, в частности, практически полностью устранить влияние параметрической неопределенности дисперсии аддитивного шума измерений на работу РТСС при отклонении значения рассматриваемого (отслеживаемого) параметра g от его фиксированного значения g* на 25–35 %. Кроме того, исследование частных задач фильтрации параметров сообщения следящей системой, приведенное в [10], показало, что отказ от нормировки на матрицу дисперсий аддитивного шума измеренй Q в разработанных в статье соотношениях приводит лишь к некоторому ухудшению процесса адаптации, заключающемуся в его затягивании по времени.
Исследования показали, что использование предлагаемого метода и реализующих его алгоритмов при функционировании высокоточных радиолокационных систем на основе фазированных антенных решеток позволяет повысить точность оценки (экстраполяции) параметров траектории движения летательных аппаратов (например, их координат), описываемой полиномом третьей степени, по сравнению с оцениванием на основе стандартных алгоритмов калмановской фильтрации [15, 16] при наличии неопределенности (отклонения) параметров отслеживаемого процесса от предполагаемых (эталонных, принятых при синтезе системы) и ограниченной выборке измерений данных параметров в среднем на 15–25 % [17], что, как следствие, приводит к повышению точности сопровождения данных объектов радиолокационными системами при недостаточной априорной информации о полезном входном сигнале и параметрах фазированной антенной решетки системы.
Выводы
В статье предложен подход к синтезу управляющего устройства адаптивной РТСС, включающий в себя синтез алгоритма адаптивной фильтрации и алгоритма адаптивного управления по обобщенному возмущению. Синтез адаптивного фильтра проведен на основе метода адаптивной фильтрации, предполагающего непосредственную регулировку коэффициентов усиления фильтра, а синтез алгоритма адаптивного управления – на основе параметрической идентификации по методу наименьших квадратов и методов теории оптимального стохастического управления. Предложенный подход позволил формализовать задачу функционирования адаптивной РТСС в условиях неопределенности параметров отслеживаемого процесса, состояния ОУ исполнительной части РТСС и внешних возмущений, действующих на ОУ данной системы (обобщенного возмущения). Получены новые соотношения для оценок коэффициентов усиления адаптивного фильтра и матрицы передачи адаптивного регулятора при наличии возмущений ОУ.
Разработанная на основе предлагаемого метода адаптивная РТСС обеспечивает эффек- тивное функционирование в рамках формализованного описания качества на основе показателя, определенного квадратичным функционалом, который характеризует точность работы системы и затраты на ее управление, что подтверждается приведенными в статье результатами оценки эффективности функционирования синтезированной адаптивной РТСС в условиях воздействия на нее обобщенного возмущения.
Практическая реализация алгоритмов функционирования РТСС, реализующих разработанный метод, позволит повысить эффективность функционирования РТСС различного целевого назначения, в частности, радиолокационных систем на основе фазированных антенных решеток, размещаемых на мобильных носителях (наземных, воздушных и др.), когда определяющими негативными факторами, влияющими на их работу, являются нестационарность входных полезных сигналов, скоротечность процессов, связанных с негативными воздействиями на систему внешней среды, например, при сопровождении траекторий движения летательных аппаратов в условиях наличия неопределенности параметров отслеживаемых координат, вибрационных и помеховых воздействий на систему.
Предлагаемый подход также может быть использован при разработке оптико-электронных локационных систем, требующих получения и обеспечения более высокой точности функционирования по сравнению с радиотехническими системами.
Литература
1. Репин В.Г., Тартаковский Г.П. Статистический синтез при априорной неопределенности и адаптации информационных систем. М.: Сов. радио, 1977. 432 с.
2. Сейдж Э.П., Мелс Дж. Идентификация систем управления. М.: Наука, 1974. 246 с.
3. Первачев С.В., Перов А.И. Адаптивная фильтрация сообщений. М.: Радио и связь, 1991. 160 с.
4. Фрадков А.Л. Адаптивное управление в сложных системах. М.: Наука, 1990. 296 с.
5. Красовский А.А. Справочник по теории автоматического управления. М.: Наука, 1987. 712 с.
6. Цыпкин Л.З. Адаптивно инвариантные дискретные системы управления // Автоматика и телемеханика. 1991. № 5. С. 96–124.
7. Куржанский А.Б. Управление и наблюдение в условиях неопределенности. М.: Наука, 1977. 392 с.
8. Ци Э., Бар-Шолом Я. Активно адаптивное управление нелинейными стохастическими системами // ТИИЭР. 1976. № 8. С. 52–61.
9. Буцев С.В. К вопросу оценки чувствительности следящих систем к неопределенностям характеристик отслеживаемого процесса // Автоматика и телемеханика. 1992. № 8. С. 25–31.
10. Буцев С.В., Зайцев А.Г., Тикменов В.Н. Оценка чувствительности адаптивных следящих систем к неопределенностям характеристик входных сигналов // Радиотехника. 2004. № 5. С. 29–34.
11. Егоров А.И. Основы теории управления. М.: Физматлит, 2004. 504 с.
12. Синицын И.Н. Фильтры Калмана и Пугачева. М.: Логос, 2007. 772 с.
13. Буцев С.В. Алгоритмы функционирования адаптивной оптической системы фазового сопряжения // Квантовая электроника. 1996. Т. 23. № 8. С. 753–758.
14. Перов А.И. Статистическая теория радиотехнических систем. М.: Радиотехника, 2003. 400 с.
15. Мазурова М.А. Выбор коэффициентов диффузии для фильтра Калмана с компенсацией скоростной ошибки по дальности // Радиотехника. 2019. № 10. С. 32–42. DOI: 10.18127/j00338486-201910(15)-06.
16. Перов А.И. Синтез и анализ оптимального алгоритма контроля слежения по задержке в навигационном приемнике // Радиотехника. 2019. № 9. С. 5–13. DOI: 10.18127/j00338486-201909(14)-01.
17. Буцев С.В., Горюнов Г.А., Прохоров В.А., Сердешнов Е.А., Шепеть И.П. Повышение качества оценки параметров траектории движения летательного аппарата // Радиотехника. 2001. № 5. С. 96–100.
References
- Repin V.G., Tartakovsky G.P. Statistical Synthesis with a Priori Uncertainty and Adaptation of Information Systems. Moscow, 1977, 432 p. (in Russ.).
- Sage A.P., Melsa J.L. System Identification. Moscow, 1974, 246 p. (in Russ.).
- Pervachev S.V., Perov A.I. Adaptive Message Filtration. Moscow, 1991, 160 p. (in Russ.).
- Fradkov A.L. Adaptive Control in Complex Systems. Moscow, 1990, 296 p. (in Russ.).
- Krasovskiy A.A. Automatic Control Theory Reference Guide. Moscow, 1987, 712 p. (in Russ.).
- Tsypkin L.Z. Adaptively invariant discrete control system. Automation and Remote Control, 1991,
no. 5, pp. 96–124 (in Russ.).
- Kurzhansky A.B. Control and Observation in the Condition of Indeterminacy. Moscow, 1977, 394 p. (in Russ.).
- Tsi E., Bar-Sholom Ya. Actively adaptive control of nonlinear stochastic systems. Proc. IEEE, 1976, no. 8, pp. 52–61 (in Russ.).
- Butsev S.V. On an estimate for the sensitivity of tracking systems to uncertainties in the characteristics of the tracked process. Automation and Remote Control, 1992, no. 8, pp. 25–31 (in Russ.).
- Butsev S.V., Zaytsev A.G., Tikmenov V.N. Evaluation of the adaptive servo systems sensitivity to uncertainties in input signal characteristics. Radiotekhnika, 2004, no. 5, pp. 29–34 (in Russ.).
- Egorov А.I. Fundamentals of Management Theory. Moscow, 2004, 504 p.
- Sinitsyn I.N. Kalman and Pugachev Filters. Moscow, 2007, 772 p. (in Russ.).
- Butsev S.V. Algorithms for the operation of an adaptive optical phase conjugation system. Quantum Electronics, 1996, vol. 23, no. 8, pp. 753–758 (in Russ.).
- Perov A.I. Statistic Theory of Radio Engineering Systems. Moscow, 2003, 400 p. (in Russ.).
- Мазурова М.А. Kalman filter with range-Doppler coupling compensation: choice of diffusion coefficients. Radiotekhnika, 2019, no. 10, pp. 32–42 (in Russ.). DOI: 10.18127/j00338486-201910(15)-06.
- Perov A.I. Synthesis and analysis an optimal code delay lock detector algorithm in a satellite navigation receiver. Radiotekhnika, 2019, no. 9, pp. 5–13 (in Russ.). DOI: 10.18127/j00338486-201909(14)-01.
- Butsev S.V., Goryunov G.A., Prokhorov V.A., Serdeshnov E.A., Shepet I.P. Improving the quality of estimating the parameters of the motion trajectory of the aircraft. Radiotekhnika, 2001, no. 5, pp. 96–100 (in Russ.).
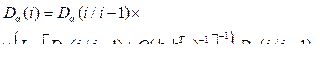
 (7)
(7)
 (8)
(8)

 (9)
(9)


 (10)
(10)