Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: V.B. Tarasov (vbulbov@yahoo.com) - Bauman Moscow State Technical University (Associate Professor), Moscow, Russia, Ph.D, () - | |
| Ключевое слово: |
|
| Page views: 11070 |
Print version Full issue in PDF (1.41Mb) |
С развитием теории агентов все большую роль в искусственном интеллекте (ИИ) начинает играть моделирование различных интенциональных характеристик, в частности, желаний, намерений, обязательств и мнений. Проблема исследования категории мнения (belief) имеет давние и глубокие традиции. Еще Платон ясно осознавал наличие промежуточных градаций, ступеней формирования знания. Он различал собственно знание и мнение: «мнение не есть знание, но и не есть незнание: оно темнее знания и светлее незнания» [1]. Знаниями в классическом ИИ называются «обоснованные, истинные убеждения» (мнения) [2,3]. Для того чтобы суждение или умозаключение стало знанием, оно должно пройти проверку на полноту и непротиворечивость. Однако реальные человеческие высказывания, оценки или рассуждения «здравого смысла» редко удовлетворяют этим жестким требованиям, определяющим статус знаний в ИИ. Здесь речь идет, скорее, о мнениях (точках зрения), которые отражают локальные представления о мире, пронизанные НЕ-факторами [4]. Мнения носят не достоверный, а правдоподобный характер, зависят от ситуации и нередко могут пересматриваться. Таким образом, мнение автономного агента, которое может описывать состояния мира, других агентов и самого агента, всегда является частичным, неточным, неоднозначным, а подчас и противоречивым [5]. Это означает, что в основу представления мнений следует положить аппарат многозначных логик [6,7]. В настоящей статье вводится интегральная модель мнений агента, включающая истинностные и модальные суждения и оценки, предлагается метод двухкоординатного представления систем модальностей и их формализации с помощью решеток и биупорядоченных множеств, строятся основные операции над модальными значениями. Описания и предписания в деятельности агента Функционирование любого агента опирается как на описания, так и на предписания. И описания, и предписания отражают информационные отношения между агентом и его средой: в первом случае – это информация о состояниях среды, воспринимаемых агентом, а во втором – о возможных действиях агента на эту среду. С одной стороны, представления агента о мире выражаются в виде истинностных суждений описательного характера, то есть высказываний вида p = X есть А, характеризуемых значениями истинности vÎ V. Истинностные суждения могут применяться и при формализации действий агента. Так, согласно [8], императивными аналогами истины и лжи являются понятия выполнения и невыполнения. Действие выполняется (не выполняется) тогда и только тогда, когда описывающее его содержание предложение становится истинным (ложным). С другой стороны, различные запросы, предписания, требования пользователя или других агентов выступают как внешние источники целеобразования и регуляторы поведения агента. Таким образом, при формализации агента следует использовать как доксастические модальности (модальности мнения), так и деонтические модальности (модальности действий и норм). К числу модальностей мнения относятся: «уверен», «предполагаю», «сомневаюсь», «отвергаю». В частности, исходное мнение агента может выступать в форме предположения (гипотезы) – предварительного (возможного) представления агента о мире и других агентах, которое может выдвигаться в интересах запуска механизма действия, направленного на его подтверждение, то есть на формирование уверенности. Примерами деонтических модальностей являются слова «обязательно», «разрешено», «запрещено», а также «может» и «должен». У агентов прагматические суждения оценочного характера опираются на стандарты, образцы, эталоны и т.п. При этом образец принципиально отличается от примера. Пример говорит о том, что имеет место в действительности, а образец – о том, что должно быть. Примеры используются для поддержки описательных высказываний, а ссылки на образцы служат обоснованием предписаний и требований. Легко понять, что в теории агентов центральное место занимает именно формализация предписаний, оценок, норм. Реализация агентом нормативного поведения предполагает наличие, по крайней мере, двух элементов: нормы, обязательной для выполнения в данной ситуации, и оценки степени выполнения ее предписаний. Нормы – это социальные запреты и ограничения, накладываемые сообществом (организацией) на отдельного агента. Нормы представляют собой частный случай оценок: их можно рассматривать как общественно апробированные и закрепленные оценки. Средством, превращающим оценку в норму, является угроза наказания, то есть стандартизация норм осуществляется с помощью санкций. Еще К. Менгер установил прямую связь между предписанием šp («обязательно p») и «если не p, то наказание или ухудшение» [9]. Следует отметить, что классическая интерпретация истинности как соответствия высказывания действительности, введенная еще Аристотелем и развитая А. Тарским, далеко не всегда применима при описании интенций агента. В случае представления мнений и оценок агента могут использоваться также теория полезности (утверждающая, что истинность есть прагматическая оценка полезности или пригодности) и теория согласованности (когерентности), согласно которой высказывание агента считается истинным, если оно согласуется с остальной частью его знания. В самом деле, выдвижение агентом некоторых предположений требует проверки их практической полезности, а их оценка может быть связана с анализом согласованности этих предположений с имеющимися знаниями [10]. Помимо этого, современные концепции истинности могут опираться на идеи модализации истинности, предложенные А. Прайором и Н. Решером, а также на теорию Демпстера-Шейфера (и ее частный случай – теорию возможности [11]). Единый подход к представлению истинностных значений и модальностей на основе четырехзначной семантики Координация представлений и действий агента в различных ситуациях требует развития единого подхода к формализации описаний и предписаний. Опишем вариант такого единого подхода на базе четырехзначной логической семантики Данна-Белнапа [7,12] и ее обобщения с помощью биупорядоченных множеств. Предположим, что множество высказываний S состоит из множества истинностных суждений Sv и множества суждений с модальностями Sm: S=Sv È Sm. Будем представлять истинностное суждение в виде пары: sv= áp, v(p)ñ, svÎ Sv, где v(p) – функция мультиоценки (в смысле Дж. Данна) истинности высказывания pÎ P, v:P®V4, V4={T,F,B N}. Здесь T – «истина»; F – «ложь»; B – «истина и ложь одновременно» (противоречие); N – «ни истина и ни ложь» (полная неопределенность).
Таблицы истинности для конъюнкции и дизъюнкции Белнапа задаются следующим образом:
Рассмотрим аналогичный вариант описания различных классов модальностей с единых позиций. Возьмем в качестве двух базовых характеристик любой модальности ее «знак» и «силу». По аналогии с V4, имеем в простейшем случае четырехзначное множество модальностей М4={L, U, W, Y}, где L – сильная положительная модальность; U – слабая положительная модальность, W – слабая отрицательная модальность, Y – сильная отрицательная модальность. Таким образом, любое модальное суждение можно также представить в виде пары: sm=áp, m(p)ñ, smÎ Sm, где m(p) – функция модальной мультиоценки высказывания pÎ P, m:P®M4, M4 ={L, U, W, Y}. Тогда норму как предписание к действию можно выразить четверкой NR=áAG, act, M4, Wñ, где АG – множество агентов, которым адресована норма; actÎACT – действие, являющееся объектом нормативной регуляции (содержание нормы), W – множество миров, в которых применима норма (условия приложения, обстоятельства, в которых должно или не должно выполняться действие); М4={L,U,W,Y} – множество базовых модальностей, связанных с действием act: здесь L – «обязательно»; U – «разрешено»; W – «необязательно»; Y– «запрещено».
Логика ML4: основные положения и операции Вернемся к представлению модальностей на координатной плоскости. На оси абсцисс обозначим единицей модальность положительного знака, а нулем – модальность отрицательного знака. Аналогично по оси ординат обозначим единицей сильную модальность, а нулем – слабую. Перейдем к соответствующему двухкоординатному описанию модальностей в единичном квадрате (рис. 4): L=(1,1), U=(1,0), Y=(0,1), W=(0,0). Такая интерпретация позволяет развивать общий подход к описанию модальностей различных классов в теории агентов (см. табл.). Таблица Примеры модальностей, рассматриваемых в теории агентов
Модальные характеристики разных классов имеют общие формальные свойства. Независимо от того, к какой группе относятся модальности, они определяются друг через друга по одной и той же схеме. В частности, ùL=W (отрицание сильной положительной модальности есть слабая отрицательная модальность), ùW=L (отрицание слабой отрицательной модальности есть сильная положительная модальность), ùU=Y (отрицание слабой положительной модальности есть сильная отрицательная модальность), ùY=U (отрицание сильной отрицательной модальности есть слабая положительная модальность. Характерными примерами интерпретации этих модальностей являются связи между слабой нормой и сильной антинормой («то, что не разрешено, запрещено») и наоборот («то, что не запрещено, разрешено»).
Зададим на произвольном непустом конечном множестве модальностей M два различных отношения порядка £l и £u следующим образом: "p, qÎ P, p=(x1,y1), q=(x2,y2), p£lqÛx1£x2 и y1£y2; "p, qÎ P, p=(x1,y1), q=(x2,y2), p£uqÛx1£x2 и y1³y2. Интерпретации этих двух порядков могут быть различными, например, порядок сильной нормы и порядок слабой нормы, порядок необходимости (определенности) и порядок возможности, порядок уверенности и порядок предположения и пр. В частности, для М4 имеем W£lY£lL, W£lU£lL и Y£uW£uU, Y£uL£uU. Математическая структура áM, £ l ,£uñ является биупорядоченным множеством, поскольку здесь M есть непустое множество, а £l и £u – два различных отношения порядка. В том случае, когда упорядоченные множества áM, £l ñ и áM, £uñ образуют полные решетки, получаем предбирешетку. Двум различным отношениям порядка соответствуют различные пары решеточных операций Ä, Å и Ù и Ú.
Следует отметить, что структура áM, £l , £uñ не образует бирешетку, поскольку определенная естественным образом операция отрицания инвертирует оба порядка £l , £u:
По аналогии с логикой Белнапа L4, введем четырехзначную базовую логику модальных значений ML4 c помощью следующей псевдологической матрицы LMML4 =áМ4, ù, Ä, Å, Ù, Ú}, {L}ñ, где М4={L,U,W,Y} – множество логических значений (значений модальностей); {L} – выделенное логическое значение, а операции над логическими значениями определены выше. Предложенный в настоящей статье логико-алгебраический аппарат нашел применение при создании распределенной системы контроля доступа и оперативного управления безопасностью, построенной по принципам децентрализованного ИИ [5]. В частности, интегральная модель мнений агентов, включающая истинностные и модальные суждения и оценки, а также модель разрешения конфликтов между агентами на основе четырехзначных семантик были реализованы в интегрированной системе контроля платного доступа и учета автотранспорта sPARK, которая внедрена на более чем 40 объектах в России и СНГ. Список литературы 1. Платон. Сочинения. В 3-х томах/ Под ред. В.Ф. Асмуса и А.Ф. Лосева. – М., 1968. - Т.1. 2. Кандрашина Е.Ю., Литвинцева Л.В., Поспелов Д.А. Представление знаний о пространстве и времени в системах искусственного интеллекта. – М.: Наука, 1988. 3. Вагин В.Н., Головина Е.Ю., Загорянская А.А., Фомина М.В. Достоверный и правдоподобный вывод в интеллектуальных системах. – М.: Физматлит, 2004. 4. Нариньяни А.С. НЕ-факторы и инженерия знания: от наивной формализации к естественной прагматике. // Сб. тр. национ. конф. по ИИ: КИИ-94 (Рыбинск, сентябрь, 1994 г.). В 2-х т. Т.1 – Тверь: АИИ, 1994. – С.9-18. 5. Тарасов В.Б. От многоагентных систем к интеллектуальным организациям.– М. Эдиториал УРСС, 2002. 6. Зиновьев А.А. Очерки комплексной логики. – М.: Эдиториал УРСС, 2000. 7. Карпенко А.С. Многозначные логики. – М.: Наука, 1997. 8. Вригт фон Г.Х. Логико-философские исследования. Избранные труды: / Пер. с англ.– М.: Прогресс, 1986. 9. Ивин А.А. Основы теории аргументации. – М.: ВЛАДОС, 1997. 10. Финн В.К. Об интеллектуальном анализе данных// Новости искусственного интеллекта. –2004. – №3. – С. 3-18. 11. Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике: / Пер. с франц. – М.: Радио и связь, 1990. 12. Белнап Н., Стил Т. Логика вопросов и ответов / Пер. с англ. – М.: Прогресс 1981. 13. Ginsberg M. Multivalued Logics: a Unified Approach to Reasoning in AI// Computer Intelligence. – 1988. – Vol.4. – P.256-316. 14. Fitting M. Bilattices and the Theory of Truth// Journal of Philosophical Logic. – 1989. – Vol.19. – P.225-256. |
| Permanent link: http://swsys.ru/index.php?id=509&lang=en&page=article |
Print version Full issue in PDF (1.41Mb) |
| The article was published in issue no. № 2, 2006 |
Perhaps, you might be interested in the following articles of similar topics:
- Формулировка задачи планирования линейных и циклических участков кода
- Автоматизированная информационная система маркетолога
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
- Алгоритмы и программное обеспечение системы обработки топопланов
- О выборе числа процессоров в многопроцессорной вычислительной системе
Back to the list of articles
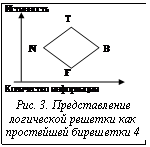

 Согласно Н. Белнапу, четыре истинностных значения из V4 образуют логическую решетку L4 (рис. 1) или аппроксимационную решетку А4 (получаемую в результате поворота логической решетки на 90°, рис. 2). В то же время, определив на множестве V4 два различных отношения порядка (порядок истинности £t и порядок информативности £i) вместе с условием связи между ними в виде унарной операции Ø, такой что: 1) если p£tq, то Øp³tØq; 2) если p£iq, то Øp£i Øq; 3) ØØp=p, "p, qÎ P, получаем представление четырехзначной семантики в виде простейшей бирешетки 22=4 [13,14] (рис. 3). Ее представимость в виде двойной диаграммы Хассе вытекает из выполнения условий F£tB£tT, F£tN£tT и N£iT£iB, N£iF£iB. Отметим, что в случае бирешетки 4 условие связи между порядками £t и £ i выражается через отрицание Белнапа:
Согласно Н. Белнапу, четыре истинностных значения из V4 образуют логическую решетку L4 (рис. 1) или аппроксимационную решетку А4 (получаемую в результате поворота логической решетки на 90°, рис. 2). В то же время, определив на множестве V4 два различных отношения порядка (порядок истинности £t и порядок информативности £i) вместе с условием связи между ними в виде унарной операции Ø, такой что: 1) если p£tq, то Øp³tØq; 2) если p£iq, то Øp£i Øq; 3) ØØp=p, "p, qÎ P, получаем представление четырехзначной семантики в виде простейшей бирешетки 22=4 [13,14] (рис. 3). Ее представимость в виде двойной диаграммы Хассе вытекает из выполнения условий F£tB£tT, F£tN£tT и N£iT£iB, N£iF£iB. Отметим, что в случае бирешетки 4 условие связи между порядками £t и £ i выражается через отрицание Белнапа: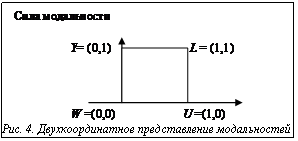 Путем соединения двух подобных моделей sv и sm получаем интегральную модель мнения агента в виде тройки bel(p)=áp,v(p),m(p)ñ, где pÎ P, v:P®V4, m:P®M4, V4={T,F,B,N}, М4={L,U,W,Y}. В частном случае, когда имеем V2={T, F} и М2={L,W}, интерпретация предложенной модели мнения агента сводится к четырем модализированным значениям истинности по Н. Решеру: LT – «необходимая истина»; WТ – «случайная истина»; WF – «случайная ложь»; LF – «необходимая ложь». Отметим, что в четырехзначной логике Решера имеются два выделенных значения: LT и WТ.
Путем соединения двух подобных моделей sv и sm получаем интегральную модель мнения агента в виде тройки bel(p)=áp,v(p),m(p)ñ, где pÎ P, v:P®V4, m:P®M4, V4={T,F,B,N}, М4={L,U,W,Y}. В частном случае, когда имеем V2={T, F} и М2={L,W}, интерпретация предложенной модели мнения агента сводится к четырем модализированным значениям истинности по Н. Решеру: LT – «необходимая истина»; WТ – «случайная истина»; WF – «случайная ложь»; LF – «необходимая ложь». Отметим, что в четырехзначной логике Решера имеются два выделенных значения: LT и WТ. Другие определения связей между модальностями: U=LÚW (cлабая положительная модальность выражается как дизъюнкция сильной положительной и слабой отрицательной), а W=ùLÙùY= ù(LÚY) (слабая отрицательная модальность есть антидизъюнкция сильной положительной и сильной отрицательной модальности).
Другие определения связей между модальностями: U=LÚW (cлабая положительная модальность выражается как дизъюнкция сильной положительной и слабой отрицательной), а W=ùLÙùY= ù(LÚY) (слабая отрицательная модальность есть антидизъюнкция сильной положительной и сильной отрицательной модальности).