Введение. Для учета требований по целостности сигнала в межсоединениях радиоэлектронных средств при их производстве необходимо предварительное моделирование межсоединений с помощью специализированных программных средств. Поскольку одним из основных типов межсоединений являются различные линии передачи, повышение скорости передачи данных и плотности монтажа приводит к необходимости учета электромагнитных связей между всеми близко расположенными проводниками, а также их моделирования как многопроводных линий передачи (МПЛП) [1, 2]. Моделирование МПЛП при помощи аналитических методов из-за сложности их структуры на практике часто неприменимо, поэтому обыч- но используется квазистатическое приближе- ние, в ходе которого выполняется расчет (экстракция) параметров (матриц погонных коэффициентов электростатической L и электромагнитной C индукции, сопротивлений R и проводимостей G) [1] с применением численных методов. Один из наиболее популярных и универсальных из них – метод моментов [3, 4]. В двумерном случае моделируется поперечное сечение исследуемой линии, в котором границы раздела сред (проводник–диэлектрик и диэлектрик–диэлектрик) разбиваются на сегменты для последующего расчета взаимовлияний. При этом некорректный выбор сегментации может привести к существенной погрешности при расчете параметров МПЛП. Так, малое число сегментов приводит к низкой точности аппроксимации распределения зарядов на поверхности проводников, например, к возникновению скачкообразных переходов, а излишне большое – к существенному увеличению вычислительных затрат из-за того, что раз- мерность итогового матричного уравнения равна числу сегментов (N), а вычислительная сложность составляет О(N2).
Подходы к сегментации в разных програм- мных средствах различаются. Так, в ряде средств на основе метода моментов, например, в программах PathWave ADS и FasterCap, доступна только автоматическая сегментация, в других, таких как CONMTL и LINPAR, по умолчанию используется автоматическая сегментация с возможностью ее ограниченной модернизации. Поскольку автоматическая сегментация часто может быть неоптимальной, для эффективного анализа программное средство должно поддерживать как различные виды адаптивной сегментации, так и ручную сегментацию вплоть до указания числа сегментов для каждой границы. Кроме того, в популярных программных средствах, как правило, отсутствует проверка корректности элементов матриц. Тогда вычисленные матрицы L, C, R и G выводятся как есть, без проверки их физичности, которая возлагается на пользователя (о чем, например, сообщается в документации программы PathWave ADS). При этом критерии физичности хорошо известны, а способы программной проверки достаточно тривиальны.
Технологические вариации геометрических параметров МПЛП, анализ температурных зависимостей и прочее требуют многократной экстракции погонных параметров, то есть многовариантного анализа. Для последующей же обработки множества экстрагированных параметров требуется статистический анализ.
Цель данной работы – представить прототип программного средства расчета (экстракции) погонных параметров МПЛП, отличающегося наличием модулей равномерной и неравномерной сегментации, проверки проектных норм экстрагированных параметров, а также многовариантного и статистического анализа.
Метод моментов
При анализе МПЛП с помощью метода моментов рассматривается уравнение Пуассона–Лапласа [5] в интегральном виде:
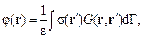
где s – поверхностная плотность заряда; r и r' – точки наблюдения и источника соответствен- но; dG – дифференциал по поверхности МПЛП; ε – диэлектрическая проницаемость; G(r, r') – функция Грина.
В данной постановке задачи считаются заданными граничные условия по приложенному напряжению φ, при этом требуется найти поверхностную плотность заряда σ. Для двумерного случая функция Грина имеет вид
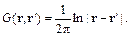 (1)
(1)
При отсутствии в структуре анализируемой МПЛП бесконечной плоскости земли для корректного моделирования в ней должен присутствовать как минимум один опорный проводник. В этом случае для проводниковых границ (1) записывается как
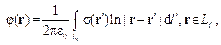 (2)
(2)
где LC – контур проводниковых границ; dl' – элемент этого контура, а для диэлектрических границ получается
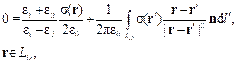 (3)
(3)
где LD – контур диэлектрических границ; n – вектор внешней нормали; ε1 и ε2 – диэлектрические проницаемости с одной (на которую направлен n) и другой (от которой направлен n) сторон границы.
С использованием аппарата базисных и тестовых функций выражения (2) и (3) сводятся к матричному уравнению вида
ZS = Ф, (4)
где Z – матрица размера N ´ N, описывающая МПЛП через связи сегментов ее границ между собой; Ф – матрица размера N ´ M, содержащая известные потенциалы на проводниках; S – матрица размера N ´ M, содержащая неизвестные общие (соответственно свободные и поляризационные) плотности заряда на этих сегментах; N – число базисных и тестовых функций, число сегментов расчетной сетки; M – число проводников МПЛП, не считая опорного.
Матричное уравнение (4) может быть решено прямым или итерационным методом, использующим последовательные приближения для получения более точного решения на каждой следующей итерации. Из решения (4) плотность свободных зарядов SF вычисляется как
SF = erS, (5)
где er – относительная диэлектрическая проницаемость диэлектрика, к которому направлен вектор нормали от границы проводника.
Матрица C, содержащая коэффициенты электростатической индукции, вычисляется из
SF = СФ. (6)
Для получения значения cij нужно заземлить все проводники на опорный, кроме j-го, на который подается напряжение vj, и определить заряд qi на проводнике i. При этом на остальных проводниках будет минус qi. В результате процесс вычисления элементов матрицы может быть представлен как M расчетов двухпроводной емкости, где остальные (M – 1) проводники полагаются под одним потенциалом с опорным, а (4) служит для расчета зарядов на проводниках по заданным потенциалам.
При моделировании без учета потерь, кроме матрицы C, также вычисляется матрица коэффициентов электромагнитной индукции L как
L = μ0ε0C0–1, (7)
где C0 – матрица, полученная по тому же алгоритму, что и C, но при удалении из структуры диэлектрических границ (линия с воздушным заполнением), а μ0 и ε0 – магнитная и электрическая постоянные.
Программная реализация
Прототип программного средства расчета первичных погонных параметров МПЛП по (1)–(7) разработан с использованием синтаксиса интерпретируемого языка программирования MATLAB, совместимого с GNU Octave. В его составе шесть независимых модулей:
– построение геометрической модели поперечного сечения МПЛП (М1);
– сегментация границ поперечного сечения МПЛП (М2);
– формирование и решение матричного уравнения (М3);
– расчет (экстракция) параметров (матрицы C и L) (М4);
– проверка корректности элементов матриц (М5);
– многовариантный и статистический анализ (М6).
 Каждый модуль получает данные и возвращает результат в заданных форматах. Схема взаимодействия модулей представлена на рисунке 1.
Каждый модуль получает данные и возвращает результат в заданных форматах. Схема взаимодействия модулей представлена на рисунке 1.
Модель поперечного сечения МПЛП задается в виде комбинации геометрических примитивов: прямоугольник, многоугольник и эллипс. Для их построения на вход модуля M1 подаются массивы rect, poly и ellip соответственно. Каждая замкнутая фигура образует область (электрически- и магнитнооднородную площадь).
Массив rect имеет размерность M×4, где M – число прямоугольников, каждый из которых определяется четырьмя координатами: минимальная и максимальная абсциссы, минимальная и максимальная ординаты. Трехмерный массив poly имеет размерность 2×L×M, где M – число многоугольников, а L – число линейных сегментов (граней) M-го многоугольника. Для каждой грани первой строкой массива указываются все абсциссы точек, а второй – ординаты. Массив ellip имеет размерность M×5, где M – число эллипсов. Для каждого из них последовательно указываются координаты центра (абсцисса и ордината), длины большой и малой полуосей и вращательный угол (в радианах). Кроме того, на входе модуля M1 для каждой области задается значение относительной диэлектрической проницаемости εr внутри нее. После окончания работы модуля M1 реализующая его функция возвращает структуру данных str (размерностью 10×N, где N – общее число границ), содержащую следующие поля: s – номер начальной вершины границы (поперечного сечения); e – номер конечной вершины границы; d – номер области, к которой относится граница; cx – абсцисса центра границы; cy – ордината центра границы; h – длина границы; nx – горизонтальная компонента единичного вектора нормали к границе; ny – вертикальная компонента единичного вектора нормали к границе; ein – значение εr внутри области (против вектора нормали); eout – значение εr снаружи области (по вектору нормали).
Структура данных str передается на вход модуля M2, где реализуется сегментация границ поперечного сечения МПЛП. Так, доступна равномерная сегментация, при которой пользователь может выбрать только максимальный размер сегмента, и ряд неравномерных, у которых доступны дополнительные параметры. При использовании равномерной сегментации каждая граница разбивается на сегменты равной длины. Их число определяется путем округления в большую сторону частного от деления длины границы на заданный пользователем максимальный размер сегмента. Реализованы два вида неравномерной сегментации: с учащением в углах [6] и проекционная. Также в модуле M2 реализована возможность автоматического итерационного учащения сегментации. Доступны три варианта учащения сегментов на каждой итерации: всех (разбиение каждого сегмента пополам); длина которых превышает установленное пороговое значение [7]; с наибольшей плотно-стью заряда [5], используя информацию из модуля М4.
 Различные методы сегментации и ее учащения могут быть скомбинированы. На выходе модуля М2 используется та же структура данных, что и у М1, но в ней описаны не границы, а их сегменты. Сегментация границ поперечного сечения может быть отображена графически. Около каждого сегмента по желанию пользователя отображаются номер сегмента, номер области, к которой относится сегмент, относительные диэлектрические проницаемости сред слева и справа от сегмента, направление вектора нормали. Примеры итоговой сегментации приведены на рисунке 2.
Различные методы сегментации и ее учащения могут быть скомбинированы. На выходе модуля М2 используется та же структура данных, что и у М1, но в ней описаны не границы, а их сегменты. Сегментация границ поперечного сечения может быть отображена графически. Около каждого сегмента по желанию пользователя отображаются номер сегмента, номер области, к которой относится сегмент, относительные диэлектрические проницаемости сред слева и справа от сегмента, направление вектора нормали. Примеры итоговой сегментации приведены на рисунке 2.
В модуле М3 формируется и решается матричное уравнение (4). При решении уравнений небольшого размера и с плотной матрицей, как правило, используются прямые методы, такие как метод Гаусса или его модифицированная версия, основанная на LU-разложении [8]. Однако для больших матричных уравнений прямые методы вычислительно затратны, поэтому применяются итерационные. Для прямых методов затраты времени на решение матричного уравнения соответствуют O(N3), а машинной памяти – O(N2). Для итерационных методов эти затраты, как правило, ниже и зависят от требуемой точности. Еще одной особенностью итерационных методов является то, что получаемая погрешность решения из-за конечного числа разрядов намного меньше, чем в методе Гаусса, так как она не накапливается, а определяется только последней итерацией и не зависит от их числа. Поэтому решение с заданной точностью при росте числа обусловленности матрицы достигается просто увеличением числа итераций.
Для больших матричных уравнений с несимметричными матрицами часто используют методы крыловского типа [9]. В основном они сводятся к генерации подходящего базиса векторного пространства, называемого подпространством Крылова, и к выбору фактической итерации в пределах этого пространства. Достаточно популярными методами крыловского типа являются стабилизированный метод бисопряженных градиентов (BiCGStab), метод обобщенных минимальных невязок (GMRES), метод индуцированного уменьшения размерности (IDR) и его модификация IDR(S) [9, 10].
Для решения последовательности матричных уравнений, что актуально при использовании многовариантного анализа (модуль М6), целесообразно использовать блочные версии итерационных методов, иначе возникает необ- ходимость последовательных раздельных вычислений с каждой правой частью. Это дополнительно увеличивает вычислительные затраты [9]. Поэтому в модуле М3 реализованы метод LU-разложения (встроенная в MATLAB/ GNU Octave версия) и блочные версии методов BiCGStab, IDR(S) и GMRES [11, 12] (авторские реализации).
Модуль М4 получает на вход матрицу S, вычисленную в модуле М3, реализует вычисления по (5)–(7) и возвращает (передает модулю М5) рассчитанные матрицы C и L.
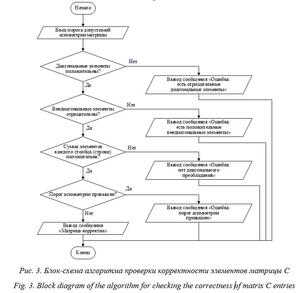
 Модуль М5 проверяет корректность элементов матриц в соответствии с блок-схемами, приведенными на рисунках 3 и 4, и выводит соответствующие сообщения.
Модуль М5 проверяет корректность элементов матриц в соответствии с блок-схемами, приведенными на рисунках 3 и 4, и выводит соответствующие сообщения.
Модуль М6 позволяет выполнять многовариантный анализ параметров МПЛП. При варьировании любого параметра МПЛП модуль автоматически итерационно запускает остальные модули, позволяя получать на выходе набор матриц C и L. Далее над этим набором может быть выполнен статистический анализ с расчетом основных статистических характеристик.
Верификация программного средства расчета первичных погонных параметров
Верификация разработанного прототипа программного средства выполнена на примере двухпроводной микрополосковой линии передачи (далее – ЛП1) со следующими параметрами [13]: ширина проводников w = 2,35 мм;расстояние между проводниками s = 0,65 мм; толщина проводников t = 35 мкм; толщина ди- электрического слоя h = 1,5 мм; расстояние от проводников до границ структуры d = 9,825 мм; εr = 5,18. Ее поперечное сечение представлено на рисунке 5. Для вычисления матриц C и L использованы программные средства PathWave ADS, CONMTL, Ansys Q2D Extractor, а также численно-аналитический метод конформных отображений (МКО) с помощью интеграла Кристоффеля–Шварца [13]. Полученные матрицы отображены в таблице 1. Также в ней указаны параметры сегментации.
Дополнительно выполнена верификация на примере более сложной МПЛП (далее – ЛП2), поперечное сечение которой представлено на рисунке 6. Ее параметры [14]: w = 0,2 мм, t = 0,1 мм, h = 0,1 мм, h1 = 0,5 мм, h2 = 0,4 мм, h3 = 9,1 мм, d = 1,5 мм, εr1 = 6,8, εr2 = 4,5, εr3 = 1. В таблице 2 представлены экстрагированные матрицы.
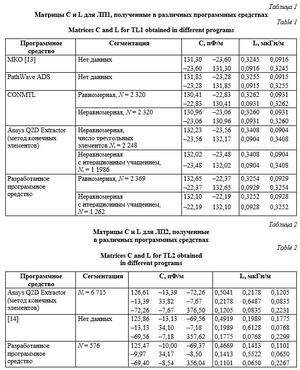
 Как видно из таблиц 1 и 2, параметры, экстрагированные в разработанном прототипе программного средства, хорошо согласуются с аналогичными параметрами в других программных средствах. Так, относительное различие по элементу c11 для ЛП1 не превышает 2 %, для ЛП2 – 1 %.
Как видно из таблиц 1 и 2, параметры, экстрагированные в разработанном прототипе программного средства, хорошо согласуются с аналогичными параметрами в других программных средствах. Так, относительное различие по элементу c11 для ЛП1 не превышает 2 %, для ЛП2 – 1 %.
Выполним многовариантный анализ для ЛП1. Для этого последовательно варьируются геометрические параметры w и t в диапазоне от –7 % до 7 % с шагом 1 % (всего по 15 вариаций). Общее число вычислений (число экстрагированных матриц C и L) составило 225. По экстрагированным матрицам выполнен статистический анализ (вычислены характеристики: математическое ожидание E, дисперсия D, среднеквадратическое отклонение σ и довери- тельный интервал δ), представленный в таблице 3. Как видно, все среднеквадратические отклонения находятся в диапазоне 1–3 % от среднего значения (E), при этом наименьшее значение σ наблюдается у c12 (1,2 %).
Таблица 3
Статистические характеристики для элементов матриц C и L ЛП1
Table 3
Statistical characteristics for the entries of TL1 matrices C and L
|
Элемент матрицы
|
E
|
D
|
σ
|
δ
|
|
c11
|
130,60, пФ/м
|
11,492, (пФ/м)2
|
3,390, пФ/м
|
0,445, пФ/м
|
|
c12
|
–22,84, пФ/м
|
0,069, (пФ/м)2
|
0,264, пФ/м
|
0,035, пФ/м
|
|
l11
|
0,3250, мкГн/м
|
56,160, (нГн/м)2
|
7,494, нГн/м
|
0,979, нГн/м
|
|
l12
|
0,0911, мкГн/м
|
7,885, (нГн/м)2
|
2,808, нГн/м
|
0,369, нГн/м
|
Заключение
Таким образом, с использованием синтаксиса интерпретируемого языка программирования MATLAB, совместимого с GNU Octave, разработан прототип программного средства расчета первичных погонных параметров МПЛП (матриц L и C) и проверки корректности их элементов. Разработанный прототип состоит из шести модулей, первые пять из которых являются полностью самостоятельными, а шестой выполняет их последовательный запуск. Разработанный прототип верифицирован с использованием ряда существующих программных средств. В дальнейшем на его основе планируется создание программного комплекса экстракции параметров на низкоуровневом языке программирования. Кроме того, модульность прототипа позволяет использовать его отдельные модули, в частности, для академических задач.
Список литературы
1. Paul C.R. Analysis of multiconductor transmission lines. Hoboken, New Jersey, John Wiley & Sons Publ., 2007, 803 p.
2. Belousov A.O., Chernikova E.B., Samoylichenko M.A. et al. From symmetry to asymmetry: The use of additional pulses to improve protection against ultrashort pulses based on modal filtration. Symmetry, 2020, vol. 12, no. 7, art. 1117. doi: 10.3390/sym12071117.
3. Makarov S.N., Noetscher G.M., Nazarian A. Low-frequency electromagnetic modeling for electrical and biological systems using MATLAB. Hoboken, New Jersey, John Wiley & Sons Publ., 2015, 616 p.
4. Gibson W.C. The method of moments in electromagnetics. Boca Raton, Chapman & Hall/CRC Publ., 2021, 272 p.
5. Maksimov A.E., Kuksenko S.P. Accurate capacitance matrices for multiconductor transmission lines. IEEE Transactions on Electromagnetic Compatibility, 2022, vol. 64, no. 5, pp. 1514–1521. doi: 10.1109/TEMC.2022.3175717.
6. Maksimov A., Kuksenko S. Adaptive segmentation of multiconductor transmission lines in quasi-static analysis by the method of moments. JPCS, 2021, vol. 1862, no. 1, art. 012020. doi: 10.1088/1742-6596/1862/1/012020.
7. Максимов А.Е., Куксенко С.П. Адаптивный итерационный выбор оптимальной сегментации при решении электростатических задач методом моментов // СИБРЕСУРС-26-2020: матер. Междунар. науч.-практич. конф. 2020. С. 112–116.
8. Gu Z., Wu H., Zhao X., Zhang Y. New LU decomposition accelerating parallel method of moments and its application. Proc. IEEE MTT-S IWS, 2018, pp. 1–3. doi: 10.1109/IEEE-IWS.2018.8400942.
9. Meurant G., Tebbens J.D. Krylov methods for nonsymmetric linear systems: From theory to computations. Berlin, Heidelberg, Springer Publ., 2020, 691 p. doi: 10.1007/978-3-030-55251-0.
10. Kehl R., Nabben R., Szyld D.B. Adaptive multilevel Krylov methods. ETNA, 2017, vol. 51, pp. 512–528. doi: 10.1553/etna_vol51s512.
11. Daas H., Grigori L., Hénon P., Ricoux P. Enlarged GMRES for solving linear systems with one or multiple right-hand sides. IMA J. of Numerical Analysis, 2019, vol. 39, no. 4, pp. 1924–1956. doi: 10.1093/imanum/dry054.
12. Sun D.L., Huang T.Z., Jing Y.F., Carpentieri B. A block GMRES method with deflated restarting for solving linear systems with multiple shifts and multiple right-hand sides. Numerical Linear Algebra with Applications, 2018, vol. 25, no. 5, art. e2148. doi: 10.1002/nla.2148.
13. Стручков С.М., Сычев А.Н. Методика измерения погонных параметров симметричных связанных линий // Электронные средства и системы управления: матер. Междунар. науч.-практич. конф. 2015. № 1-1. С. 159–163.
14. Musa S.M., Sadiku M.N.O. Application of the finite element method in calculating the capacitance and inductance of multiconductor transmission lines. Proc. IEEE SoutheastCon, 2008, pp. 300–304. doi: 10.1109/SECON.2008.4494308.
References
1. Paul, C.R. (2007) Analysis of Multiconductor Transmission Lines. Hoboken, New Jersey: John Wiley & Sons Publ., 803 p.
2. Belousov, A.O., Chernikova, E.B., Samoylichenko, M.A. et al. (2020) ‘From symmetry to asymmetry: The use of additional pulses to improve protection against ultrashort pulses based on modal filtration’, Symmetry, 12(7), art. 1117. doi: 10.3390/sym12071117.
3. Makarov, S.N., Noetscher, G.M., Nazarian, A. (2015) Low-frequency Electromagnetic Modeling for Electrical and Biological Systems Using MATLAB. Hoboken, New Jersey: John Wiley & Sons Publ., 616 p.
4. Gibson, W.C. (2021) The Method of Moments in Electromagnetics. Boca Raton, Chapman & Hall/CRC Publ., 272 p.
5. Maksimov, A.E., Kuksenko, S.P. (2022) ‘Accurate capacitance matrices for multiconductor transmission lines’, IEEE Transactions on Electromagnetic Compatibility, 64(5), pp. 1514–1521. doi: 10.1109/TEMC.2022.3175717.
6. Maksimov, A., Kuksenko, S. (2021) ‘Adaptive segmentation of multiconductor transmission lines in quasi-static analysis by the method of moments’, JPCS, 1862(1), art. 012020. doi: 10.1088/1742-6596/1862/1/012020.
7. Maksimov, A.E., Kuksenko, S.P. (2020) ‘Adaptive iterative selection of optimal segmentation in solving electro-static problems by the method of moments’, Proc. Int. Sci. and Pract. Conf. Natural and Intellectual Resources of Siberia, pp. 112–116 (in Russ.).
8. Gu, Z., Wu, H., Zhao, X., Zhang, Y. (2018) ‘New LU decomposition accelerating parallel method of moments and its application’, Proc. IEEE MTT-S IWS, pp. 1–3. doi: 10.1109/IEEE-IWS.2018.8400942.
9. Meurant, G., Tebbens, J.D. (2020) Krylov Methods for Nonsymmetric Linear Systems: From Theory to Computations. Berlin, Heidelberg: Springer Publ., 691 p. doi: 10.1007/978-3-030-55251-0.
10. Kehl, R., Nabben, R., Szyld, D.B. (2017) ‘Adaptive multilevel Krylov methods’, ETNA, 51, pp. 512–528. doi: 10.1553/etna_vol51s512.
11. Daas, H., Grigori, L., Hénon, P., Ricoux, P. (2019) ‘Enlarged GMRES for solving linear systems with one or multiple right-hand sides’, IMA J. of Numerical Analysis, 39(4), pp. 1924–1956. doi: 10.1093/imanum/dry054.
12. Sun, D.L., Huang, T.Z., Jing, Y.F., Carpentieri, B. (2018) ‘A block GMRES method with deflated restarting for solving linear systems with multiple shifts and multiple right-hand sides’, Numerical Linear Algebra with Applications, 25(5), art. e2148. doi: 10.1002/nla.2148.
13. Struchkov, S.M., Sychev, A.N. (2015) ‘Methodology for measuring linear parameters of symmetrical coupled lines’, Proc. Int. Sci. and Pract. Conf. Electronic Means and Control Systems, (1-1), pp. 159–163 (in Russ.).
14. Musa, S.M., Sadiku, M.N.O. (2008) ‘Application of the finite element method in calculating the capacitance and inductance of multiconductor transmission lines’, Proc. IEEE SoutheastCon, pp. 300–304. doi: 10.1109/SECON. 2008.4494308.
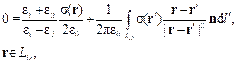 (3)
(3)





