Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , Bobkov V.I. (vovabobkoff@mail.ru) - Branch of the National Research University "MPEI" in Smolensk (Head of Department), Smolensk, Russia, Ph.D, Orekhov V.A. (fundukoff@mail.ru) - Branch of the National Research University "MPEI" in Smolensk (Assistant), Smolensk, Russia, () - | |
| Page views: 33 |
Print version |
Введение. Математическое моделирование процессов в рудовосстановительных электротермических реакторах для получения сплавов фосфатного сырья позволяет выявить условия оптимального функционирования и снижения затрат на единицу получаемой продукции [1, 2]. Работ, отвечающих всем требованиям физики процессов, протекающих в реакторах подобного типа, весьма немного, например [3, 4]. Российскими и зарубежными исследователями предпринимались различные попытки моделирования процессов, происходящих в реакторах такого типа, но представленные модели являлись либо однофакторными, либо настолько математическими сложными, что при их реализации в компьютерной программе возникали сложности. В работах российских ученых [5, 6] представлены одномерные модели и ПО для расчета процессов, происходя- щих только в реакторной зоне руднотермических печей, используемых для получения желтого фосфора. Сами авторы отмечают, что их разработка может быть использована как составляющая часть программного комплекса расчета технологического процесса. Зарубежными учеными также в основном рассматриваются однофакторные модели, учитывающие только один параметр реактора, в частности, температуру рабочей поверхности электродов, электрический потенциал или тепловые коэффициенты восстановительного процесса [7, 8]. Между тем необходимы технологический расчет реактора в целом и реализация возможности анализа руднотермических печей, используемых в различных отраслях металлургической промышленности. Рассматриваемые технологические установки характеризуются протеканием сложных тепломассообменных явлений, для анализа которых требуется применение многофакторных математических моделей [9]. Таким образом, создание адекватной математической модели даст возможность не только более основательно обследовать процессы, происходящие внутри данных реакторов, но и разработать системы автоматизации расчетов, способствующие модернизации данных установок с целью повышения их энергетической эффективности. Разработанная модель тепломассопереноса в исследуемых реакторах содержит уравнения движения фаз, тепломассообмена и распределения электрического потенциала. Реализация данного метода расчета параметров функционирования восстановительных реакторов дает возможность решения системы уравнений тепломассопереноса свести к решению уравнений теплопроводности и диффузии, что существен- но облегчает реализацию поставленной задачи. Таким образом, в зоне реакции и образования шлака уравнения тепломассопереноса мож- но представить в следующем виде: div(λT gradTf) + qve – qcrωcr = 0, div(DT gradCf) – ωcr = 0, а уравнение распределения электрического потенциала как div((1/ρe)gradφe) = 0. Процессы теплообмена в шихтовой зоне описываются в приближении Дарси уравнениями энергопереноса [10]: (1 – ε)cmρmvmgradTm – div(λmgradTm) = = αv(Tg – Tm),
div(gradjm) = 0, vm = –gradjm, div(kgradjg) = γωcr, vg = –kgradjg, где λT – эффективная теплопроводность расплава; qcr – тепловой эффект восстановительного процесса; Tf – температура расплава; Cf – концентрация реагента. Для углеродистой зоны граничные условия можно задать следующим образом: Г Î Гmelt, Tf = Tmelt, на стенках реактора:
для переноса массы: Г Î Гmelt, C = Cm. Условие для стенок (непроницаемость):
При наличии многослойной зоны для электрического потенциала граничные условия оп- ределяются для каждого компонента на поде: Г Î Гd, je = 0, на поверхности электрода: Г Î Гe, je = jeэ, на границе расплав–шихта:
на границе раздела k-й и k+1-й электропроводящих зон расплава:
На верхней границе температурные граничные условия шихты имеют вид Г Î Гm, Tm = Tenv, в зоне плавления минеральных компонентов шихты: Г Î Гmelt, Tm = Tmelt. На выходе в зоне реакции температуру газа можно задать как среднюю температуру расплава в надлежащем сечении: Tg = Tf. Таким образом, на фронте плавления сход шихты определяется следующим граничным условием:
Учитывая непроницаемость стенок реактора, получаем следующее граничное условие:
где T0 – температура охладителя реактора; Tmelt – температура плавления шихты; Tenv – температура верхней границы шихтовой зоны; khe – коэффициент теплопередачи, в случае идеальной изоляции градиент температуры равен нулю; Qmelt – количество теплоты, необходимое для плавления шихты; Cm – концентрация реагента в шихте; ρm – насыпная плотность шихты.
Построение математической модели итерационного алгоритма расчета руднотермической установки
В представленной модели используются элементы четырехугольной формы с базисными функциями с непрерывностью первого порядка, поскольку они наиболее предпочтительны для решения уравнений конвективного теплообмена [11]. Искомая непрерывная величина в области четырехугольного конечного элемента представляется в виде
где Фi – неизвестные значения искомой величины в узлах конечного элемента; Ni – базисные функции элемента. На конечном элементе вводится локальная система координат (x, h), где –1 £ x £1, –1 £ h £ 1, которая позволяет использовать элементы нестандартной формы, а также упрощает интегрирование уравнений. Преобразование этой системы в декартовую систему координат (x, y) выглядит следующим образом:
где xi и yi – координаты узлов конечного элемента. Базисные функции элемента с использованием локальной системы координат имеют вид
Для вычисления производных в координатах (x, h) используется соотношение
где якобиан [J] вычисляется по формуле
Для решения дифференциальных уравнений совместно с методом конечных элементов используется метод Галеркина, заключающийся в том, что искомое решение будет наилучшим, если интеграл взвешенной невязки равен нулю:
где L(x) = 0 – интегрируемое дифференциальное уравнение. Для вычисления интегралов используется численное интегрирование с использованием квадратурных формул Ньютона–Котеса в локальных координатах элемента:
где n = 4 – количество точек интегрирования; Нk = 1 – весовые коэффициенты, заданные для точек с локальными координатами xk = ±0,577350; hk = ±0,577350; f – интегрируемая функция. Полученные в результате интегрирования матрицы систем уравнений для каждого элемента объединяются в одну систему уравнений для всей области. Для генерации сетки конечных элементов используется метод суперэлементов. При использовании этого метода в исходной области вводится нерегулярная сетка криволинейных восьмиузловых четырехугольников, которые называются суперэлементами S с узлами Pi = P(xis, yis), I = 1, 2, ..., 8. При помощи отображения x(xh) = xisNi, y(xh) = yisNi(xh) квадрат Q отображается в S, где Ni(x, h) – квадратичные базисные функции на суперэлементе:
Построенная в Q равномерная сетка отображается в криволинейную сетку суперэлемента S. При этом расположение узловых точек Pi на сторонах позволяет осуществлять локальное сгущение сетки. Объединение сеток, построенных таким образом на каждом суперэлементе, дает сетку на всей исходной области, как показано на рисунке 1. На рисунке 2 представлена сетка четырехугольных конечных элементов, сгенерированная для модели электротермического рудовосстановительного реактора. При этом границы суперэлементов выбирались на границах расчетных зон. Границы электродов аппроксимировались параболой. Уравнения математической модели реактора можно привести к двум следующим формам: div(k gradФ) – q = 0, V gradФ – div(k gradФ) + q = 0. (1) Аппроксимирующую систему уравнений можно представить в следующем виде: [A][Ф] = [F], (2) где [F] – вектор свободных членов, [А] – матрица системы уравнений. На основе теоремы Грина и квадратурных формул численного интегрирования для уравнения (2) матрица системы уравнений задается как
где
Вектор свободных членов определяется следующим образом:
При этом матрицы определяются в соответствующих точках (xk, hk) конечного элемента. Для аппроксимации уравнений типа (1) при больших значениях отношения v/k используется модифицированный метод Галеркина, из- вестный под названием метода Петрова–Галеркина, являющийся конечноэлементным аналогом метода конечных разностей с разностями вверх по потоку [12, 13]. При этом в качестве весовых функций используются функции, отличные от базисной (так называемые асимметричные весовые функции). При этом условие наилучшего решения выглядит как
здесь [W] – вектор асимметричных весовых функций, принимаемых в виде
где aij – коэффициенты степени асимметричности (индексы определяют номера узлов конечного элемента, соединяемых соответствующи- ми сторонами), оптимальное значение которых определяется из выражения
Сеточное число Пекле Pe определяется по формуле
где hij – длина стороны конечного элемента, соединяющей узлы i, j; Vср – средняя скорость вдоль этой стороны, определяемая как
где Vi и Vj – значения вектора скорости в узлах i и j; Iij – вектор направления стороны ij. При использовании асимметричных базисных функций матрица системы линейных уравнений, аппроксимирующей дифференциальное уравнение, будет определяться следующим образом:
где Вектор свободных членов:
Результирующая матрица системы уравнений в методе конечных элементов является разреженной. Для решения таких систем уравнений в течение продолжительного времени использовались прямые методы типа метода исключения Гаусса с выбором исключающего элемента и с учитом разреженности и ленточной структуры матрицы [14]. При этом большое внимание уделялось использованию алгоритмов перенумерации узлов сетки, минимизирующих ширину ленты, позволяющих сократить объем памяти ЭВМ, необходимой для хранения матрицы, и время расчета [15]. Матрицы системы линейных уравнений, аппроксимирующие дифференциальные уравнения диффузии, уравнения типа (1), являются симметричными, положительно определенны- ми и хорошо решаются прямыми методами. В отличие от них матрицы систем, аппрок- симирующие дифференциальные уравнения с конвективными членами, уравнения типа (1), не имеют регулярной структуры, несимметрич- ны, неположительно определены и являются плохо обусловленными, что ограничивает применение прямых методов для решения таких систем. Кроме того, для увеличения точности необходимо увеличивать количество узлов расчетной сетки конечных элементов и, следовательно, увеличивать размерность систем урав- нений, для которых нельзя применять прямые методы решения из-за нарастающих ошибок округления, связанных с выполнением большого числа арифметических операций. Для устранения этих трудностей необходимо использовать итерационные методы. Данный метод формирования математической модели позволяет на основе применения управляющих параметров определить закономерности изменения температуры газов, возникающих в подсводной области реактора.
Итерационный алгоритм реализации математической модели расчета электротермических установок
В основе построения алгоритма лежит метод сопряженных градиентов. Данный метод адаптирован для решения симметричных положительно определенных систем алгебраических уравнений [16], его обобщение – метод уменьшения размерности (Induced Dimension Reduction – IDR) пригоден как для неcсиммет- ричных, так и для неположительно определенных систем уравнений. Приведем алгоритм метода сопряженных градиентов (IDR) для решения системы уравнений вида [A][X] = [B]. Задаются начальное приближение [X]0 и точность расчета e: 1) [F]0 = [A][X]0 – [B]; [dG]0 = [dY]0 = 0; 2) n = n + 1; 3) [S]n = [F]n-1 + wn-1[dG]n-1; [T]n = [A][S]n; 4) если n = 1 или n четное 5) αn = αn-1; 6) [dX]n = wn-1[dY]n-1 – an [S]n; 7) [dF]n = wn-1[dG]n-1 – an[T]n; 8) [X]n = [X]n-1 + [dX]n; [F]n = [F]n-1 + [dF]n; 9) если n четное, [dG]n = [dG]n-1; [dY]n = [dY]n-1, переход к п.12; 10) [dG]n = [dF]n; [dY]n = [dX]n; 11) 12) если 13) окончание расчета с результатом [X]n. Системы алгебраических уравнений метода конечных элементов, как уже отмечалось, имеют ленточную структуру. При этом время их решения T~b2N, а объем памяти ЭВМ, необходимый для хранения матрицы, V~bN, где N – число неизвестных; b – ширина ленты. Величина b зависит от нумерации узлов сетки и может принимать значения в широком диапазоне: В настоящей работе при хранении матрицы системы уравнений исключаются почти все нулевые (незначимые) коэффициенты. Это достигается использованием двух одномерных массивов, один из которых хранит вещественные значения коэффициентов уравнений, а другой целые номера переменных, соответствующие этим коэффициентам. Для четырехугольных билинейных конечных элементов количество узлов, соседних заданному узлу, не превышает восьми. Таким образом, подобный способ хранения матрицы системы уравнений эквивалентен традиционному с шириной ленты, равной девяти. Этот способ позволяет сократить объем памяти ЭВМ, необходимой для хранения матрицы системы уравнений при N = 1 000 и использовании вещественных чисел с двойной точностью, почти в три раза по сравнению с традиционным и почти в девять раз уменьшить время расчета. Массивы для хранения коэффициентов системы уравнения и номеров соответствующих переменных имеют размерность N ´ M, где М – максимальное количество переменных, входя- щих в уравнение. Приведем алгоритм расчета вектора [F] = [A][X] с использованием предложенного способа хранения матрицы [A]. При этом полагается, что коэффициенты матрицы хранятся в массиве Matr, а номера соответствующих переменных в массиве Index: for(i=0; i<N; i++) { F[i]=0; for(j=0; j<M; j++) { F[i]+=Matr[i*M+j]*X[Index[i*M+j]; } } Для моделирования процессов в электротермическом рудовосстановительном реакторе используется двухмерная математическая модель. При этом рассматриваются сечения, проходящие через центры двух электродов. Расчет тепломассопереноса сводится к решению системы дифференциальных уравнений. Использование метода конечных элементов позволяет аппроксимировать эти уравнения системой алгебраических уравнений. Увеличение количества узлов сетки в силу необходимости повысить точность расчетов и наличие большого количества уравнений, описывающих математическую модель, делает размерность общей системы алгебраических уравнений очень большой, что уменьшает вероятность ее сходимости. Кроме того, система получается нелинейной вследствие вхождения в уравнения величин, определяемых из других уравнений, и плохо обусловленной из-за наличия в исходной системе уравнений конвективного теплообмена. Декомпозиция общей системы на подсистемы, аппроксимирующие отдельные дифференциальные уравнения, и последовательное решение этих систем итерационным методом практически устраняют трудности в реализации задачи. При этом значения величин, входящие в уравнения, берутся из предыдущей итерации. Для получения распределения какой-либо величины сначала формируется система алгебраических уравнений, аппроксимирующих соответствующее диф- ференциальное уравнение, которая затем ре- шается с использованием метода, описанного выше. Критерием окончания расчета является равенство единице количества итераций метода сопряженных градиентов при решении каждой системы уравнений. Уравнение теплообмена в реакционной зоне печи, определяющее распределение температуры, имеет ярко выраженную нелинейность, обусловленную экспоненциальной зависимо- стью скорости реакции восстановления от температуры. Сходимость системы, включающей такое уравнение, ограничена правильным выбором начального приближения. В настоящей работе в качестве начального приближения для определения распределения температуры в реакционной зоне печи используется постоянная температура, равная температуре плавления. Для повышения сходимости системы уравнений используется метод нижней релаксации. При этом распределение температуры на каждой итерации ищется по схеме
где [T]n-1 – распределение температуры, полученное на предыдущей итерации; [T]np – расчетное распределение температуры на текущей итерации, полученное решением соответствующей системы уравнений; 0 < aр < 1 – коэффициент релаксации. На первых итерациях зна- чение коэффициента релаксации выбирается малым aр » 0,01 и в дальнейшем по мере сходимости системы увеличивается либо вручную, либо автоматически с использованием зависимости
где ni – количество итераций метода сопряженных градиентов при решении системы уравнений, аппроксимирующих уравнение теплообмена в реакционной зоне печи; k – коэффициент пропорциональности. Использование в качестве начального приближения результатов предыдущих расчетов позволяет значительно сократить время решения совместной системы уравнений. Для определения интегральных характеристик режима работы объема реактора, таких как полная активная мощность, выход газа и расход шихты, используется положение о том, что основное энерговыделение происходит в приэлектродных областях реакционной зоны. Там же происходит основная часть физико-химических процессов (образование газа и плавление шихты). При этом осуществляется интегрирование для каждого электрода по секторам величиной p с предположением, что тепловыделение на равноудаленной от электрода цилиндрической поверхности равно расчетному значению на том же расстоянии от электрода. Значение полной активной мощности в расчетном сечении ванны печи определяется выражением
где q – удельное объемное энерговыделение; re – расстояние до ближайшего электрода. Интегрирование для трех различных сечений печи позволяет получить полную мощность с учетом взаимодействия электродов между собой при их различных заглублениях и, следовательно, их положений относительно подины. Ее значение выводится из результатов, полученных для каждого сечения, и делением на два, так как влияние каждого электрода учитывается два раза. Аналогично определяются и другие интегральные характеристики режима работы. Перед началом вычисления расчетная область печи разбивается на суперэлементы, а затем генерируется сетка конечных элементов на каждом из них. Путем объединения этих сеток получается сетка конечных элементов для всей расчетной области. После этого формируется массив для хранения систем уравнений. Таким образом, разработанный алгоритм можно представить в следующем виде. 1. Создание системы суперэлементов для расчетной области. 2. Формирование сетки конечных элементов. 3. Формирование массивов для хранения систем уравнений. 4. Формирование системы уравнений для расчета распределения электрического потенциала. 5. Расчет распределения электрического потенциала. 6. Расчет распределения удельного энерговыделения. 7. Формирование системы уравнений для расчета распределения температуры в зоне расплава. 8. Расчет распределения температуры в зоне расплава. 9. Релаксация температуры в зоне расплава. 10. Формирование системы уравнений для расчета распределения концентрации реагента в зоне расплава. 11. Расчет распределения концентрации реагента в зоне расплава. 12. Формирование системы уравнений для расчета распределения потенциала газа. 13. Расчет распределения потенциала газа. 14. Расчет распределения скорости газа. 15. Формирование системы уравнений для расчета распределения потенциала шихты. 16. Расчет распределения потенциала ших- ты. 17. Расчет распределения скорости схода шихты. 18. Формирование системы уравнений для расчета распределения температуры газа в ших- товой зоне печи. 19. Расчет распределения температуры газа в шихтовой зоне печи. 20. Формирование системы уравнений для расчета распределения температуры шихты. 21. Расчет распределения температуры ших- ты. Если при выполнении всех расчетов сходимость достигалась более чем за одну итерацию, переход к п. 3. 22. Расчет интегральных характеристик режима работы печи. Информационная система расчета электротермических реакторов Представленная математическая модель и соответствующий ей алгоритм позволили создать на языке программирования С++ информационную систему моделирования и технологического расчета электротермических установок, применяемых в различных отраслях металлургии. Программный комплекс может функционировать под различными семейства- ми операционных систем, кроме Mac OS, так как создавался с применением кроссплатформенного комплекса Visual Code, позволяющего компилировать программу под большой спектр операционных систем. Информационная система обладает многоза- дачным интерфейсом, позволяющим моделиро- вать различные компоненты исследуемых реакторов. Пользователь может либо выбрать расчет только одного конкретного параметра, либо осуществить комплексный анализ электротермической установки. Для ввода исходных данных используется специальная форма (http://www.swsys.ru/uploaded/image/2024-4/3.jpg). В меню начальные данные включают основные характеристики рудновосстановительных реакторов. При этом от пользователя не требуется введения всех необходимых параметров. Можно ввести только те, которые знает исследователь, или только те, которые ему нужны. В результате система выполнит расчеты на основе введенных данных и выдаст сообщение о невозможности проведения всех запрограм- мированных вычислений. При выборе расчета отдельного параметра можно отыскать необходимый параметр, в случае соответствия вве- денных данных система произведет расчет, в противном случае она укажет на недостаточность введенных данных. Система содержит Результатом компьютеризированного расчета являются численные значения параметров электротермической установки и получение графического распределения данных в виде изолиний и полей векторов (рис. 3). Созданная информационная система позволяет внести проведенные расчеты в БД программы и с помощью сетевого обмена добавить результаты в программный модуль других пользователей по желанию автора, проводившего расчет, тем самым обеспечивая формирование общей научной базы исследований данных видов электротермических установок. Заключение Разработанная математическая модель позволила создать итерационный алгоритм расче- та параметров рудновосстановительных реакторов, применяемых в различных областях черной и цветной металлургии. Данная модель позволяет смоделировать и исследовать труд- нодоступные процессы, происходящие внутри рудновосстановительных реакторов в ходе их функционирования. На основе представленного алгоритма была спроектирована информационная система, позволяющая получить численные значения различных величин, характеризующих происходящие процессы в любой точке ванны руднотермической печи, на- пример, температуру материала, концентрацию реагента, распределение электрического потенциала, температуру газа и др. Кроме численных значений, в программном комплексе реализована возможность графического представления результатов на основе полей изолиний и векторов, что создает научный потенци- ал для формирования математического описания закономерностей происходящих процессов с возможностью компьютерного моделирования исследуемых руднотермических процессов. Представленный программный комплекс использовался для анализа режимов работы плавильных печей, перерабатываюших рудное фосфатное сырье. Сопоставление показателей созданной математической модели с результатами численного анализа работы конкретных агрегатов показало вполне удовлетворительную сходимость. Дальнейшее развитие представленной модели позволит разрабатывать алгоритмы управления и функционирования рудновостановительных реакторов независимо от используемой модели агрегата в производстве. Список литературы 1. Tesser R., Santacesaria E. Revisiting the role of mass and heat transfer in gas–solid catalytic reactions. Processes, 2020, vol. 8, no. 12, art. 1599. doi: 10.3390/pr8121599. 2. Hu H.-P. Theoretical study of convection heat transfer and fluid dynamics in microchannels with arrayed microgrooves. Math. Problems in Engineering, 2021, vol. 2021, art. 601509. doi: 10.1155/2021/3601509. 3. Антипина Е.В., Мустафина С.А., Антипин А.Ф. Программная реализация алгоритма поиска оптимального температурного режима каталитического процесса // Программные продукты и системы. 2022. Т. 35. № 1. С. 106–112. doi: 10.15827/0236-235X.137.106-112. 4. Пучков А.Ю., Лобанева Е.И., Култыгин О.П. Алгоритм прогнозирования параметров системы переработки отходов апатит-нефелиновых руд // Прикладная информатика. 2022. Т. 17. № 1. С. 55–68. doi: 10.37791/2687-0649-2022-17-1-55-68. 5. Пучков А.Ю., Панченко С.В., Черновалова М.В. Программа моделирования теплофизических процессов в руднотермических печах при изменении управляющих воздействий // Программные продукты и системы. 2020. Т. 33. № 3. С. 523–529. doi: 10.15827/0236-235X.131.523-529. 6. Пучков А.Ю., Соколов А.М., Федотов В.В. Нейросетевой метод анализа процессов термической обработки окомкованного фосфатного рудного сырья // Прикладная информатика. 2022. Т. 17. № 5. С. 62–76. doi: 10.37791/ 2687-0649-2022-17-5-62-76. 7. Pedro A.A. Thermal monitoring of the electrode and bath in an ore-roasting furnace during downtime. Steel in Translation, 2013, vol. 43, pp. 110–112. doi: 10.3103/S0967091213020149. 8. Tian H., Pan J., Zhu D., Wang D., Xue Y. Utilization of ground sinter feed for oxidized pellet production and its effect on pellet consolidation and metallurgical properties. In: Minerals, Metals and Materials Series. Proc. Int. Symposium on High-Temperature Metallurgical Processing, 2020, pp. 857–866. doi: 10.1007/978-3-030-36540-0_76. 9. Орехов В.А., Бобков В.И., Панченко С.В. Разработка информационной системы расчета, накопления информации и паспортизации теплофизических свойств фосфоритов // Программные продукты и системы. 2022. Т. 35. № 3. С. 502–508. doi: 10.15827/0236-235X.139.502-508. 10. Орехов В.А. Математическое моделирование процессов образования шлама в рудно-термических печах при переработке фосфатного рудного сырья // Современные наукоемкие технологии. 2023. № 7. С. 78–86. doi: 10.17513/snt.39698. 11. Борисов В.В., Курилин С.П., Луферов В.С. Нечёткие реляционные когнитивные темпоральные модели для анализа и прогнозирования состояния сложных технических систем // Прикладная информатика. 2022. Т. 17. № 1. С. 27–38. doi: 10.37791/2687-0649-2022-17-1-27-38. 12. Курилин С.П., Соколов А.М., Прокимнов Н.Н. Компьютерная программа для эксплуатационной диагностики электромеханических систем на основе топологического подхода // Прикладная информатика. 2021. Т. 16. № 4. С. 62–73. doi: 10.37791/2687-0649-2021-16-4-62-73. 13. Кувшинова А.Н., Цыганов А.В. Программный комплекс для компьютерного моделирования процессов параметрической идентификации математических моделей конвективно-диффузионного переноса // Программные продукты и системы. 2021. Т. 34. № 4. С. 639–648. doi: 10.15827/0236-235X.136.639-648. 14. Свириденко А.Б. Прямые мультипликативные методы для разреженных матриц. Несимметричные линейные системы // Компьютерные исследования и моделирование. 2016. Т. 8. № 6. С. 833−860. doi: 10.20537/2076-7633-2016-8-6-833-860. 15. Пирова А.Ю., Кудрявцев Н.Ю., Мееров И.Б. Экспериментальное сравнение алгоритмов в параллельном многоуровневом методе вложенных сечений // Вестн. ЮУрГУ. Сер.: Вычислительная математика и информатика. 2017. Т. 6. № 1. С. 38–55. doi: 10.14529/cmse170103. 16. Лебедева А.В., Рябов В.М. О численном решении систем линейных алгебраических уравнений с плохо обусловленными матрицами // Вестн. СПбГУ. Математика. Механика. Астрономия. 2019. Т. 6. № 4. С. 619–626. doi: 10.21638/11701/spbu01.2019.407. |
| Permanent link: http://swsys.ru/index.php?id=5126&lang=en&page=article |
Print version |
| The article was published in issue no. № 4, 2024 |
Back to the list of articles
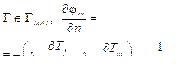
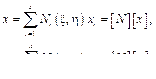
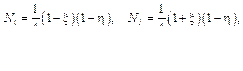
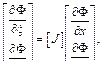
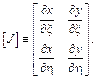
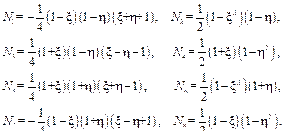
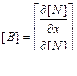 – матрица производных функций формы;
– матрица производных функций формы;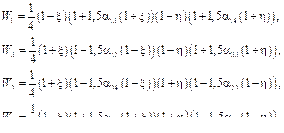
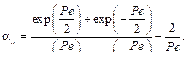
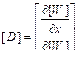 – матрица производных функций формы; [V] – вектор скоростей.
– матрица производных функций формы; [V] – вектор скоростей. 