Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Ключевое слово: |
|
| Page views: 14942 |
Print version Full issue in PDF (1.17Mb) |
Современный этап развития нашей страны характерен тем, что растущие потребности рынка, достижения науки и техники вызывают появление новых технологий, которые не столько расширяют, сколько усложняют, интенсифицируют деятельность в сфере производства. Поэтому особую актуальность приобретает решение задач по повышению эффективности современных систем управления, внедрению современных информационных технологий принятия решений на всех уровнях хозяйственного механизма. Сложность решаемых задач обусловила и появление сложных математических моделей, которые должны адекватно отображать сложность исследуемой системы управления и, прежде всего, ее многоцелевой характер. Отсюда следует, что в основе таких моделей должны лежать многокритериальные задачи оптимизации, и разработка эффективных методов их решения является важнейшей задачей системного анализа. В данной работе предлагаются многокритериальные постановки и соответствующий алгоритм решения актуальных задач, который, как нам кажется, должен стать ядром современных информационных систем бизнес-планирования и управления. Задача оптимального проектирования и оптимальной комплектации Цикл жизни любой системы (технической, экономической, информационной) состоит из ряда этапов, важнейшим из которых является этап проектирования. На этом этапе решается задача оптимального выбора состава и структуры создаваемой системы. Таким образом, содержательная постановка задачи проектирования сложной системы приводит к возможности автоматизации этого процесса с помощью математических моделей векторной оптимизации. Назовем ее задачей оптимальной комплектации и приведем общий вариант ее возможной постановки [1].
В общем случае иерархическая картина функциональной структуризации системы может выглядеть подобно изображенной на рисунке. Будем считать заданными следующие характеристики проектируемой системы (способы их определения для конкретной задачи можно найти в [1]): Тогда, если в качестве переменной выбора взять булеву переменную:
причем
то комплексный показатель эффективности функционирования всей системы Y определится как:
где
Другим важнейшим критерием для выбора окончательного варианта состава проектируемой системы является стоимостная оценка всего проекта С, которая в принятых обозначениях есть
Таким образом, математическая модель задачи оптимальной комплектации проектируемой сложной системы сводится к поиску наилучшей эффективности
при минимуме затрат
причем на переменные модели наложены ограничения (1) и (3). Очевидно, что полученная модель является дискретной задачей векторной оптимизации, и ее решение сможет дать гораздо более полную «картину проектирования», чем интегрированные показатели «затраты/качество», которые используются сейчас. Задача оптимального выбора инвестиционного проекта Пусть в общем случае один из m потенциальных инвесторов выбирает один из n инвестиционных проектов. Пусть также каждый из инвесторов оценивает основные параметры эффективности каждого проекта по своей методике. В качестве таких основных параметров используются четыре показателя инвестиционной эффективности (NPV (net present value) – чистый приведенный доход; PI (profitability index) – индекс рентабельности (доходности); PP (payback period) – срок окупаемости инвестиций; IRR (internal rate of return) – внутренняя норма доходности), методика расчета которых для конкретных схем реализации инвестиционных проектов хорошо известна [2]. Тогда все эти данные могут быть заданы четырьмя квадратными матрицами:
где
где
Задача (8)–(12) является многокритериальным аналогом задачи о назначениях и относится к классу задач дискретной векторной оптимизации. Решение даст возможность потенциальному инвестору сделать оптимальный выбор инвестиционного проекта, учитывая все показатели эффективности. В данной работе предлагается алгоритм решения векторных задач, основанный на методе гарантированного результата и нормализации критериев (ГРНК) [4]. Он отличается от большинства других методов доказательством существования и единственности получаемого оптимального решения по Парето и тем, что его можно использовать для решения различных векторных задач (как линейных, так нелинейных и дискретных). Пусть в общем случае поставлена задача векторной оптимизации:
где
Тогда в соответствии с методом ГРНК необходимо следующее. Шаг 1. Решить Шаг 2. Выполнить единую нормализацию критериев
Шаг 3. Построить
Шаг 4. Решить
или
Шаг 5. Зная величину нормализованного критерия в точке Кроме того, метод ГРНК позволяет решать векторные задачи с приоритетом некоторого критерия, выбранного ЛПР (лицом, принимающим решения) с целью улучшить его значение. При этом уровень приоритета, можно сказать, вычисляется с помощью коэффициентов приоритета, а не назначается ЛПР субъективно, как в подавляющем числе других методов решения векторных задач. Для решения векторной задачи с неравнозначными критериями необходимо в общем случае выполнить следующие шаги. Шаг 6. Решаем соответствующую векторную задачу с равнозначными критериями. ЛПР проводит анализ результатов решения и по величине Шаг 7. Вычисляются пределы изменения коэффициента приоритета s-критерия по отношению к остальным:
где
Шаг 8. ЛПР выбирает необходимую величину
решая которую как скалярную задачу оптимизации, находит точку компромиссного решения
или
Если
решая которую как скалярную задачу оптимизации, можно аналогично найти точку компромиссного решения Шаг 9. Найти компромиссные значения каждого критерия Таким образом, предлагаемый метод ГРНК, используя существующие способы решения задач скалярной оптимизации, может достаточно легко встраиваться в различные алгоритмы принятия решений и, по нашему мнению, должен стать основой современных информационных систем управления. Список литературы 1. Мезенцев Ю.А., Кириллов Ю.В. Некоторые аспекты задач оптимального проектирования при нескольких крите- риях предпочтения. //Сб. науч. тр. НГТУ, 2003.- №3. - С. 21-40. 2. Четыркин Е.М. Финансовый анализ производственных инвестиций. – М.: Дело, 1998. 3. Ковалев В.В. Методы оценки инвестиционных проектов. - М.: ФиС, 1998. 4. Иванов Л.Н., Кириллов Ю.В. К вопросу о Парето-оптимальности решений задач векторной оптимизации // Сб. науч. тр. НГТУ, 2003. - №3. - С. 61-74. |
| Permanent link: http://swsys.ru/index.php?id=556&lang=en&page=article |
Print version Full issue in PDF (1.17Mb) |
| The article was published in issue no. № 1, 2005 |
Perhaps, you might be interested in the following articles of similar topics:
- Целесообразность применения web-служб в распределенных автоматизированных системах военного назначения
- Эволюционная модель формирования структур виртуальных предприятий
- Формирование программ развития больших систем административно-организационного управления
- Формулировка задачи планирования линейных и циклических участков кода
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
Back to the list of articles
 Следуя методике функционально-стоимостного анализа, для оценки эффективности производится последовательная декомпозиция состава проектируемой системы на определенное число уровней детализации в соответствии с основными функциями
Следуя методике функционально-стоимостного анализа, для оценки эффективности производится последовательная декомпозиция состава проектируемой системы на определенное число уровней детализации в соответствии с основными функциями  , выполняемыми подсистемами и вариантами
, выполняемыми подсистемами и вариантами  их возможной реализации.
их возможной реализации. – значимость (вес) j-й функции i-го уровня;
– значимость (вес) j-й функции i-го уровня;  – степень эффективности реализации j-й функции i-го уровня в q-м варианте;
– степень эффективности реализации j-й функции i-го уровня в q-м варианте;  – минимальное допустимое значение степени эффективности реализации j-й функции i-го уровня;
– минимальное допустимое значение степени эффективности реализации j-й функции i-го уровня;  – затраты на осуществление j-й функции i-го уровня в q-м варианте реализации.
– затраты на осуществление j-й функции i-го уровня в q-м варианте реализации.
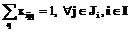 , (1)
, (1) , (2)
, (2) – нормализующий коэффициент, необходимый для приведения разнородных слагаемых в (2) к безразмерному виду. При этом следует гарантировать минимально допустимую степень эффективности реализации отдельных функций, которая определяется техническим заданием:
– нормализующий коэффициент, необходимый для приведения разнородных слагаемых в (2) к безразмерному виду. При этом следует гарантировать минимально допустимую степень эффективности реализации отдельных функций, которая определяется техническим заданием: . (3)
. (3) . (4)
. (4) (5)
(5) , (6)
, (6)
 – номер инвестора, а
– номер инвестора, а  – номер проекта. Ясно, что только одновременный анализ по всем четырем показателям может дать объективную оценку эффективности капиталовложений. Недостатком же существующих методик является отсутствие такого подхода [2,3]. Если каждый проект может быть выбран только одним инвестором и каждый инвестор выбирает только один проект, учитывая все четыре параметра эффективности, то нас интересует такой из них, который бы одновременно удовлетворял условиям:
– номер проекта. Ясно, что только одновременный анализ по всем четырем показателям может дать объективную оценку эффективности капиталовложений. Недостатком же существующих методик является отсутствие такого подхода [2,3]. Если каждый проект может быть выбран только одним инвестором и каждый инвестор выбирает только один проект, учитывая все четыре параметра эффективности, то нас интересует такой из них, который бы одновременно удовлетворял условиям: , (8)
, (8) , (9)
, (9) , (10)
, (10) , (11)
, (11) – матрица булевых переменных выбора,
– матрица булевых переменных выбора, ,
,  – ставка приведения доходной части j-го проекта для i-го инвестора. Кроме того, необходимо задать ограничения по строкам и столбцам матрицы X:
– ставка приведения доходной части j-го проекта для i-го инвестора. Кроме того, необходимо задать ограничения по строкам и столбцам матрицы X: ,
,  . (12)
. (12) , (13)
, (13) – вектор переменных;
– вектор переменных;  – вектор-функция критериев;
– вектор-функция критериев;  ,
,  – векторы-функции ограничений;
– векторы-функции ограничений;  – уровни ограничений. Причем,
– уровни ограничений. Причем, 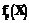 – вогнутые и
– вогнутые и  – выпуклые функции, а область допустимых решений не является пустым множеством:
– выпуклые функции, а область допустимых решений не является пустым множеством: .
. задач скалярной оптимизации (известными методами математического программирования):
задач скалярной оптимизации (известными методами математического программирования):  и
и  и найти
и найти  и
и  ,
,  .
. или
или  . (15)
. (15) – или
– или 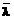 –задачу:
–задачу: или
или  .
. , оптимальную по Парето, в которой гарантируем результат:
, оптимальную по Парето, в которой гарантируем результат:
 .
.

 определяет s-критерий, значение которого необходимо улучшить.
определяет s-критерий, значение которого необходимо улучшить. ,
, ,
, ,
,
 ,
, , а координаты
, а координаты  и
и  найдены на шаге 1.
найдены на шаге 1. в установленных пределах и, если
в установленных пределах и, если  , строит
, строит  – или
– или  –задачу в форме:
–задачу в форме: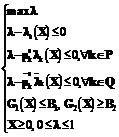 или
или  ,
, , где достигается результат:
, где достигается результат:
 .
. , то, выбрав точно так же
, то, выбрав точно так же  или
или  ,
, и
и 
 .
.