Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (midli@mail.ru) - , Ph.D | |
| Ключевое слово: |
|
| Page views: 11016 |
Print version Full issue in PDF (1.36Mb) |
При решении слабоструктурированной задачи, связанной с прогнозированием векторного слу- чайного процесса с использованием искусствен- ной нейронной сети (НС), возникают проблемы с выбором топологии сети, оптимизацией ее параметров и т.п. [1-3]. Принимая во внимание проблемы, связанные с использованием НС в задачах прогнозирования, остановимся на предлагаемых в данной статье методах их решения. Прежде всего, наиболее эффективный подход к решению задачи прогнозирования (экстраполяции) в нейросетевом логическом базисе заключается в том, что топология и алгоритмы оптимизации параметров сети разработаны на основе решаемой задачи, а не в результате «подгона» задачи под одну из стандартных парадигм. В статье предлагается архитектура специализированной многослойной НС и алгоритмы настройки ее структуры, предназначенные для прогнозирования и диагностики временных рядов произвольной природы. Структура экстраполятора. В соответствии с известными теоремами о полноте [1,4], а также с известным следствием [1] для построения экстраполятора выберем из них НС с одним скрытым слоем типа многослойного персептрона с сигмоидальными функциями активации нейронов как скрытого, так и выходного слоев сети. Предлагаемый экстраполятор представляет собой НС типа многослойного персептрона, охваченную обратной связью, которая реализует некоторую нелинейную зависимость вида
где xt – векторные значения процесса; d – так называемая глубина погружения. Данная модель может быть проиллюстрирована рисунком 1, где через Z-1 обозначен оператор задержки на один такт, то есть Z-1×xt = xt-1, а через НС – используемая (однослойная) НС с L нейронами скрытого слоя. К сожалению, упомянутая выше теорема о полноте и следствие из нее мало применимы в задачах экстраполяции рассматриваемых процессов: они не указывают оптимальное число нейронов L скрытого слоя. Неизвестным, вообще говоря, является и оптимальная глубина погружения d. Очевидно, структура используемой НС будет полностью определена только при задании L и d. Остановимся на этом подробнее. Запишем вначале выражения для определения прогнозируемых значений на 1,2, … тактов вперед:
Предполагается, что по данным обучающей выборки и при заданных L и d НС реализует функцию j(×) и позволяет реализовать соотношения (2). Очевидно, при t=d на основании (2) имеем
Выбирать значения глубины прогноза t больше, чем глубина погружения d, не имеет смысла, поскольку последующие предсказанные значения будут зависеть только от предыдущих, что делает такой прогноз весьма ненадежным. Таким образом, для d должно выполняться неравенство: d³dmin=t. (4) Покажем, что верхняя граница рассматриваемого параметра зависит от объема выборки экспериментальных данных, используемой для обучения сети и от количества нейронов L в ее скрытом слое. Вначале приведем известное [1] соотношение для рекомендуемого числа L:
где nc – число входов сети; mc – число ее выходов; N1 – объем обучающей выборки. В нашем случае mc = n, nc = n×d, (6) а значение N1 определяется следующим образом. Пусть исходные экспериментальные данные составляла выборка
а N – общее количество элементов вектора x. Первая строка таблицы обучающей выборки будет образована элементами векторов
N1=N'-d. (8) Подставляя теперь (8) и (6) в левую часть соотношения (5), получим
Физически наименьшее значение Lmin=1 (скрытый слой содержит только один нейрон), поэтому
Можно показать, что при фиксированном N' увеличение d приводит к уменьшению левой части последнего неравенства, поэтому его можно использовать для нахождения верхней границы глубины погружения dmax. Аналитическое решение (10) относительно d невозможно, численные же выкладки позволяют получить примерное значение для dmax:
где int{×} – функция выделения целой части числа. Таким образом, возможное значение для глубины погружения d удовлетворяет двойному неравенству
Возвращаясь теперь к выражению (5), найдем в нем наибольшее значение его правой части. Подстановка в нее (6) и (8) дает:
Учитывая, что в соответствии с (11) d<
откуда следует, что с ростом d правая часть (9) убывает и, таким образом,
Полученные неравенства (12) и (15) дают границы изменения значений параметров L и d, но не их оптимальные значения. Для получения этих оптимальных значений можно воспользоваться следующим подходом. Будем предполагать, что точность прогноза можно оценить, используя некоторую тестовую или контрольную выборку экспериментальных данных. Очевидно, средний квадрат ошибки прогноза для примеров этой выборки будет являться функцией как d, так и L, то есть E=E(d,L). При выборке в качестве критерия E(d,L) оптимальные значения dopt, Lopt являются решением оптимизационной задачи
Вид функциональной зависимости E(d,L), естественно, неизвестен, но можно полагать, что данная функция при ограничениях (12), (15) имеет только один минимум и может быть аппроксимирована квадратичной формой:
Коэффициенты b0¸b5 этой формы могут быть найдены следующим образом. В области возможных значений параметров d и L, определяемых (12), (15), проводится эксперимент, каждый i-й опыт которого заключается в создании, обучении и тестировании НС с заданными di, Li. Результатом (откликом) опыта является величина среднего квадрата Ei=E(di,Li). Очевидно, при числе таких опытов M, равном или большем шести, коэффициенты модели (17) определяются однозначно методом наименьших квадратов (МНК):
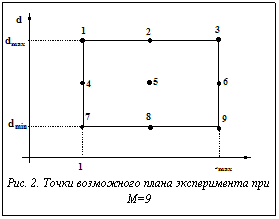
где Точки (di,Li) можно задавать по определенному плану. Пример плана такого эксперимента при M=9 приведен на рисунке 2. Значения d*, L*, минимизирующие выбранный критерий, находятся как решения системы уравнений
откуда получаем
Однако найденное решение (после округления) будет давать оптимальные (точнее, квазиоптимальные) значения
только в том случае, если d*, L* удовлетворяют неравенствам (12), (15). Если же одно (или оба) данных неравенства для найденных значений d*, L* не выполняются, точку (d*, L*), обеспечивающую минимум принятого критерия, следует искать на границе области определения d, L, то есть на границе прямоугольника, приведенного на рисунке 2, включая угловые точки прямоугольника. В этом случае нахождение dopt, Lopt сводится к достаточно тривиальной задаче одномерной оптимизации, на которой останавливаться не будем. Предложенный метод нахождения оптимальных значений параметров (dopt, Lopt) является приближенным, поскольку изложенная задача оптимизации относится к задачам дискретного программирования, и для поиска точных решений используются алгоритмы, учитывающие дискретный характер переменных d, L [5], например, динамическое программирование, метод ветвей и границ и др.
Предположим, что минимизируемая функция является функцией двух дискретных аргументов, то есть E=E(L, d), возможные значения которых на рисунке 3 отображены точками. Каким-либо образом (случайно или исходя из какой-то априорной информации) выбирается начальная точка, для которой определяется значение функции E(L0, d0). Затем находятся значения функции в четырех соседних точках Использование генетических алгоритмов [9,10]. Здесь каждый оптимизируемый параметр кодируется двоичным числом разрядности, достаточной, чтобы отобразить все возможные дискретные значения параметра. Совокупности таких чисел для всех параметров объединяются в одно двоичное слово, отображающее хромосому. Далее поиск минимума оптимизируемой функции проводится по известным [9,10] процедурам. Отметим, что генетические алгоритмы в действительности представляют собой, скорее, подход, чем единый алгоритм. Они часто требуют «содержательного наполнения» для решения рассматриваемой задачи. Чтобы рассчитывать на получение хорошего результата, необходимо учесть и предусмотреть большое количество факторов, таких как объем и структура популяции, отбор особей для выживания и/или скрещивания, обеспечение сходимости процедуры поиска, исключение нежелательных мутаций и т.д. С учетом сделанных выше замечаний генетический алгоритм был реализован в своем «классическом» варианте. Для оценки эффективности трех рассмотренных алгоритмов был проведен программный эксперимент. В результате выявлены и отмечены недостатки всех трех предлагаемых алгоритмов, самыми существенными из которых является факт «застревания» программы в точках локального минимума (для первых двух алгоритмов), невозможность полного исключения «нежелательных» мутаций и большие временные затраты на выполнение процедуры поиска (для третьего алгоритма). Предлагаемые алгоритмы оптимизации параметров эктраполятора на основе НС с обратной связью позволяют для разработанной специальной структуры сети осуществлять «оперативную» подстройку параметров сети на основе решаемой задачи, а не подгонять задачу под одну из стандартных структур. Проведенный программный эксперимент подтверждает эффективность такого промежуточного этапа оптимизации. Предложенная методика нахождения dopt, Lopt отражает наличие внешней обратной связи НС. Отметим, что оптимальные значения d и L взаимосвязаны друг с другом и не могут находиться с помощью соответствующих пакетных функций системы MATLAB. В процессе реализации машинного эксперимента автором была отработана недокументированная в известных источниках методика построения программных комплексов и GUI-приложений в среде MATLAB в сочетании с использованием имеющегося базового набора функций специализированных пакетов расширений. Список литературы 1. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Горячая линия – Телеком, 2001. 2. Дли М.И., Круглов В.В., Осокин М.В. Локально-аппроксимационные модели социально-экономических систем и процессов. - М.: Наука. Физматлит, 2000. 3. Дьяконов В.П., Абраменкова И.В., Круглов В.В. MATLAB 5.3.1 с пакетами расширений. - М.: Нолидж, 2001. 4. Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. - Новосибирск: Наука, 1996. 5. Корбут А.А., Филькельштейн Ю.Ю. Дискретное программирование. - М.: Наука, 1969. 6. Кузин Л.Т. Основы кибернетики. Т.1: Математические основы кибернетики. - М.: Энергия, 1972. 7. Коршунов Ю.М. Математические основы кибернетики. - М.: Энергоатомиздат, 1987. 8. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании. - М.: Финансы и статистика, 1999. 9. Курейчик В.М. Генетические алгоритмы. Обзор и состояние. // Новости искусственного интеллекта. - 1998. - №3. - С. 26-35. 10. Базы данных. Интеллектуальная обработка информации. / В.В. Корнеев, А.Ф. Гареев, С.В. Васютин, В.В. Райх. - М.: Нолидж, 2000. |
| Permanent link: http://swsys.ru/index.php?id=643&lang=en&page=article |
Print version Full issue in PDF (1.36Mb) |
| The article was published in issue no. № 2, 2003 |
Perhaps, you might be interested in the following articles of similar topics:
- Использование матричных квадродеревьев для хранения площадных картографических объектов
- Инструментальные и программные средства построения сетевых моделей
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
- Место XML-технологий в среде современных информационных технологий
Back to the list of articles
 , (1)
, (1) . (2)
. (2) , (5)
, (5) , где
, где , (7)
, (7) , а последняя – элементами векторов áxN-d, xN-d+1, xN'ñ.
, а последняя – элементами векторов áxN-d, xN-d+1, xN'ñ. Нетрудно видеть, что общее число обучающих примеров (равное числу строк таблицы обучающей выборки) равно при этом N'-d, то есть
Нетрудно видеть, что общее число обучающих примеров (равное числу строк таблицы обучающей выборки) равно при этом N'-d, то есть . (9)
. (9) . (10)
. (10) , (11)
, (11) . (12)
. (12) (13)
(13) , (14)
, (14) . (15)
. (15) . (16)
. (16) . (17)
. (17) , (18)
, (18) . (19)
. (19) ,
, . (20)
. (20) (21)
(21) Достоинства и недостатки (в основном громоздкость вычислений) этих методов хорошо известны [6,7]. Между тем, учитывая конкретные особенности рассмотренной задачи (два оптимизируемых параметра при небольшом числе возможных дискретных значений), можно предложить еще два, как представляется, достаточно перспективных алгоритма ее решения.
Достоинства и недостатки (в основном громоздкость вычислений) этих методов хорошо известны [6,7]. Между тем, учитывая конкретные особенности рассмотренной задачи (два оптимизируемых параметра при небольшом числе возможных дискретных значений), можно предложить еще два, как представляется, достаточно перспективных алгоритма ее решения.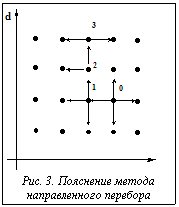 Метод направленного перебора. Данный метод является дискретным аналогом алгоритма Гаусса-Зайделя (другое название – метод покоординатного спуска) [8] (рис. 3).
Метод направленного перебора. Данный метод является дискретным аналогом алгоритма Гаусса-Зайделя (другое название – метод покоординатного спуска) [8] (рис. 3).
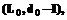
 , и выбирается точка, для которой значение меньше, чем в начальной – на рисунке 3 такой точкой принята точка 1 с координатами (L1,d1) = =(L0-1,d0). Далее повторяется «осмотр» точек, ближайших к точке 1 (ранее «осмотренные» точки пропускаются), осуществляется переход к следующей точке и так до тех пор, пока не найдется точка, для которой все соседние будут иметь большие значения минимизируемой функции.
, и выбирается точка, для которой значение меньше, чем в начальной – на рисунке 3 такой точкой принята точка 1 с координатами (L1,d1) = =(L0-1,d0). Далее повторяется «осмотр» точек, ближайших к точке 1 (ранее «осмотренные» точки пропускаются), осуществляется переход к следующей точке и так до тех пор, пока не найдется точка, для которой все соседние будут иметь большие значения минимизируемой функции.