Для реализации системного подхода к решению проблемы обеспечения информационной безопасности необходимо комплексное использование методов моделирования систем и процессов защиты информации [1]. Целями такого моделирования являются поиск оптимальных решений задач синтеза систем защиты информации (СЗИ), управления механизмами защиты, оценки эффективности использования средств и методов защиты и т.п.
Модель с позиций математического моделирования представляет логическое или математическое описание компонентов и функций, отображающих наиболее существенные свойства моделируемого объекта или процесса.
Моделирование системы заключается в построении некоторого ее математического аналога, адекватного с точностью до целей моделирования исследуемой системы, и выявления с помощью построенной модели необходимых свойств реальной системы.
 Исходной посылкой при разработке значительного числа моделей защищенных систем является очевидное предположение о возникновении некоторого ущерба в случае нарушения защищенности информации и необходимости расходования средств на обеспечение защиты данных. Полная ожидаемая стоимость финансовых потерь может быть выражена суммой расходов на защиту и потерь от ее нарушения (рис. 1).
Исходной посылкой при разработке значительного числа моделей защищенных систем является очевидное предположение о возникновении некоторого ущерба в случае нарушения защищенности информации и необходимости расходования средств на обеспечение защиты данных. Полная ожидаемая стоимость финансовых потерь может быть выражена суммой расходов на защиту и потерь от ее нарушения (рис. 1).
Очевидно, что оптимальным решением было бы выделение на защиту информации средств в размере Copt, поскольку именно при этом обеспечивается минимизация общих финансовых потерь.
Чтобы воспользоваться данным подходом к решению задачи, необходимо:
– знать или уметь определять ожидаемые потери при нарушении защищенности информации;
– уметь рассчитывать показатели, характеризующие зависимость между уровнем защищенности и финансами, затрачиваемыми на защиту информации.
Специалистами фирмы IBM [1] предложена следующая эмпирическая зависимость ожидаемых потерь от i-й угрозы информации:
Ri=10(Si+Vi-4),
где Si – коэффициент, характеризующий возможную частоту возникновения соответствующей i-й угрозы; Vi – коэффициент, характеризующий значение возможного ущерба при ее возникновении.
Суммарная стоимость потерь определяется формулой: R= .
.
Оценка ожидаемых потерь при нарушении защищенности информации принципиально может быть получена лишь тогда, когда речь идет о коммерческой тайне. Оценка уровня потерь при нарушении защищенности информации, содержащей государственную и военную тайну, в достаточно строгом виде до настоящего времени не получена [1].
Для определения уровня затрат, обеспечивающих требуемый уровень защищенности информации, необходимо знать: полный перечень угроз информации, потенциальную опасность проявления каждой из угроз, размеры затрат, необходимых для противодействия каждой из угроз.
В работе [2] представлен строго теоретический подход к моделированию систем защиты, основывающийся на посылке, что потенциально возможные проявления угроз и размеры потенциально возможного ущерба являются случайными событиями, поэтому они могут быть охарактеризованы законами распределения и типовыми характеристиками.
Основными положениями разработанной на основе указанного подхода динамической модели оценки потенциальных угроз являются следующие.
1. Понятие среднего коэффициента возможного проявления угрозы каждого типа – l, который рассматривается как случайная переменная с известным распределением вероятностей f(l).
2. Предположение, что количество проявлений угрозы rt в течение фиксированного периода времени зависит только от продолжительности периода наблюдения и среднего коэффициента проявления, в силу чего для числа проявления угроз справедливым признано распределение Пуассона:
P( =r/l)=
=r/l)= ,
,
где t – число периодов времени, за которое определены значения rt.
3. Представление распределения среднего коэффициента в виде гамма-распределения с параметрами, характеризующими эффективность защиты и определяемыми по рекуррентным зависимостям.
4. Получение безусловного распределения вероятностей числа проявлений угрозы за заданный период времени.
Оценка ожидаемого ущерба на основе описанной модели выполняется в следующей последовательности:
– рассматривается средний ущерб от проявления угроз и принимается нормальная функция его распределения;
– корректируются параметры распределения среднего ущерба по данным наблюдения за проявлениями угроз и размером имевшего место ущерба на нескольких интервалах времени различной продолжительности;
– строится окончательное распределение размера ожидаемого ущерба путем выделения неопределенных параметров из функции распределения вероятностей ущерба.
Однако в связи с тем, что необходимые фактические данные о проявлениях угроз и их последствиях практически отсутствуют, применение указанной модели и соответствующих методик весьма ограничено.
Учитывая сложность получения фактических данных о проявлениях угроз, представляется целесообразным с практической точки зрения использовать при построении модели защиты теоретико-эмпирический подход [1], основанный на синтезе основных положений эмпирического и теоретического подходов.
В этом случае на основе теоретико-вероятностных методов строятся модели, необходимые для определения и прогнозирования показателей защищенности, а на основе сбора и обработки статистических данных, полученных в ходе теоретических исследований и практических разработок вариантов защиты информации, формируются исходные данные, необходимые для практического использования моделей.
Рассмотрим метод оценки безопасности информации на основе теоретико-эмпирического подхода к моделированию СЗИ.
Пусть дана автоматизированная система (АС), базирующаяся на комплексе средств вычислительной техники в составе локальной вычислительной сети (ЛВС) ПЭВМ.
В АС используется СЗИ от несанкционированного доступа (НСД), представляющая собой аппаратно-программный комплекс.
СЗИ от НСД взаимодействуют с потоками случайных событий – попыток НСД, обусловленных действиями злоумышленников, неправильным распределением прав доступа, использованием несанкционированного программного обеспечения, ошибками в программно-технических комплексах идентификации и аутентификации и т.д.
Выполняя функции защиты от них, СЗИ производит обнаружение некоторой части попыток НСД, классифицирует их и обеспечивает необходимую реакцию с целью блокирования. Пропущенные запросы НСД поступают в информационную систему и могут нанести вред.
В соответствии с этим при выборе критериев качества СЗИ целесообразно исходить из анализа тех основных функций, для выполнения которых она предназначена:
– оперативное обнаружение попыток НСД с одновременной классификацией;
– оперативное противодействие НСД.
Процесс оперативного обнаружения НСД при условии идеальной надежности средств контроля может быть описан схемой принятия решения, представленной в таблице 1.
Таблица 1
|
Действительное событие
|
Решение, принятое СЗИ
|
Условное обозначение события
|
Вероятность события
|
Значения вероятности
|
|
НСД нет, А
НСД нет, А
НСД есть, 
НСД есть, 
|
НСД нет, В
НСД есть, В
НСД нет, 
НСД есть,
|
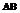



|
P1
P2
P3
P4
|
P1
P2
P3 =1- P4
P4
|
Здесь вероятности P1-P4 определяются вероятностями составляющих событий А и В по формулам Байеса.
По указанной схеме качество распознавания НСД можно характеризовать вероятностями P2 и P3 , которые соответствуют событиям  и
и  . Заметим, что вероятности P2 и P3 определяют методическую достоверность распознавания НСД: D = 1 – (P2 + P3).
. Заметим, что вероятности P2 и P3 определяют методическую достоверность распознавания НСД: D = 1 – (P2 + P3).
Таким образом, в качестве общей характеристики качества процесса обнаружения НСД можно использовать методические вероятности распознавания НСД PM(y), зависящие от свойств метода контроля y по обнаружению НСД.
Другой существенной характеристикой процесса обнаружения НСД является время обнаружения t0, которое может задаваться функцией распределения F(t) и основными моментами.
Преобразуем схему принятия решения с учетом характеристик надежности средств обнаружения НСД (табл. 2):
Заметим, что из-за отказов и сбоев в средствах защиты возможно появление ошибок P2* и P3*, причем возможен пропуск НСД, что увеличивает составляющую, обусловленную методической вероятностью пропуска НСД.
Таким образом, средства защиты осуществляют преобразование исходного потока НСД в потоки обнаруженных и пропущенных запросов НСД. Поток пропущенных НСД определяет P3* и вероятность обеспечения защиты.
Таблица 2
|
Действительное событие
|
Действительное состояние СЗИ
|
Принятое решение
|
Условное обозначение события
|
Значения вероятности
|
|
НСД нет, А
|
Исправна, С
|
НСД нет, В
|
А С В
|
P1
|
|
НСД нет, А
|
Исправна, С
|
НСД есть, 
|
А С 
|
P2
|
|
НСД есть, 
|
Исправна, С
|
НСД нет, В
|
 С В С В
|
P3 =1- P4
|
|
НСД есть, 
|
Исправна, С
|
НСД есть, 
|
 С С 
|
P4
|
|
НСД нет, А
|
Неисправна, 
|
НСД нет, В
|
А  В В
|
P 1*
|
|
НСД нет, А
|
Неисправна, 
|
НСД есть, 
|
А  
|
P2*
|
|
НСД есть, 
|
Неисправна, 
|
НСД нет, В
|
  В В
|
P3*
|
|
НСД есть, 
|
Неисправна, 
|
НСД есть, 
|
  
|
P4*
|
Под защищенностью АС от НСД будем понимать свойство, обусловленное возможностью противостоять несанкционированным воздействиям на программное обеспечение, информационные массивы или технические средства системы.
Свойство защищенности обусловлено, с одной стороны, закономерностями реализации угроз, а с другой – наличием в информационной системе средств защиты от НСД.
Защищенность АС от НСД может быть оценена следующими показателями:
– вероятностью защиты – Z(t);
– средним временем между пропущенными НСД – Тn;
– вероятностью пропуска определенного числа попыток НСД на интервале работы;
– средним числом пропущенных НСД на интервале времени работы;
– интенсивностью потока пропущенных НСД – h(t).
Вероятность обеспечения защиты означает вероятность отсутствия несанкционированных запросов к информации на выходе средств защиты и определяется следующим образом:

где  является функцией распределения случайной величины
является функцией распределения случайной величины  , которая представляет собой время между двумя соседними пропусками НСД.
, которая представляет собой время между двумя соседними пропусками НСД.
Вероятность обеспечения защиты и вероятность пропуска НСД связаны зависимостью:
F(t) = 1 – Z(t).
Функция Z(t) обладает следующими свойствами: 0 ≤ Z(t) ≤ 1, Z(0) = 0, Z(¥) = 0.
Среднее время между пропусками НСД:


где  – время между двумя последовательными пропусками ошибок;
– время между двумя последовательными пропусками ошибок;  – количество попыток НСД, пропущенных за время эксплуатации или испытаний.
– количество попыток НСД, пропущенных за время эксплуатации или испытаний.
Вероятность пропуска определенного числа попыток НСД на интервале работы (0,t):

где  – означает n-кратную свертку функции распределения F(t). Среднее число пропущенных попыток НСД определяется следующим образом:
– означает n-кратную свертку функции распределения F(t). Среднее число пропущенных попыток НСД определяется следующим образом:
 .
.
Соответственно, имеем интенсивность потока пропущенных попыток НСД:
 .
.
Аналогично [2] процесс возникновения попыток НСД в АС на основе ЛВС ПЭВМ можно описать неординарным случайным потоком с функцией распределения времени между соседними событиями потока

и функцией распределения числа НСД  .
.
Заметим, что информационные ресурсы, являющиеся объектом НСД, размещены на ЭВМ, входящих в ЛВС. Поэтому с целью упрощения модели будем рассматривать поток попыток НСД к одной из ЭВМ сети, учитывая влияние ЛВС наличием дополнительной угрозы доступа через сеть. Это обстоятельство позволяет считать, что моменты появления несанкционированных запросов образуют ординарный рекуррентный поток.
Как уже отмечалось, несанкционированные заявки на обслуживание возникают не только по причине действий злоумышленника, но и являются результатом ошибок программного обеспечения, неправильной настройки прав доступа, несоответствия условий эксплуатации СЗИ требованиям технических условий. В любом случае, независимо от первопричины возникновения заявки на НСД реализация ее определяется программно-технической средой вычислительной системы.
При этом обслуживание НСД-запроса приводит к выполнению некоторой последовательности команд ЭВМ. Учитывая случайность момента появления заявки, случайность состояния вычислительного процесса в этот момент и случайность возможных его состояний в последующие моменты времени, можно считать процесс обслуживания НСД-запроса также случайным.
Представим СЗИ в виде сетевой модели, состоящей из средств защиты Si (рис. 2). На вход средств защиты поступают потоки запросов НСД, определяемые моделью нарушителя на множестве потенциальных угроз {Ui}. Каждое из средств защиты отвечает за защиту от угрозы определенного типа и использует соответствующий защитный механизм. Его задача состоит в том, чтобы распознать угрозу и заблокировать несанкционированный запрос.
Действие системы защиты состоит в том, что исходный поток запросов разрежается, образуя выходной поток.
Обозначим входные потоки несанкционированных запросов Vi(t), i=1, ..., n, а потоки нераспознанных (пропущенных) системой защиты несанкционированных запросов  . Учтем факт неполного закрытия системой защиты всех возможных каналов проявления угроз отсутствием для m входных потоков средств защиты, что означает
. Учтем факт неполного закрытия системой защиты всех возможных каналов проявления угроз отсутствием для m входных потоков средств защиты, что означает  . Потоки запросов на НСД, поступающие по i-м каналам, разрежаются с вероятностями pi(y), которые зависят от используемого способа обнаружения и блокирования НСД.
. Потоки запросов на НСД, поступающие по i-м каналам, разрежаются с вероятностями pi(y), которые зависят от используемого способа обнаружения и блокирования НСД.
На выходе СЗИ образуется выходной поток, являющийся объединением выходных потоков i-x средств защиты и потока НСД-запросов, приходящих по m неконтролируемым каналам.
Обозначим через  функцию распределения времени между последовательно поступающими событиями потока, полученного вследствие применения к входящему потоку операции разрежения. Случайная величина tk, соответствующая интервалу времени между соседними событиями разреженного потока, может быть представлена как сумма случайного числа случайных слагаемых:
функцию распределения времени между последовательно поступающими событиями потока, полученного вследствие применения к входящему потоку операции разрежения. Случайная величина tk, соответствующая интервалу времени между соседними событиями разреженного потока, может быть представлена как сумма случайного числа случайных слагаемых:  , где х – случайное число.
, где х – случайное число.
Случайная величина x представляет собой число просуммированных интервалов в исходном потоке и распределена по закону Паскаля [3]:
P(x=k)=qpk-1, k=1,2,…; q=1-p; 0
С учетом этого выражение для F(t) можно записать в виде:

где  – функция распределения суммы независимых случайных величин с функцией распределения F(t); hk – длительность интервала времени между появлением (k) и (k-1) событий потока Vi(t).
– функция распределения суммы независимых случайных величин с функцией распределения F(t); hk – длительность интервала времени между появлением (k) и (k-1) событий потока Vi(t).
Обозначим через j(s) преобразование Лапласа плотности функции распределения F(t), то есть положим:
j(s)=  .
.
Для разреженного потока соответствую- щее преобразование Лапласа согласно [4] имеет вид:
 .
.
С учетом свойства независимости объединяемых потоков [4] плотность восстановления суммарного выходного потока определяется через плотности восстановления объединяемых потоков следующим образом:
 .
.
Преобразование Лапласа для плотности восстановления рекуррентного потока, полученного в результате разрежения некоторого другого потока, имеет вид [4]:  .
.
Если потоки стационарны, то:
 , где
, где  – математическое ожидание времени
– математическое ожидание времени  .
.
Тогда для суммарного потока можно записать:
 ,
,
поскольку для неконтролируемых потоков  .
.
Согласно теореме восстановления [5]:
 .
.
Отсюда для среднего времени между соседними пропусками попыток НСД запишем:
 ,
,
где Ti, Tj – средние времена между событиями i, j-х потоков НСД.
Определим случайную величину Yt как длину интервала времени от момента t до будущего момента пропуска НСД-запроса.
Обозначим через Fi(t) функцию распределения Yt i-го потока. Согласно [5] плотность распределения функции Fi(t) связана с функцией распределения Fi(t) следующей зависимостью:
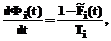
где  – функция распределения времени между последовательными пропущенными НСД-запросами на выходе i-го средства защиты; Ti – среднее время между пропусками НСД-запросов i-м средством защиты.
– функция распределения времени между последовательными пропущенными НСД-запросами на выходе i-го средства защиты; Ti – среднее время между пропусками НСД-запросов i-м средством защиты.
Учитывая определение для показателя защищенности, можно записать:
 , откуда:
, откуда:  .
.
Таким образом, если функция распределения Fi(t) имеет преобразование Лапласа, то можно получить выражения для  выходного потока, затем найти Fi(t), Få(t) и Zå(t).
выходного потока, затем найти Fi(t), Få(t) и Zå(t).
При большом числе составляющих потоков k, m оценку для показателя защищенности можно получить, используя предельные результаты и полагая, что суммарный поток стремится к пуассоновскому. В этом случае для оценки защищенности можно использовать формулу:
 .
.
Для случая исходных пуассоновских потоков эта формула является точной.
Таким образом, имеем выражение для показателя защищенности:  .
.
Рассмотрим далее вычисление моментов функции распределения числа пропущенных НСД-запросов. Преобразование Лапласа для функции восстановления рекуррентного потока имеет вид:  .
.
В случае стационарного рекуррентного потока:  .
.
В свою очередь, для разреженных потоков имеем:  ,
,  .
.
Для дисперсий можно записать:
 ,
,
 .
.
Поскольку исходные потоки являются независимыми, то функция восстановления суммарного выходного потока и дисперсия определяются следующим образом:
 ,
,
 .
.
Соответственно, для стационарных рекуррентных потоков имеем:
 ,
,
 .
.
Присутствующие в формулах вероятности пропуска НСД имеют реальное воплощение и являются характеристиками качества того или иного метода защиты. Основное влияние на значение указанной вероятности оказывают два фактора: методическая вероятность используемого способа защиты и вероятность работоспособности механизма защиты в момент совершения попытки НСД.
Список литературы
1. Семкин С.Н., Семкин А.Н. Основы информационной безопасности объектов обработки информации. - Орел, 2000.
2. Герасименко В.А., Малюк А.А. Основы защиты информации. -М.: Известия, 1997.
3. Беляев Ю.К. Предельные теоремы для редеющих потоков. - М.: Советское радио, 1967.
4. Кокс Д., Смит В. Теория восстановления. - М.: Советское радио, 1967.
5. Клейнрок Л., Теория массового обслуживания. - М.: Машиностроение, 1979.

 .
. =r/l)=
=r/l)= ,
,


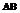



 и
и  . Заметим, что вероятности P2 и P3 определяют методическую достоверность распознавания НСД: D = 1 – (P2 + P3).
. Заметим, что вероятности P2 и P3 определяют методическую достоверность распознавания НСД: D = 1 – (P2 + P3).


 является функцией распределения случайной величины
является функцией распределения случайной величины  , которая представляет собой время между двумя соседними пропусками НСД.
, которая представляет собой время между двумя соседними пропусками НСД.

 – время между двумя последовательными пропусками ошибок;
– время между двумя последовательными пропусками ошибок;  – количество попыток НСД, пропущенных за время эксплуатации или испытаний.
– количество попыток НСД, пропущенных за время эксплуатации или испытаний.
 – означает n-кратную свертку функции распределения F(t). Среднее число пропущенных попыток НСД определяется следующим образом:
– означает n-кратную свертку функции распределения F(t). Среднее число пропущенных попыток НСД определяется следующим образом: .
. .
.
 .
. . Учтем факт неполного закрытия системой защиты всех возможных каналов проявления угроз отсутствием для m входных потоков средств защиты, что означает
. Учтем факт неполного закрытия системой защиты всех возможных каналов проявления угроз отсутствием для m входных потоков средств защиты, что означает  . Потоки запросов на НСД, поступающие по i-м каналам, разрежаются с вероятностями pi(y), которые зависят от используемого способа обнаружения и блокирования НСД.
. Потоки запросов на НСД, поступающие по i-м каналам, разрежаются с вероятностями pi(y), которые зависят от используемого способа обнаружения и блокирования НСД. функцию распределения времени между последовательно поступающими событиями потока, полученного вследствие применения к входящему потоку операции разрежения. Случайная величина tk, соответствующая интервалу времени между соседними событиями разреженного потока, может быть представлена как сумма случайного числа случайных слагаемых:
функцию распределения времени между последовательно поступающими событиями потока, полученного вследствие применения к входящему потоку операции разрежения. Случайная величина tk, соответствующая интервалу времени между соседними событиями разреженного потока, может быть представлена как сумма случайного числа случайных слагаемых:  , где х – случайное число.
, где х – случайное число.
 – функция распределения суммы независимых случайных величин с функцией распределения F(t); hk – длительность интервала времени между появлением (k) и (k-1) событий потока Vi(t).
– функция распределения суммы независимых случайных величин с функцией распределения F(t); hk – длительность интервала времени между появлением (k) и (k-1) событий потока Vi(t). .
. .
. .
. .
. , где
, где  – математическое ожидание времени
– математическое ожидание времени  .
. ,
, .
. .
. ,
,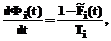
 – функция распределения времени между последовательными пропущенными НСД-запросами на выходе i-го средства защиты; Ti – среднее время между пропусками НСД-запросов i-м средством защиты.
– функция распределения времени между последовательными пропущенными НСД-запросами на выходе i-го средства защиты; Ti – среднее время между пропусками НСД-запросов i-м средством защиты. , откуда:
, откуда:  .
. выходного потока, затем найти Fi(t), Få(t) и Zå(t).
выходного потока, затем найти Fi(t), Få(t) и Zå(t). .
. .
. .
. .
. ,
,  .
. ,
, .
. ,
,  .
. ,
, .
.