Software & Systems

В настоящее время разработчикам многих программных систем приходится решать NP-трудные задачи. Существует множество алгоритмов решения таких задач, наиболее известный класс алгоритмов нахождения точного решения – методы ветвей и границ. Известно, что средняя их сложность – кубическая зависимость от размерности, а в качестве верхней границы – экспоненциальная [l,2].

В последнее десятилетие обнаружен эффект фазового перехода, когда при незначительном изменении параметров системы сложность решения точным алгоритмом возрастает па порядки [3], то есть приближается к верхней границе сложности. На примере задачи коммивояжера показано, что один из типов фазового перехода основывается на специфических топологических особенностях исходных данных [2,4], когда у весовой матрицы на главной диагонали находятся квадратные подматрицы, кластеры, элементы которых в среднем меньше элементов вне данных подматриц. Экспериментально получено, что сложность значительно возрастает при наличии строгого неравенства. Среднее число исследуемых ребер при поиске точного решения для матриц размером 20´20 и 30´30, сгенерированных по равномерному закону с учетом топологических особенностей, представлено в таблице 1. Количество статистических испытаний 100.

Наиболее сложным вариантом для решения точным методом является наличие кластеров, элементы которых строго меньше элементов вне данных диагональных подматриц. Несложный опыт позволяет определить, какие ребра наиболее часто используются при поиске точного решения. Проведено несколько сотен экспериментов для матриц размеров от 15 до 35 с представленными топологическими особенностями с целью выявления наиболее активно используемых ребер. Обобщенный график для случая, когда элементы в кластерах из интервала (0, 0.5), а вне кластеров – (0.5, 1), представлен на рисунке 1, при этом более 85% элементов, использованных при построении точного решения, принадлежат кластерам. Такое количество повторений комбинаций ребер из кластеров связано с особенностями работы метода ветвей и границ [5].

Дерево решения методом ветвей и границ бинарное. При построении дерева решения возврат происходит на предыдущую ветвь и производится проверка возможности существования решения на другой ветви. Если проверка показывает, что с оценкой на шаг вперед длина найденной части решения короче кратчайшего пути, известного на данном этапе построения решения, то исследуется вторая ветвь.

На основе представленных результатов можно отметить следующие недостатки классического алгоритма:

-         на каждом шаге учитывается длина решения на один шаг вперед,

-         нет элементов обучаемости,

-         максимальная сложность алгоритма пропорциональна экспоненте от размерности задачи,

-         степень использования элементов "малых" весов на тестовых матрицах значительно выше использования элементов "больших" весов. Причем при работе с матрицами исследуемой топологии число исследуемых элементов "малых" весов больше 85%.

Технология интеллектуального возврата предполагает наличие элементов обучаемости [6], когда возврат производится в область наиболее вероятного нахождения решения либо когда методами дополнительного анализа исключаются ветви, решение на которых не лучше найденного на данный момент, хотя оценка классическим методом ветвей и границ частичного решения показывает обратное.

При "строгих" кластерах входящие в них узлы с большой вероятностью последовательно включаются в точное решение, а узлы из подматриц перехода соединяют эти частные решения. На основе этого предлагается алгоритм интеллектуального возврата, который внутри кластеров находит точное решение, затем методом ветвей и границ выбирает элементы из подматриц перехода, при этом возникает проблема объединения частичных гамильтоновых циклов в один гамильтонов цикл. Рассматриваются два подхода к решению данной проблемы.

Введем некоторые обозначения: wk, – k-я весовая подматрица; Lk – длина пути внутри кластера k; рk = [а1, ..., as] – путь внутри кластера k размером s; ink, outk – точки входа и выхода из кластера.

Подход 1. После вычисления точки входа и точки выхода необходимо скорректировать путь внутри кластера с минимальными погрешностями. При данном подходе предполагается, что ink ¹ outk. Ситуация равенства рассматривается как ошибочная.

Введем дополнительные обозначения для элементов оптимального пути внутри кластера, здесь prev(x) = у означает, что в оптимальном решении рk х следует за y; next(x) = у означает, что в оптимальном решении рk у следует за х.

Так как вычисленный точным методом путь внутри кластера замкнут, то в качестве первого элемента можно выбрать любой элемент из рk, поэтому в качестве такового выберем ink: a1 = ink, а элементу outk присвоим номер х, то есть аx = outk.

Соединение будем делать по принципу построения нового пути Р2k = [b1,..., bs], в котором b1 = ink, bs = outk.

Метод 1.1.

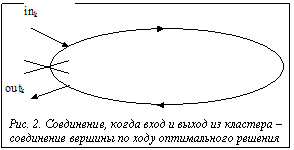
Если Prev(ink) == outk, тогда bi = аi "i Î [1 .. s] и длина пути Lnew = Lk - wk(outk, ink) (рис. 2),

иначе

Метод 1.2.

B2=Next(outk),bi=Next(bi-1), "i Î [3,s-x+2].

Введем дополнительное обозначение с = card[3, s - х + 2], определяющее количество целых чисел в заданном интервале.

Bc+3 = Next(ink), bi = Next(bi-1), "i = [с + 4, s].

Длина пути изменяется следующим образом:

Lnew = Lk - wk(Prev(ink), ink) - wk(ink, Next(ink)) - - wk(outk, Next(outk)) + wk(Prev(ink), Next(ink)) + + wk(ink, Next(outk) (рис. 3.)

В данном подходе метод 1.1 дает точное решение внутри кластера, метод 1.2 – приближенное. Если максимальный элемент кластера обозначить kmax, a минимальный kmin, то максимальная погрешность на данном кластере составляет:

emax=(kmfx-kmin)*2.

Подход 2. Данный подход заключается в более точном вычислении пути и более гибкой работе с кластерами и позволяет учитывать возможность не однократного входа-выхода из полученного кластера, а многократную последовательность входов-выходов.

Основной отличительной чертой данного алгоритма является то, что нет необходимости пересчитывать путь внутри кластера. Если полученные элементы входа и выхода соответствуют методу 1.2, то следует применить метод 2.1, который заключается в следующем.

Метод 2.1. После определения входа и выхода необходимо вычислить путь по кластеру и вес пути. Если условия соответствуют методу 1.1, то вычисления проводятся в соответствии с ним, иначе

Р2k = [b1, ..., bx], в котором b1 = ink, bx = outk.

Строится последовательность:

bi=Next(bi-1)," iÎe[2,x].

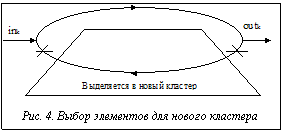
Элементы, которые не вошли в путь по кластеру, обозначим [с1, ..., cs-x] и выделим в кластер, который будет рассматриваться отдельно. Для него необходимо посчитать минимальный путь.

Длина соответствует длине выбранного участка Р2k (рис. 4).

Данный подход позволяет учитывать особенности матриц и получать в среднем более точные решения по сравнению с подходом 1 на матрицах, у которых в кластерах элементы строго меньше элементов вне кластеров. Обеспечивается снижение количества элементов малых весов, используемых при построении решения, по сравнению с классическим механизмом возврата. Данный подход основывается на гипотезе, заключающейся в том, что при выделении из кластера подматрицы, которая содержит часть оптимального пути по кластеру, и фиксацией точек входа и выхода, данная часть пути будет оптимальна и в полученной подматрице.

Алгоритм интеллектуального возврата реализует поиск оптимального пути в подматрицах перехода с учетом выбранного подхода к соединению внутри кластеров и учета длины пути в неиспользованных в частичном решении диагональных подматриц.

1. ПРОЦЕДУРА “НАЙТИ РЕШЕНИЕ”

1.1. Выделить кластеры.

1.2. Вычислить путь внутри кластеров.

1.3. Найти приближенное решение задачи алгоритмом k-оптимизации [7].

1.4. В подматрицах перехода создать списки элементов из интервала (0, "длина приближенного решения" – "сумма длин решений из подматриц перехода").

1.5. Упорядочить списки в подматрицах перехода по возрастанию.

1.6. В качестве первого кластера выбрать кластер, у которого минимальный элемент подматриц перехода выхода максимален.

1.7. Создать список L номеров неиспользованных кластеров, номер первого кластера присвоить переменной ПЕРВЫЙ, если поиск решения по "подходу 1", то удалить из L первый кластер.

1.8. Вызвать процедуру “ИССЛЕДОВАТЬ” (номер предыдущего кластера).

2. ПРОЦЕДУРА “ИССЛЕДОВАТЬ” (номер предыдущего кластера).

2.1. Если список L пуст.

2.1.1. Выбрать из подматрицы перехода из "номер предыдущего кластера" в ПЕРВЫЙ элемент, замыкающий гамильтонов цикл.

2.1.2. Если длина решения меньше текущего, то записать новое решение.

2.2. Иначе.

2.2.1. Номерам наименьших элементов присвоить нулевое значение.

2.2.2. Выбрать элемент из подматриц перехода, номера которых принадлежат L, следующий наименьший.

2.2.3. Внести его как out для "номер предыдущего кластера".

2.2.4. Вычислить текущую длину пути, вычислить оценку неиспользованных кластеров, вычислить нижнюю границу для подматриц перехода. Если длина частичного решения меньше текущего, то

2.2.4.1. Если использовался "подход 2", то создать новый кластер и внести его в список L.

2.2.4.2. ИССЛЕДОВАТЬ (номер нового кластера).

2.2.4.3. Если использовался "подход 2", то удалить внесенный кластер из списка L.

2.2.5. Перейти к 2.2.2.

Предварительные оценки точности решения для подхода 1 представлены в таблице 2 для различных размеров кластеров. Количество экспериментов равно 100. Если заявлен размер кластеров 5´5 на матрице размером 20´20, это означает, что в ней четыре кластера данного размера. Представлен вариант строгой кластеризации, когда элементы в диагональных подматрицах строго меньше элементов вне данных подматриц. В случае кластеризации, когда строгое неравенство верно для средних значений, погрешности предложенных подходов значительно возрастают. Алгоритм интеллектуального возврата обозначен в таблице мнемоническим названием BBmod, метод ветвей и границ – ВВ. Алгоритмы реализованы на SUN Java 2.

Таблица 2 

Результаты тестирования алгоритма интеллектуального возврата

Максимальная полученная погрешность порядка 14%, в то время как точность приближенных алгоритмов колеблется от 50% до 100% [7,8]. При этом среднее время решения точным алгоритмом возрастает экспоненциально, в то время как алгоритм интеллектуального возврата в среднем показывает полиномиальную зависимость от размерности и от количества кластеров; у тестируемого алгоритма в данной реализации существует статическая задержка на вычисления порядка 500 мсек на каждый кластер, что связано с особенностями реализации. Теоретически точность и сложность алгоритма при использовании подхода 2 должны быть выше, что является предметом дальнейших исследований.

Как видно из представленных результатов, предлагаемые подходы позволяют использовать фазовый переход для разработки алгоритмов интеллектуального возврата, которые превосходят по точности существующие приближенные алгоритмы и позволяют совместить в себе механизмы, используемые в точных алгоритмах поиска решения, и constraint-технологию.

Список литературы

1. CP-AI-OR'99, Workshop on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems - Ferrara, Italy, 25 - 26 February, 1999.

2. Valkovsky V.B., Gerasimov M.B., Sawin K.О. Phase Transitions in TSP and Matrix Topology. In Proc. of the Joint Workshop on Integration of AI and OR techniques in Constraint Programming for Combinatorial Optimization Problems. Universita degli Studi di Ferrara - Facolta di Ingegneria, Italy 1999. 5 pp.

3. Gent I., Walsh T. "The TSP Phase Transition", Research Report/95/178, Department of Computer Science, University of Stralhclyde.

4. Вальковский В.Б., Беляев С.А. Использование фазовых переходов при решении комбинаторных задач. // Программные продукты и системы. - 2000. - №4. - с. 37-38.

5. Пападимитриу X., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. - М.: Мир, 1985.

6. Baker A.B., Intelligent Backtracking on Ihe Hardest Constraint Problems, Computational Intelligence Research Laboratory and Department of Computer and Information Science, 1269 University of Oregon, February 6, 1995.

7. Lower E., Lenstra J., Rinooy A. Kan, Shmoys D. "The Travelling Salesman Problem".

8. Frieze A.M., Galbiati G., Maffioli F. "On the Worst-Case Performance of Some Algorithms for the Asymmetric Travelling Salesman Problem".