 Прогнозирование нестационарных случайных процессов является актуальной задачей в современной математической экономике [1]. Информация о будущих значениях цен на товары, котировках акций или курсе национальной денежной единицы во многом способствует выработке оптимальной модели поведения экономического субъекта на рынке. Существующие методы, реализованные в пакетах программ обработки статистической информации и описанные в литературе [2,3], ориентированы в основном на ряды, в которых присутствует случайная компонента, вызывающая колебания цены около своего тренда. В этом случае применение авторегрессионных методов или методов скользящего среднего бывает достаточно для получения достоверного прогноза, но при возникновении скачков цены, вызванных внешними факторами, необходимо применять методы, ориентированные на прогнозирование в условиях нестационарности. В статье приводится метод и алгоритм прогнозирования цены, основывающийся на минимизации апостериорного риска с заданной функцией потерь и на накопленной статистике изменения значений цены.
Прогнозирование нестационарных случайных процессов является актуальной задачей в современной математической экономике [1]. Информация о будущих значениях цен на товары, котировках акций или курсе национальной денежной единицы во многом способствует выработке оптимальной модели поведения экономического субъекта на рынке. Существующие методы, реализованные в пакетах программ обработки статистической информации и описанные в литературе [2,3], ориентированы в основном на ряды, в которых присутствует случайная компонента, вызывающая колебания цены около своего тренда. В этом случае применение авторегрессионных методов или методов скользящего среднего бывает достаточно для получения достоверного прогноза, но при возникновении скачков цены, вызванных внешними факторами, необходимо применять методы, ориентированные на прогнозирование в условиях нестационарности. В статье приводится метод и алгоритм прогнозирования цены, основывающийся на минимизации апостериорного риска с заданной функцией потерь и на накопленной статистике изменения значений цены.
Метод минимизации апостериорного риска
Рассмотрим динамическую модель ценообразования, описываемую стохастическим дифференциальным уравнением
 , (1)
, (1)
где f(t,p(t)) и F(t,p(t)) – коэффициенты сноса и диффузии [4]; n(Dt,A) – случайная пуассоновская мера с параметром l(t); v – случайная величина, вызывающая случайное скачкообразное приращение цены с(v) согласно закону Р(c(v)) в моменты времени tk с экспоненциальным законом распределения. Будем далее исходить из закона Р(с(v)) = d(v – a), a > 0, полагая, что цена есть возрастающий процесс. В математическом плане такая модель подтверждается известным [5] утверждением, что всякий стохастически непрерывный процесс с независимыми приращениями можно представить суммой независимых пуассоновских и винеровских процессов. Любая реализация цены есть решение уравнения (1) и имеет общий вид
 (2)
(2)
где интеграл от пуассоновской меры
 (3)
(3)
и 
Интеграл (3) представляет собой скачкообразное изменение цены в случайные моменты времени t1,..., tk. Видно, что со случайным изменением амплитуд скачков c(vk) решение (2) представимо в виде
 (4)
(4)
и составляет реализацию случайного процесса. Поэтому для вычисления прогнозных значений необходимо воспользоваться законом распределения этого процесса, либо его первыми моментами как числовыми характеристиками. Однако такой подход будет неполным, так как прогнозирование связано с ошибками, для учета которых целесообразно воспользоваться характеристикой риска принятия прогнозного решения. В качестве такого риска, как критерия качества прогнозирования, примем условный апостериорный риск, накопленный к текущему моменту времени. Его выражение запишем в виде
 , (5)
, (5)
где L(t,pt,pt*) – ограниченная функция потерь. Процесс р(t) определяется распределением вероятности w(pt,t;pt,t) перехода в состояние (р(t),t) из состояния (р(t),t), t £ t. Это распределение находится из обратного уравнения Колмогорова, записываемого с учетом уравнения (1) в виде
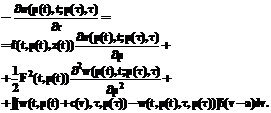 (6)
(6)
Очевидно, решение относительно прогнозного значения цены следует отыскивать путем минимизации критерия (5) на множестве допустимых решений D
S(w(pt,t;pt,t),t,pt))= . (7)
. (7)
В результате преобразований (7) с учетом (6) получим дифференциальное уравнение для S(w(pt,t;pt,t),t,p*(t)) и последующего вычисления прогнозного значения цены:
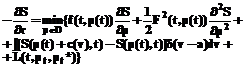 (8)
(8)
с граничным условием S(w,p(T),T)=0.
Для практической реализации метода необходимо восстановить функции f(t,p(t)) и F(t,p(t)). При этом f(t,p(t)) = T¢t(t,ptr(tk)), где T(t,ptr(tk)) – тренд цены, полученный методом наименьших квадратов на основе статистики ptr(tk) при исключении из исходных данных значений скачков. Функция F(t,p(t)) восстанавливается методом наименьших квадратов по значениям
 .
.
Пусть задан критериальный функционал (5) с квадратичной функцией потерь L(t,p(t),p*(t)) = (p-p*)2. Для получения аналитического выражения для р* произведем следующие действия. Разложим функции f(t,p(t)) и F(t,p(t)) в ряды Тейлора до линейного члена и обозначим
 (9)
(9)
Продифференцируем правую часть (8) по р* и приравняем результат к 0:
 , получаем оптимальную цену р* как функцию переменных S и p.
, получаем оптимальную цену р* как функцию переменных S и p.
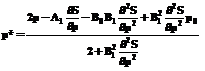 . (10)
. (10)
Подставляем это выражение в (8) для получения дифференциального уравнения для S(t,p(t)):
 (11)
(11)
Представляем S(t,p(t)) в виде ряда по степеням р(t) с неизвестными коэффициентами hi(t). Ограничимся тремя слагаемыми
 . (12)
. (12)
Подставляем (12) в (11) и, приравняв коэффициенты при одинаковых степенях p(t), составляем систему обыкновенных дифференциальных уравнений для hi(t).


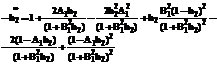 (13)
(13)
с граничными условиями h0(Т)=0, h1(Т)=0, h2(Т)=0.
Здесь 

 .
.
Решив систему уравнений (13), определяем вид функции (12). Задавшись допустимым уровнем потерь S³0 в момент времени T+1, решим уравнение (12) относительно прогнозного значения p(T+1), обеспечивающего заданный уровень потерь в заданный момент времени.
Структура алгоритма прогнозирования цены
1. Восстанавливаются функции f(t,p(t)), F(t,p(t)). Устанавливается степень S(p(t),t) в представле- нии (12).
2. Решить (численным методом) систему уравнений (13).
3. Задать для момента времени T+1, на который строится прогноз значения цены, требуемый уровень минимума средних потерь S(T+1, p(T+1)) ³ 0.
4. Решить уравнение (12) относительно значения цены рT+1*, обеспечивающей в момент времени (T+1) требуемое значение средних потерь.
Анализ алгоритма и выводы
Предложенные метод и алгоритм прогнозирования цены на основе минимизации апостериорного риска обладает рядом преимуществ по сравнению со стандартными авторегрессионными методами:
1) математическая модель учитывает характер и специфику прогнозируемого процесса;
2) метод ориентирован на прогнозирование нестационарных случайных процессов за счет добавления в правой части (1) третьего слагаемого;
3) прогнозируемые значения цены являются оптимальными в смысле минимизации функциона- ла (5), формируемого лицом, принимающим решения.
При реализации метода следует учесть, что более высокий порядок полинома (12) увеличивает размерность системы (13). При этом ее решение относительно hi(t) и решение уравнения (12) относительно прогнозного значения цены становится нетривиальным и требует собственной алгоритмической реализации.
Проанализировав результаты, отметим, что изложенный метод является расширением набора инструментов для прогнозирования значений случайных временных рядов, в том числе и нестационарных.
Список литературы
1. Малыхин В.И. Финансовая математика. – М.: ЮНИТИ, 1999.
2. Клеменс М.П. Хендри Д.Ф. Прогнозирование в макроэкономике. // Обозрение прикладной и промышленной математики.–1996. - Т. 3. - Вып. 6.
3. Тюрин Ю.Н. Макаров А.А. Статистический анализ данных на компьютере. – М.: Финансы и статистика, 1995.
4. Гнеденко Б.В. Курс теории вероятностей – М.: Наука, 1961.
5. Гихман И.И. Скороход А.В. Введение в теорию случайных процессов.–М.: Наука, 1965.

 , (1)
, (1) (2)
(2) (3)
(3)
 (4)
(4) , (5)
, (5)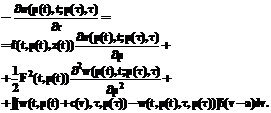 (6)
(6) . (7)
. (7)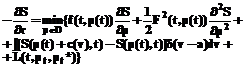 (8)
(8) .
. (9)
(9) , получаем оптимальную цену р* как функцию переменных S и p.
, получаем оптимальную цену р* как функцию переменных S и p.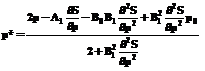 . (10)
. (10) (11)
(11) . (12)
. (12)

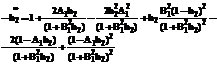 (13)
(13)

 .
.