Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: B.K. Lebedev (lebedev.b.k@gmail.com) - Institute of Computer Technology and Information Security, Southern Federal University (Professor), Taganrog, Russia, Ph.D | |
| Ключевое слово: |
|
| Page views: 17202 |
Print version Full issue in PDF (1.30Mb) |
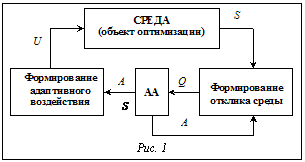
Методы поисковой адаптации на основе механизмов генетики являются эффективным средством решения оптимизационных задач [1-4], преимущество которых в параллельной обработке множества альтернативных решений, что является мощным средством выхода из локальных оптимумов. Генетические алгоритмы (ГА) – алгоритмы случайного поиска, однако заложенная в них стратегия эволюционного развития на основе естественного отбора приводит к синтезу решений, близких к оптимальным [5]. Тем не менее эффективность ГА во многом определяется как учетом специфики решаемой задачи, так и использованием новых и модифицированных процедур поиска. Специфика решаемой задачи прежде всего учитывается при разработке структуры, принципов кодирования и декодирования хромосом. При разработке ГА руководствуются следующими соображениями [6]. Желательно, чтобы хромосомы в разрабатываемых алгоритмах были гомологичными, что исключает возникновение нелегальных решений и упрощает выполнение генетических операторов, модифицирующих хромосомы. Достоинством ГА является линейная оценка временной и пространственной сложности генетических процедур, выполняемых на каждой итерации, что дает возможность решать задачи большой возможности, а это важно при проектировании СБИС. Для повышения эффективности в генетических алгоритмах используются структурирование хромосом и многохромосомные представления решения. Каждая часть структурированной хромосомы или каждая хромосома в случае многохромосомных представлений отвечает за определенный аспект решения. Это упрощает и делает более целенаправленным процесс генетического поиска. Степень изменения решения зависит как от способа кодирования хромосом, так и от способа выполнения генетических операторов (кроссинговер, мутация). В алгоритмах, предложенных в [6], используются методики чередования типов хромосом одного решения и типов генетических операторов, причем на первых итерациях степень изменения решения более значительна, чем при последующих. Один из приемов повышения эффективности ГА связан с распараллеливанием ГА с последующей миграцией хромосом из подпопуляций. Это связано с увеличением пространственной и временной сложности. Автором предложен метод формирования виртуального набора популяций, что позволяет организовать распараллеливание процесса поиска без увеличения временной и пространственной сложности [6]. Отличительной чертой метода является то, что процесс декодирования хромосомы Hj, принадлежащей исходной популяции генотипов П={Hj| j=1,2,…,M}, опирается на вектор Bi. Таким образом, одному и тому же генотипу Hj в зависимости от вида Bi соответствуют различные фенотипы. Виртуальный набор популяций V={, i=1,2,..,l} определяется набором векторов B={Bi| i=1,2,…,n} при заданном наборе генотипов П. Пара определяет одну популяцию vlÎV. Задается базовый вектор B*. Между В* и каждым из векторов BiÎB установлено взаимнооднозначное соответствие Г(B*,Cl,Bl). Декодирование генотипа Hj осуществляется с использованием вектора В*, и строится фенотип Р*. Затем с помощью соответствий по P* строятся фенотипы, принадлежащие различным популяциям. При использовании виртуального множества популяций для каждого фенотипа, соответствующего генотипу Hj и вектору Bl, рассчитывается целевая функция (ЦФ) Fjl. Таким образом, одному генотипу Hj соответствует множество оценок Fj={Fjl | l=1,2,…,nl}. Среди оценок множества Fj выбирается Фj с максимальным значением ("l)[Фj³Fjl]. Эта оценка и будет ЦФ генотипа (хромосомы) Hj. Алгоритмы селекции как при выборе родительских пар для скрещивания, так и при редукции расширенной популяции генотипов (хромосом) ПR до размеров исходной популяции Пn опираются на оценку Фj. Использование виртуального множества популяций на одном наборе генотипов позволяет произвести распараллеливание генетического поиска, практически не изменяя пространственной и временной сложности алгоритма. Наблюдение за живыми организмами показывает, что адаптация, являющаяся движущей силой эволюционного развития, многолика и проявляется как сочетание генетической адаптации и адаптации на основе самообучения и самоорганизации [7-9]. В работах [9-11] процесс оптимизации рассматривается как адаптивный поисковый процесс на основе самообучения и самоорганизации, моделируемый вероятностными обучающимися автоматами адаптации (АА) [12]. В 1948 г. У. Эшби предложил аналоговое электромеханическое устройство гомеостат, моделирующее свойство живых организмов поддерживать некоторые свои характеристики (температуру тела, содержание кислорода в крови и т.д.) Гомеостат Эшби представляет собой динамическую систему dU/dt = F(U,X,E). Состояние системы описывается вектором U=(u1,u2,…,un) и определя- ется как вектором управляемых параметров Y={x1,x2,…,xm}, так и вектором неуправляемых параметров, характеризующих стохастические свойства среды. Изменение состояния U гомеостата осуществляется с помощью управляющего воздействия на параметры Х, причем целью управления является выведение гомеостата в заданное состояние U*, то есть минимизация показателя Q=|U- U*|. Процесс выведения гомеостата в заданное состояние производится методом проб и ошибок, который фактически сводится к случайному перебору управляющих воздействий на Х с последующей проверкой их эффективности и реакции. При этом возможны два вида реакции. Отрицательная реакция R- возникает в ответ на управляющее воздействие, не приводящее к уменьшению показателя Q. Эта реакция в соответствии с алгоритмом гомеостата вызывает выбор очередного случайного воздействия. Положительная реакция R+ следует при уменьшении показателя Q. Она вызывает повторение воздействия, приведшего к положительному результату. Поведение гомеостата целесообразно и направлено на поиск и сохранение в системе состояния, которое обеспечивает положительную реакцию R+. Значительным шагом в развитии технических устройств для имитации адаптации М.Л. Цетлиным был предложен подход, основанный на использовании вероятностных обучающихся автоматов [12]. Представим работу гомеостата как функционирование некоторого вероятностного автомата, действующего в случайной среде. Тогда гомеостат распадается на два компонента – среду и управляющее устройство. Под средой понимается объект управления (объект оптимизации), а управляющее устройство работает в соответствии с алгоритмом случайного поиска. Основываясь на этой идее, Цетлин поместил в среду, характеризующуюся случайной реакцией, вероятностный АА для реализации функции управляющего устройства. Адаптация автомата производится путем самообучения в процессе его функционирования. На каждом такте работы адаптивной системы в соответствии со значениями А выхода АА формируется управляющее воздействие U, приводящее к изменению состояния среды S и показателя F(S) (рис.1). Q является откликом среды на реализацию управляющего воздействия. Под действием Q автомат переходит в новое состояние и вырабатывает новые выходные значения А. Пусть P={Si | i=1,2,…} – пространство возможных состояний (решений задачи разбиения). Цетлин предложил структуру и механизм поведения автоматов, адаптирующихся к среде, и впервые формализовал эту проблему [12]. АА способен воспринимать два входных сигнала: поощрения при удаче (+) и наказания при неудаче (-). Под действием этих сигналов осуществляется переход АА в новые состояния. В зависимости от состояния АА на его выходе может быть один из выходных сигналов А1,…,Аn, соответствующий альтернативной структуре или действию, число которых не должно быть большим n=2¸5. Задача адаптации состоит в том, чтобы поддерживать в объекте ту структуру, которая обеспечивает максимальную эффективность объекта при соблюдении заданных ограничений и иметь возможность переходить на другую альтернативную структуру, если в результате изменения условий она окажется лучше. АА как конечный вероятностный автомат определяется следующей пятеркой: ({S}, {I}, {A}, Ф, f). S(t+1) = Ф(S(t)), I(t+1); A(t) = f(S(t)). Здесь S(t) – внутреннее состояние автомата в момент t; I(t) – вход автомата (отклик среды – сигнал поощрения или наказания); Ф – функция перехода из состояния в состояние, Ф:{S}´{I}®{S}; A(t) – выход автомата в момент времени t, то есть его альтернатива (стратегия); f – функция выхода, f: {S}®{A}. Характеристикой среды является вектор, имеющий n компонентов: С=(Р1,Р2,…,Рn). При этом Рi есть вероятность того, что за действия или структуру Аi АА получит от среды сигнал поощрения, а с вероятностью Qi = (1-Рi) – наказания. Подчеркнем, что хотя Рi объективно существуют, автомату они априорно неизвестны. Если бы это было не так, то задача адаптации решалась бы тривиально. Рассмотрим примеры алгоритмов альтернативной адаптации для случая, когда имеются лишь две допустимые альтернативы (n=2) [9,10].
Автомат с обучением (рис. 3) имеет параметр Р, характеризующий вероятность условного перехода на графе АА. Величина этой вероятности равна вероятности того, что первая альтернатива лучше второй. Эту вероятность легко оценить на базе предыстории работы алгоритма (а вначале можно выбрать Р=1/2). По сигналу наказания автомат переходит в состояние Z, из которого сразу же возвращается либо в состояние А1 с вероятностью Р, либо в состояние А2 с вероятностью 1-Р. Прежде всего, случайным образом или по результатам работы какого-либо алгоритма реализуется начальная альтернатива. В последующем на каждом шаге (итерации) работа адаптивного алгоритма выполняется за четыре такта: 1) осуществляется расчет параметров P среды и объекта адаптации (ОА) после реализации ранее выбранной альтернативы; 2) по параметрам Р оценивается состояние ОА в среде и на основании этого вырабатывается управляющий сигнал поощрения или наказания; 3) под действием управляющего сигнала АА переходит в новое состояние; 4) на четвертом такте реализуется альтернатива, соответствующая состоянию АА. Существует большое число алгоритмов адаптации [10-13], и выбор одного из них зависит от специфики решаемой задачи. Поэтому правильный выбор алгоритма адаптации в значительной степени определяет успех создаваемой адаптивной системы. Все многообразие АА, в первую очередь, определяется механизмами переходов: внутри группы состояний, соответствующих одной альтернативе, и между группами состояний, то есть переход к новым альтернативам. Другой важной проблемой является методика выработки управляющих сигналов (поощрения или наказания) при анализе состояния ОА в среде. Как указывалось выше, процесс поисковой адаптации имеет последовательный многошаговый характер. В связи с этим важное значение имеет алгоритм, определяющий последовательность и тип процедур, выполняющихся на каждом из многократно повторяющихся шагов (итераций). Адаптация на основе самообучения и самоорганизации доминирует в процессе существования и развития конкретного живого организма, в том числе и человека. ОА является конкретный индивидуум. Генетическая адаптация является средством развития организма как вида, и ее механизмы реализуются на множестве организмов (популяции) как на едином целом. Общий подход к построению поисковых адаптивных процедур опирается на сочетание принципов адаптации на основе самообучения, самоорганизации и генетического поиска.
При генетическом поиске просматривается множество решений, “разбросанных”, особенно в начале поиска, по всему пространству решений. Однако в процессе генетического поиска решения с худшими оценками по сравнению с другими, лежащими в областях, включающих точки с глобальным оптимумом, могут быть потеряны. Другая проблема генетического поиска заключается в том, что решения, содержащиеся в развивающейся популяции, бывают очень близки к оптимальным, но механизмы генетического поиска, реализующие случайные изменения, часто не находят ту цепочку изменений, которые приводят к оптимальному решению. Для этого нужны “осмысленные” изменения, направленные в сторону глобального оптимума. Такие свойства как раз присущи адаптивным поисковым процедурам на основе самообучения и самоорганизации. В связи с этим для преодоления барьера локальных оптимумов обоснованным является подход, основанный на сочетании генетического поиска с адаптацией на основе самообучения и самоорганизации. Простейшим способом сочетания генетического и адаптивного обучающегося алгоритма является их последовательная реализация. После отработки ГА в популяции, полученной на последней генерации, отбирается несколько решений (может быть, одно лучшее), затем подключается адаптивный обучающийся алгоритм, использующий отобранные решения в качестве начальных.
Массив задача включает все исходные данные. Процедурой ФОРМ (задача) формируется начальная популяция нач_попул. На каждой генерации (число генераций равно Т) сначала процедурой Генетика(нач_попул) реализуются генетические операторы, синтезирующие новые решения, в результате образуется расширенная популяция тек_попул. Процедурой АД_СЕЛЕКТ в популяции тек_попул отбирается множество решений нач_адапт для дальнейшей обработки адаптивным обучающимся алгоритмом. Отметим, что в множество нач_адапт не включаются решения, полученные алгоритмом адаптивного обучения и не подвергавшиеся дальнейшим изменениям генетическими операторами. Далее каждое решение множества нач_адапт с помощью процедуры АДАПТ(нач_адапт) подвергается обработке алгоритмом адаптивного обучения, и получается множество решений адапт. Полученные решения процедурой ОБЪЕДИНИТЬ(тек_попул,адапт) включаются в популяцию тек_попул. В заключении процедурой СЕЛЕКТ(тек_попул) на базе популяции тек_попул осуществляется отбор и формирование популяции нач_попул. Дополнительным источником усовершенствования является правильная настройка параметров управления. Для увеличения скорости генетического поиска осуществляется адаптация виртуального набора популяций. Суть заключается в смене виртуальной популяции, если в течение некоторого числа генераций в ней не появляются решения с лучшим значени- ем ЦФ. Для реализации механизма адаптации каждому вектору Bl сопоставляется АА al c двумя группами состояний. На рисунке 5 приведена граф-схема переходов АА. Две группы состояний S1 и S2 соответствуют двум альтернативам: A1=Г(S1) – вектор Bl остается без изменений; A2=Г(S2) – вектор Bl меняется. Входной алфавит Q={+,-,R} включает возможные отклики среды – поощрение (+) и наказание (-), а также сигнал возврата R. Выработка управляющих сигналов (+) или (-) осуществляется следующим образом. Обозначим через gl лучшее значение ЦФ для виртуальной популяции vl, то есть ("j)[ gl³Fjl], l=const. Пусть vl* – виртуальная популяция, для которой gl – худшее (наименьшее значение), которое обозначим как min. Если в популяции vl после выполнения очередной генерации произошло улучшение показателя gl, то вырабатывается сигнал поощрение (+), в противном случае вырабатывается сигнал наказание (-). Процесс адаптации на каждой генерации реализуется за четыре такта: 1) для всех выбранных популяций рассчитывается показатель gl; 2) вырабатываются отклики среды – сигналы (+) или (-); 3) под действием откликов осуществляются переходы в АА в соответствии с граф-схемой переходов. Отметим, что в состоянии S2 АА ai попадает, если в течение q генераций подряд не было улучшения gl; 4) реализуются альтернативы в соответствии с состояниями АА. Возможны три варианта реализации альтернатив. При первом варианте у всех виртуальных популяций vl, для которых соответствующие им АА находятся в состоянии S2, осуществляется смена векторов Bl. Смена Bl заключается в генерации случайным образом нового Bl. Во всех вариантах после смены вектора Bl на вход АА подается сигнал R (возврата), по которому осуществляется переход в группу S1. При втором варианте смена Bl осуществляется только в том случае, если gl имеет худшую оценку среди всех остальных. При третьем варианте смена вектора Bl осуществляется только в том случае, если оценка gl для vl имеет худшее значение среди оценок тех виртуальных популяций, для которых АА выдавали команду сменить.
При смене Bl анализируется расширенная популяция генотипов Rи. Если существует пара (Bl,Hj)ÎRи, то на основе Bl¢ строится Hj¢ такая, чтобы решения рi на базе (Bl, Hj) и на базе (Bl¢,Hj¢) были идентичны. После этого в популяции Пи осуществляется смена Hj на Hj¢. Следовательно, при смене B1 лучшие решения pi, входящие в популяцию решений Р, не изменяются. Использование рассмотренных средств и методов поисковой адаптации позволило синтезировать эффективные алгоритмы автоматизированного проектирования СБИС [6]. Список литературы 1. Holland J.H. Adaptation in Natural and Artificial Systems. An Introductory Analysis with Application to Biology, Control, and Artificial Intelligence. University of Michigan, 1975, 210 p. 2. Handbook of Genetic Algorithms, Edited by Lowrence Davis, Van Nostrand Reinhold, New York, 1991. 385p. 3. Курейчик В.М., Лебедев Б.К., Лях А.В. Проблемы эволюционной адаптации в САПР. // Новинтех. - 1991. - №3. 4. Курейчик В.М. Генетические алгоритмы: Монография. - Таганрог: Изд-во ТРТУ. - 1998. - 242 с. 5. Батищев Д.И. Генетические алгоритмы решения экстремальных задач: Учеб. пособие. - Воронеж: ВГТУ, 1995. 65 с. 6. Лебедев Б.К. Методы поисковой адаптации в задачах автоматизированного проектирования СБИС: Монография. - Таганрог: Изд-во ТРТУ, 2000. - 192 c. 7. Букатова И.Л. и др. Эвоинформатика. Теория и практика эволюционного моделирования. – М.: Наука, 1991. 8. Венда В.Ф. Системы гибридного интеллекта. Эволюция, психология, информатика. – М.: Машиностроение, 1990. - 448 с. 9. Поспелов Д.А. Фантазия или наука: на пути к искусственному интеллекту. – М.: Наука, 1982. – 224 с. 10.Растригин Л.А. Адаптивные компьютерные системы. – М.: Знание, 1987. – 64 с. 11.Лебедев Б.К. Адаптация в САПР: Монография. - Таганрог: Изд-во ТРТУ, 1999. - 160 с. 12.Цетлин М.Л. Исследования по теории автоматов и моделированию биологических систем. – М.: Наука, 1969. – 316 с. 13.Курейчик В.М., Лебедев Б.К. Искусственный интеллект в САПР: Текст лекций. - Таганрог: ТРТИ, 1989. - 48 с. |
| Permanent link: http://swsys.ru/index.php?id=715&lang=en&page=article |
Print version Full issue in PDF (1.30Mb) |
| The article was published in issue no. № 1, 2002 |
Perhaps, you might be interested in the following articles of similar topics:
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
- Информационная поддежка технического обеспечения кораблей при первой операции флота
- Системы компьютерной поддержки процессов анализа, синтеза и планирования решений в условиях неопределенности
- Опыт разработки и эксплуатации системы управления базами данных (DBS/R)
- Формулировка задачи планирования линейных и циклических участков кода
Back to the list of articles
 Автомат с линейной тактикой, граф которого показан на рисунке 2, имеет две цепочки состояний. В состояниях S11¸S1m выбирается первая альтернатива (А1), в состоянии S21¸S2m – вторая (А2).
Автомат с линейной тактикой, граф которого показан на рисунке 2, имеет две цепочки состояний. В состояниях S11¸S1m выбирается первая альтернатива (А1), в состоянии S21¸S2m – вторая (А2).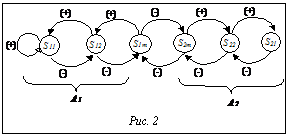 Параметр m характеризует глубину памяти АА, его способность к инерции сохранения альтернативы (действия) при удачах.
Параметр m характеризует глубину памяти АА, его способность к инерции сохранения альтернативы (действия) при удачах.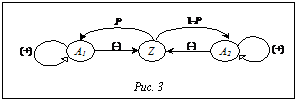 Особенностью адаптивных обучающихся алгоритмов является то, что они легко и достаточно быстро находят оптимальное решение, лежащее в некоторой достаточно обширной окрестности начальной точки поиска в пространстве решений. Как правило, за границы этой окрестности алгоритм не выходит, и если решение с глобальным оптимумом лежит вне этой окрестности, то оно не будет найдено. Для решения этой проблемы, с одной стороны, разрабатываются структуры поиска и механизмы вероятностных обучающихся автоматов, увеличивающих размеры окрестности, а с другой стороны, используется метод “набрасывания”, суть которого в выборе нескольких точек начального поиска, последовательной реализации алгоритма для каждой из них и в выборе лучшего решения.
Особенностью адаптивных обучающихся алгоритмов является то, что они легко и достаточно быстро находят оптимальное решение, лежащее в некоторой достаточно обширной окрестности начальной точки поиска в пространстве решений. Как правило, за границы этой окрестности алгоритм не выходит, и если решение с глобальным оптимумом лежит вне этой окрестности, то оно не будет найдено. Для решения этой проблемы, с одной стороны, разрабатываются структуры поиска и механизмы вероятностных обучающихся автоматов, увеличивающих размеры окрестности, а с другой стороны, используется метод “набрасывания”, суть которого в выборе нескольких точек начального поиска, последовательной реализации алгоритма для каждой из них и в выборе лучшего решения. В общем случае адаптивная поисковая процедура на основе самообучения и самоорганизации включается в структуру процедуры генетического поиска. На рисунке 4 приведен псевдокод комбинированной адаптивной поисковой процедуры.
В общем случае адаптивная поисковая процедура на основе самообучения и самоорганизации включается в структуру процедуры генетического поиска. На рисунке 4 приведен псевдокод комбинированной адаптивной поисковой процедуры.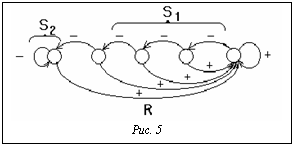 Пусть Bl – обозначение до смены, а Bl¢ – после смены. Смена Bl на Bl¢ осуществляется случайным образом. Между Bl и Bl¢ устанавливается соответствие Г(Bl,Cl,Bl¢).
Пусть Bl – обозначение до смены, а Bl¢ – после смены. Смена Bl на Bl¢ осуществляется случайным образом. Между Bl и Bl¢ устанавливается соответствие Г(Bl,Cl,Bl¢).