Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (malyukov@fep.tsure.ru) - , Russia, Ph.D, () - | |
| Ключевое слово: |
|
| Page views: 10035 |
Print version Full issue in PDF (1.30Mb) |
Существенное расширение применения стекловидных диэлектриков в качестве высокотемпературных покрытий обусловливает интерес к изучению и описанию зависимостей свойств уникального материала при изменении его состава и условий тепловой отработки. Например, проектирование магнитных головок для аппаратуры магнитной записи и головок, используемых в накопителях информации, является высокотехнологичным дорогостоящим этапом производства, связанным с длительным подбором состава, – формирование компонентов c необходимыми свойствами и их спаев, которые удовлетворяли бы требованиям прочности и износостойкости, размещению температурных полей и другим критериям, применяемым к конструкциям магнитных головок. Поэтому важным моментом является автоматизированный расчет температурных полей в спаях стекловидного диэлектрика с металлом. Наиболее значимым свойством для теории и практики высокотемпературных покрытий является их термостойкость, для изучения которой требуется расчет температурных полей и напряжений, возникающих в покрытии в различных условиях службы изделий [1]. Зная температурные напряжения, можно определить допустимые для данного покрытия границы применения. Покрытие имеет значительно меньшую толщину по сравнению с покрываемой деталью, поэтому найдем температурные поля в наиболее простом варианте – покрытие по плоскости, достаточно полно описывающее распределение температур. Рассмотрим задачу охлаждения (нагревания) полосы металла, покрытой с двух сторон стекловидным диэлектриком. Математическая постановка задачи (рис. 1):
Здесь q1 и q2 – избыточные температуры в покрытии и полосе; a1 и a2 – температуропроводность покрытия и полосы; t – время нагревания (охлаждения); z – координата; h и h1 – толщина покрытия и половина толщины полосы; Для решения применяем метод разделения переменных Фурье [2] при дополнительных предположениях: Разложив полученное решение в ряд по степеням h и ограничившись конечным числом слагаемых, количество которых определяется погрешностью начальных условий, получаем достаточно простые уравнения для нахождения собственных чисел задачи (1)-(7). Сделаем в уравнении (1) и граничном условии (3) замену переменных Тогда уравнения (1) и (3) запишутся следующим образом:
Методом Фурье [3] определяем частное решение уравнения (10) в виде: Для удовлетворения граничным условиям, подставляя (12) в (11), приходим к следующему равенству:
Решение задачи (2):
Из (5):
Подставляем (14) в граничное условие (4), затем (14) и (12) в граничное условие (6). Окончательно получаем следующую систему уравнений:
В (16) учтено, что Анализируя систему (16), замечаем, что Аналогично: Подставляем в (16) разложения по степеням
Первое уравнение системы (17) является трансцендентным и имеет бесчисленное множество корней Для того чтобы удовлетворить начальным условиям (7), ищем решение задачи (1)–(7) в виде:
Возвращаясь к переменной z (9) и учитывая, что
окончательно получим:
Учтем равенство (18), тогда:
Подставляем последнее соотношение в выражение для
Учитываем начальное условие (7):
получим: где: Un(z)=
Во второй формуле равенства (22) сделаем замену:
Введем единую переменную x:
Легко можно проверить, что функции
Сделаем в выражении (21) замену (23), получим:
где Умножим ряд (26) на
Из последнего равенства находим коэффициент По формулам (19), (20) можно установить температурные поля в покрытии (стекле) и металле (полосе) при различных условиях теплообмена на границе покрытия (окружающая среда).
Покрытия наносили на полосы технического титана ВТ–1 и стали СТ–3 методом центрифугирования суспензий стекловидного диэлектрика. Испытания проводили сбрасыванием образцов, нагретых до определенной температуры, в резервуар с холодной водой. При проведении пробных расчетов по формулам (19) и (20) определили, что изменение температуры в покрытии со временем определяется в основном величиной критерия, который характеризует скорость теплообмена на границе и скорость притока тепла к границе из объема покрытия:
где h – толщина покрытия; l1 – теплопроводность покрытия; Таким образом, используя полученные формулы (19), (20), возможно построение автоматизированной системы расчета температурных полей в спаях стекловидного диэлектрика с металлом. Назначение разрабатываемого алгоритма – определить толщину покрытия и материал, из которого оно изготовлено. При этом металл, на который наносится покрытие, выбирается изначально. Целевой функцией в данном алгоритме является коэффициент Ci, который задается пользователем в начале работы программы. Он зависит от толщины покрытия и от теплофизических данных материалов (таблица 2): l1 – теплопроводность покрытия; æ – коэффициент теплоотдачи на границе покрытия (внешняя среда). Коэффициент Ci также зависит от констант, которые определяются составом материала (таблица 3).
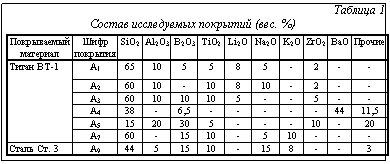
В начале работы алгоритма, используя экспериментальные составы покрытий, приведенных в таблице 1, определяется интервал для каждого из параметров, то есть определяется область поиска. Для каждого из параметров задается целевое значение, к которому параметр должен стремиться, а также приоритет параметра, чтобы пользователь мог регулировать важность параметра. Далее осуществляется полный перебор с заданным шагом точности с использованием формул (19), (20). После того как найдены значения всех параметров, получаем состав покрытия и его толщину, используя математическую модель, описывающую зависимость состава материала от его теплофизических параметров. Данная математическая модель создается с использованием метода Брандона [6].
Для реальных покрытий (при небольших толщинах) значение критерия Ci колеблется в пределах от 0,1 до 100. При Ci < 0,1 температуру по всему сечению покрытия можно принять постоянной, то есть градиентом температуры можно пренебречь, а при Ci > 100 температура поверхности и окружающей среды выравнивается, и формулы (19) и (20) значительно упрощаются. Список литературы 1. Журавлев Г.И. Химия и технология термостойких неорганических покрытий. - М.: Химия. – 1975. - 198 с. 2. Смирнов В.И. Курс высшей математики. - М.: Наука. - 1979. - Т.4. - 652 с. 3. Олвер Ф. Введение в асимптотические методы и специальные функции. - М.: Наука - 1978. - 375 с. 4. Малюков С.П. Стекловидные диэлектрики в производстве магнитных головок. (Монография). - Изд–во ТРТУ, 1998. 5. Капустин Н.М., Васильев Г.Н. Автоматизация конструкторского и технологического проектирования. - М.: Высшая школа, 1986. - Кн. 6. 6. Малюков С.П., Обжелянский С.А. Алгоритм формирования математической модели синтеза стекловидных диэлектриков для магнитных головок. // Изв. ТРТУ.- Таганрог. - №4. - 2001. |
| Permanent link: http://swsys.ru/index.php?id=721&lang=en&page=article |
Print version Full issue in PDF (1.30Mb) |
| The article was published in issue no. № 1, 2002 |
Perhaps, you might be interested in the following articles of similar topics:
- Эвристические и точные методы программной конвейеризации циклов
- Разработка загрузчика программного обеспечения встроенной системы управления
- Компьютерные технологии сегодня: тенденции и прогнозы
- Система моделирования и оценки эффективности торговых стратегий
- Алгоритмы и процедуры построения билинейных моделей непрерывных производств
Back to the list of articles
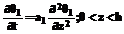 , (1)
, (1)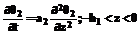 , (2)
, (2)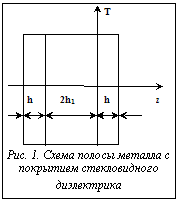
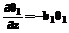 , z=h, (3)
, z=h, (3)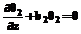 , z=-h1, (4)
, z=-h1, (4)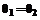 , z=0, (5)
, z=0, (5)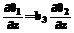 , z=0, (6)
, z=0, (6)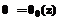 , t=0. (7)
, t=0. (7)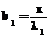 ,
,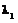 – теплопроводность покрытия, x – коэффициент теплоотдачи на границе раздела покрытие–внешняя среда; b2 – теплопроводность полосы; b3 – отношение теплопроводности полосы и покрытия; q0(z) – начальная избыточная температура полосы и покрытия по отношению к внешней среде.
– теплопроводность покрытия, x – коэффициент теплоотдачи на границе раздела покрытие–внешняя среда; b2 – теплопроводность полосы; b3 – отношение теплопроводности полосы и покрытия; q0(z) – начальная избыточная температура полосы и покрытия по отношению к внешней среде.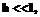
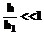 . (8)
. (8)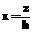 . (9)
. (9)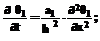 0 < x < 1; (10)
0 < x < 1; (10)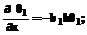 (x = 1). (11)
(x = 1). (11)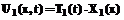 , тогда
, тогда 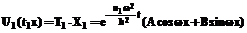 . (12)
. (12)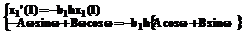 . (13)
. (13)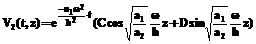 . (14)
. (14)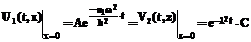 . (15)
. (15)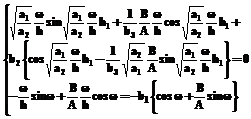 (16)
(16)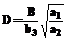 .
.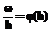 , то есть
, то есть 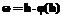 и
и 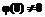 , то есть
, то есть 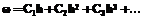 .
.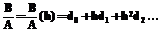 , где через
, где через 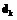 обозначим коэффициенты разложения при
обозначим коэффициенты разложения при  выражения
выражения 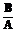 по степеням
по степеням 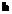 .
. функции
функции 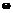 и
и 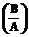 и положим в полученных равенствах
и положим в полученных равенствах  . В результате приходим к системе уравнений для нахождения нулевых членов асимптотики по
. В результате приходим к системе уравнений для нахождения нулевых членов асимптотики по  и
и  и
и 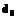 .
.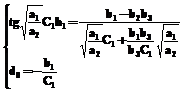 (17)
(17) .
.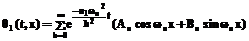 .
.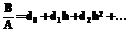 , то есть, что
, то есть, что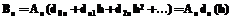 , (18)
, (18)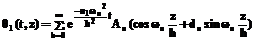 , (19)
, (19)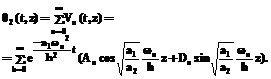
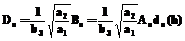 .
.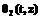 :
: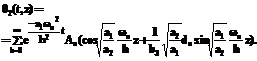 (20)
(20)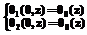
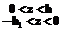 ,
,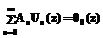 , (21)
, (21)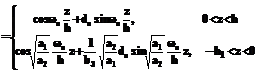 (22)
(22)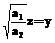 . (23)
. (23)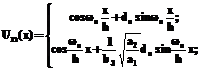
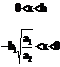 (24)
(24)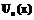 ортогональны, то есть:
ортогональны, то есть: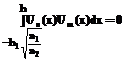 , где
, где 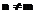 . (25)
. (25)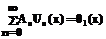 , (26)
, (26)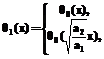
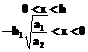
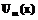 и проинтегрируем в пределах
и проинтегрируем в пределах 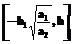 . Тогда, учитывая (25), получим:
. Тогда, учитывая (25), получим: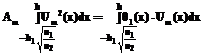 . (27)
. (27)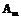 , тем самым удовлетворено начальное условие (7) и задача (1)–(7) полностью решена.
, тем самым удовлетворено начальное условие (7) и задача (1)–(7) полностью решена.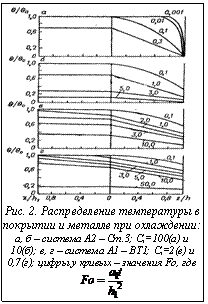 Расчеты приведены для покрытий, составы которых представлены в таблице 1. Составы стекловидных диэлектриков и теплофизические параметры взяты из работы [4].
Расчеты приведены для покрытий, составы которых представлены в таблице 1. Составы стекловидных диэлектриков и теплофизические параметры взяты из работы [4].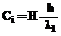 , (28)
, (28)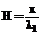 .
. Для поиска состава материала и толщины покрытия, которые описывает целевая функция в виде коэффициента Ci, применяем алгоритм эвристического перебора [5].
Для поиска состава материала и толщины покрытия, которые описывает целевая функция в виде коэффициента Ci, применяем алгоритм эвристического перебора [5].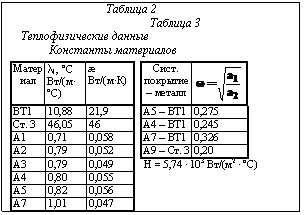 В завершении работы автоматизированной системы строятся графики распределения температуры в покрытии и металле при охлаждении и изменения температуры на поверхности покрытия и на границе покрытия с металлом от времени охлаждения. Результирующие графики работы программы приведены на рисунке 2.
В завершении работы автоматизированной системы строятся графики распределения температуры в покрытии и металле при охлаждении и изменения температуры на поверхности покрытия и на границе покрытия с металлом от времени охлаждения. Результирующие графики работы программы приведены на рисунке 2.