Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Keywords: , methods, domain ontology, database |
|
| Page views: 14141 |
Print version Full issue in PDF (1.83Mb) |
Онтология описывает понятия предметной области, включает машиночитаемые определения основных понятий и отношений между ними. В этом смысле знания становятся возможными для повторного использования людьми, базами данных и приложениями. При этом значительно повышается эффективность как интеллектуальных, так и традиционных информационных систем. Это определяет актуальность создания онтологий.
К настоящему времени разработано достаточно много систем, позволяющих в диалоговом режиме создавать онтологии. Однако этот процесс характеризуется высокой трудоемкостью. Поэтому знания о понятиях необходимо извлекать из полнотекстовых источников знаний автоматически. Ядром онтологии предметной области является терминосистема, для создания которой знания необходимо извлекать из терминологических словарей. Для автоматического построения номенклатуры [1], являющейся проекцией терминосистемы на подобласти знаний, знания можно извлекать из научных и учебных изданий. Построение онтологии предметной области выполняется на основе единого категориального аппарата, при этом вначале создается терминосистема, а затем номенклатуры. Соединение номенклатуры и терминосистемы Присоединение вновь создаваемой номенклатуры NS к существующей терминосистеме ТS той же предметной области выполняется в процессе представления нового термина. По каждому новому термину tkNSÎTermNS (где TermNS – множество терминов номенклатуры NS) должен выполняться поиск по образцу данного термина в терминосистеме ТS. Пусть имеем два образца tiТS и tkNS, соответствующие имени термина в терминосистеме ТS и номенклатуре NS:
где z1 – имя термина; z2 – тип термина; z3 – вид сущности; хij – значение tiTS для терминосистемы; ykj – значения для номенклатуры. Если соответствующие хij и ykj равны, то термину tkNS соответствует термин tiTSÎTermTS, где TermTS – множество терминов терминосистемы ТS. Однако возможны случаи, когда в образце tkNS неизвестны значения yk2 и/или yk3, так как в научном тексте информация о термине может быть неполной. Тогда, если хi1=yk1, будем считать, что термину tkNS соответствует термин tiTSÎTermTS. Если термин найден, то в соответствующую вершину семантической сети G или слота знака-фрейма F необходимо записать ссылку на термин tiTS терминосистемы. Кроме того, необходимо добавить записи в заголовки терминосистемы и номенклатуры. В общем виде заголовок терминосистемы и номенклатуры имеет одинаковую структуру: <Имя предметной области = <…> <Присоединенная предметная область <Уровень предметной области = верхний|нижний> <Тип предметной области = терминосистема| |область знаний|задача|вид деятельности> <Имя присоединенной подобласти знаний = <имя> <Имя связывающего термина = <…> > … > Вполне возможно, что некоторые термины номенклатуры имеют имя, не совпадающее с именем термина в терминосистеме, но по сути являются квазисинонимами. Поэтому после создания номенклатуры необходимо выполнить сравнение интенсионалов терминов номенклатуры и терминосистемы. Интенсионал термина типа «Понятие» определяется кортежем: T=, где t – имя термина, заданное вектором Z=; D – множество дефиниций термина; Pr – множество свойств термина; A – множество действий; C – кортеж, состоящий из множества синонимов и множества коррелятов термина; K – множество терминов, находящихся в квалитативных отношениях с термином t; М – множество метазнаков. Так как элементами вектора Т являются в основном множества, анализ будем проводить по "tiÎТ, причем существенными будем считать множества Pr, K. Нельзя сказать, что множества C, М и A несущественны. Но, как правило, в научном тексте рассматриваются отдельные стороны термина, касающиеся какой-либо проблемы или задачи, поэтому для номенклатуры они несущественны. Для анализа интенсионалов будем использовать отношение сравнения элементов вектора Т, которое рассмотрим по каждой паре терминов (ti,tj), такой, что tiTSÎTermTS, tjNSÎTermNS. Обозначим символом Х множества вектора TermTS, а Y – множества вектора TermNS, то есть при рассмотрении элемента «Свойства» вектора Т Х=PriTS, а Y=PrjNS, где множество PriTS задает свойства tiTÎTermTS, а множество PrjNS – свойства tiNSÎTermNS. При анализе TiTS и TjNS отношение сравнения должно применяться для множеств терминов, связанных родовидовым отношением и отношением часть-целое. Таким образом, в сравнении участвуют множества свойств, родовых и видовых терминов, терминов типов целое и часть. Отношение сравнения множеств. Для сравнения множеств X и Y будем использовать отношения: Y¹Х, Y=Х, YÌХ, YÉХ, YÇХ¹Æ. Y¹Х. Если для любых X и Y отношение неравенства существует, то из этого следует, что термины tiTS и tjNS разные, и номенклатура остается в той же конфигурации. Y=Х. Если для любых X и Y отношение равенства существует, то термины идентичны. В этом случае в знаке-фрейме FNT, соответствующем данному термину в номенклатуре NT, необходимо удалить всю информацию, кроме заголовочной, в которую нужно добавить ссылку на FST. Тогда в знаке-фрейме FNT остается только имя термина tjNS и ссылка на tiTS. В том случае, если имена терминов не совпали, а для остальных множеств существует отношение равенства, то из этого следует, что термин tjNS является синонимом tiTS, и во множество синонимов нужно включить имя термина и ссылку на него. YÌХ. Если для любых X и Y отношение включения YÌХ истинно, то рассматриваемый термин tjNS наследует свойства термина tiTS. Тогда в FNT термина tjNS необходимо удалить всю информацию, кроме заголовочной, в которую добавляется ссылка на FST. YÉХ. Если для любых X и Y отношение включения YÉХ истинно, то это означает, что рассматриваемый термин tjNS обладает более полным описанием, чем термин tiTS, и его знак-фрейм FST необходимо дополнить недостающей информацией из знака-фрейма FNT, затем удалить всю информацию из знака-фрейма FNT, кроме заголовочной, в которую добавляется ссылка на FST. Надо отметить, что вероятность существования отношений равенства и включения на множествах X и Y невелика. Наиболее частым является случай, когда истинно отношение YÇХ¹Æ. Для его анализа лучше всего использовать аппарат нечеткой логики, позволяющий рассматривать различные ситуации, например такие: – часть свойств совпала в основном, и мощность множества пересечения родовых понятий большая, мощность множества пересечения видовых понятий небольшая, а мощности множеств пересечения других множеств ничтожно малы, то можно сказать, что термин tiTS в научном тексте рассматривается под другим углом (этой ситуации, скорее всего, соответствует вывод о том, что в номенклатуре определен новый вид tjNS как отображение термина tiTS); – часть свойств совпала в основном, и мощность множества пересечения родовых понятий небольшая, мощность множества пересечения видовых понятий большая, а мощности множеств пересечения других множеств ничтожно малы, то можно сказать, что термин tiTS в научном тексте является родом понятия tiTS. Таким образом, проекция терминосистемы TS на плоскость рассматриваемого научного текста в виде номенклатуры NS позволяет уточнять термины терминосистемы, определять новые виды терминов, новые компоненты терминов, то есть уточнять терминологию предметной области. Анализ отношения YÇХ¹Æ Для примера рассмотрим анализ отношения YÇХ¹Æ, которое может быть истинно для "(Yl, Хl), где l=1..5 и последовательно нумерует множества: свойств; родовых терминов; видовых терминов; терминов, означающих целое, и терминов, означающих часть. На практике могут встречаться различные комбинации истинности отношения YlÇХl¹Æ. Рассмотрим случай, когда отношение YlÇХl¹Æ истинно при l=1,2. Для анализа отношения YÇХ¹Æ используем метод нечеткого регулирования Мамдани [2]. Компоненты нечеткого вывода рассмотрим на примере определения степени достоверности того, что термин tjNS является новым видом термина ti-1TS. База правил нечетких продукций состоит из следующих элементов. Имя продукции: номер нечеткой продукции. Сфера применения: выявление нового вида термина. Условие применимости: " (Yl, Хl) YlÇХl¹Æ истинно, где l=1,2. Условие ядра: составное нечеткое высказывание вида «IS1=Dt¢ И IS2=Dt¢», где IS1, IS2 – обозначения входных лингвистических переменных InterSection, являющихся мощностью множеств YlÇХl; терм t¢ÎТ1={Маленький, Средний, Большой}; модификатор DÎM1={ОЧЕНЬ, НЕ, НИЖЕ, ВЫШЕ}. Заключение ядра: нечеткое высказывание вида «Out=Dt²», где Out – обозначение выходной лингвистической переменной: СТЕПЕНЬ ДОСТОВЕРНОСТИ ГИПОТЕЗЫ О НОВОМ ВИДЕ ТЕРМИНА, терм t²ÎТ2 и Т2={Низкая, Средняя, Высокая}; модификатор DÎM2 и M2={ДОСТАТОЧНО, НИЖЕ, ВЫШЕ}. Метод определения количественного значения степени истинности заключения ядра – метод min-активизации: Коэффициент определенности нечеткой продукции: F=1.
Чтобы определить вид зависимостей функции принадлежности нечетких множеств, рассмотрены основные типы и виды существующих функций принадлежности, которые могут быть использованы в решении поставленной задачи. Их анализ показал, что поставленным условиям наилучшим образом удовлетворяет колоколообразная функция. Этапы нечеткого логического вывода. Фаззификация нечетких переменных для входных лингвистических переменных рассматриваемого примера дает значения функций принадлежности, приведенные в таблице. Таблица Результат фаззификации входных лингвистических переменных
Процедура агрегирования нечеткого логического вывода сводится к выбору минимального значения функций истинности:
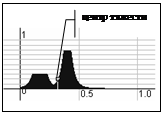
Результат агрегирования представляет собой множество степеней истинности условий правил нечетких продукций B={b1,…,bn}, где n – мощность множества правил нечетких продукций. Для рассматриваемого примера n=84. На этапе активизации степень истинности для терма выходной лингвистической переменной определяется по формуле: На этапе аккумуляции находим функцию принадлежности выходной лингвистической переменной методом max-объединения нечетких множеств C1,…,Cn: На рисунке приведен график функции принадлежности выходной лингвистической переменной. В качестве метода дефаззификации использован метод центра тяжести. На рисунке отмечен центр тяжести для рассматриваемой задачи, который показывает, что степень достоверности гипотезы о новом виде термина d=0,322. Это значение говорит о том, что мера возможности принятия данной гипотезы слишком мала. Описание системы нечеткого логического вывода Для проведения экспериментов и проверки корректности выдвинутых положений было разработано программное обеспечение. Архитектура нечеткого регулятора состоит из трех компонентов: базы правил, интерфейсной части, аппарата нечеткого вывода. Интерфейсная часть обеспечивает выполнение следующих функций: ввод исходных данных; создание, загрузка и сохранение базы правил нечетких продукций; ввод и редактирование переменных, термов, сфер и условий применимости, правил нечетких продукций на ограниченном подмножестве естественного языка; преобразование правила нечеткой продукции с естественно-языкового представления в предикатное; настройку методов логического вывода (активизации, аккумуляции и дефаззификации); отображение ре- зультатов нечеткого логического вывода в виде числовых данных и графиков функций принадлежности. В базе правил хранятся множества входных и выходных лингвистических переменных с соответствующими им терм-множествами; множество четких переменных; множество продукционных правил, включающих условие применимости правила, посылку и заключение. Аппарат нечеткого вывода выполняет нечеткий логический вывод с выбранной точностью и обосновано выбранными методами активизации, аккумуляции и дефаззификации. Предложенный подход соединения онтологий позволяет объединять онтологии одной предметной области на основе анализа интенсионалов терминов, принадлежащих терминосистеме и номенклатуре. Для этого выполняется сравнение отношений между соответствующими множествами интенсионалов, основанное на анализе отношений неравенства, равенства, включения и пересечения множеств, представляющих элементы интенсионала сравниваемых терминов, с применением нечеткого логического вывода. В работе показан способ введения нечеткости и пример применения методов нечеткого регулирования. Список литературы 1. Мельников Г.П. Основы терминоведения. - М.: Изд-во ун-та дружбы народов, 1991. – 116 с. 2. Асаи К., Ватага Д., Иваи С. и др. Прикладные нечеткие системы. / Под ред. Тэрано Т. – М.: Мир. – 1993. – 344 с. | ||||||||||||||||||||||||||||||||||||||
| Permanent link: http://swsys.ru/index.php?id=739&lang=en&page=article |
Print version Full issue in PDF (1.83Mb) |
| The article was published in issue no. № 2, 2008 |
Perhaps, you might be interested in the following articles of similar topics:
- Эффективная программная реализация вейвлет-преобразования
- Технология быстрой разработки баз данных и приложений пользователя в системе «COBRA++»
- Интеграция подпространства предметной области в семантическое пространство «математика»
- Требования к программной реализации системы Индустрии 4.0 для создания сетевых предприятий
- Алгоритмическое и программное обеспечение когнитивного агента на основе методологии Д. Пойа
Back to the list of articles
 Постусловия продукции: процедура модификации сети фрейм-знаков.
Постусловия продукции: процедура модификации сети фрейм-знаков.