Software & Systems

Логическое дифференциальное и интегральное исчисления являются направлениями современной дискретной математики и находят свое применение в задачах динамического анализа и синтеза дискретных цифровых структур. Основным понятием логического дифференциального исчисления является производная булевой функции, представление о которой в виде булевой разности было получено еще в работах [1,2]. Булева производная по некоторым своим свойствам является аналогом производной в классическом дифференциальном исчислении. Заметим, что идеи об определении булевой производной вряд ли могли бы появиться без известной алгебраической нормальной формы и представления логической функции в виде полинома Жегалкина [3]. Развитие дифференциального исчисления в области дискретной математической логики происходило в нескольких направлениях [4], и к настоящему времени в этой области достигнуто немало результатов. Тем не менее, на наш взгляд, недостаточно исследованными остаются две важных нерешенных задачи: задача о символьных (нечисленных) аналитических преобразованиях логических функций в стиле компьютерных алгебр в области логического дифференциального исчисления и задача доопределения понятия о булевых интегралах и выполнения аналитических логических интегральных преобразований, пригодных для реализации в алгоритмах компьютерных алгебр.

В данной работе обозначено решение поставленных задач, для чего авторами разработано алгоритмическое обеспечение и выполнена программная реализация алгоритмов.

Программные системы символьных вычислений открыли новые широкие возможности для поддержки теоретических и прикладных научных исследований. На протяжении почти четырех последних десятилетий компьютерные алгебры, начиная с системы MASCYMA, совершенствуются, приобретают улучшенные функциональные возможности. В их числе такие известные реализации, как MAXIMA, AXIOM, GAP, DERIVE, SINGULAR, NUMPI, OCTAVE, PARI/GP, YASIMCA, YACAS, и алгебраические возможности пакетов MAPLE, MATHCAD, MATLAB, R и прочих менее распространенных программных продуктов. Несмотря на такое разнообразие систем и предлагаемых ими символьных преобразований, ни одна из них не располагает функциональными возможностями аналитических преобразований в области логического дифференциального и интегрального исчислений. Причина тому – имеющаяся разрозненность в применяемой терминологии, способах исследований в данной области, что, естественно, не снижает актуальности этой тематики, а лишь подчеркивает настоятельные требования разработки единой методологической основы такой технологии динамического анализа и синтеза цифровых структур.

Обратимся к задаче символьного дифференцирования логических функций. Представляемый метод основан на нахождении частных булевых производных для полностью определенной логической функции. Алгоритм построен для производных ; его модификация для нахождения  весьма незначительная. В алгоритме используется код Грея, но его построение не вызывает особых трудностей и подробно не обсуждается.

Алгоритм 1. Символьное вычисление частных производных булевой функции.

На входе алгоритма имеется булева функция  от двоичных переменных.

1.    Формируется код Грея для  переменных  и в столбец  записываются значения исходной булевой функции f при соответствующих наборах аргументов.

2.    Выбирается переменная , , относительно которой будет выполняться операция символьного дифференцирования.

3.    Формируется пустая матрица , в которую затем записываются элементы в соответствии со следующими правилами.

4.    В цикле повторений в последнем столбце матрицы C следует найти наборы из двух соседних элементов, то есть тех, у которых вес Хэмминга равен 1.

4.1.     Если в сгруппированном наборе имеется одна 1 и один 0, также  и значение булевой функции , то такой набор считается сменой полярности булевой производной функции f (в связи с ее известным свойством).

4.2.     В ячейки матрицы D, которые соответ- ствуют индексам элементов найденного набора матрицы C, записывается некоторый заранее определяемый ключевой символ, например, знак «».

4.3.     Повторяются шаги 4.1 и 4.2.

5.    Выполняется символьная запись булевой производной путем сопоставления значения параметров булевой функции, записанной в матрицу G, и оставшихся наборов по следующему правилу. В каждом наборе для любого помеченного знаком «» элемента матрицы C выбираются переменные исходной булевой функции f, имеющие значение 1, которые затем включаются термами в выражение булевой функции, причем значение  в терм не вносится.

Пример. Пусть  .

Формирование матриц алгоритма для ¶F/¶x1 показано в таблице.

Таблица

Результат символьного вычисления частной булевой производной по переменной xi по примеру:

 = .

Целесообразно рассмотреть одну из возможных конструкций неопределенного интеграла, отмечая особо, что многовариантная природа логических функций обусловливает необходимость осторожного подхода к вопросу формирования конструкции интеграла булевой функции в части равенства или эквивалентности реализующих его формул. При исследовании учитывались результаты практически единственной существующей в этой области работы [5], в которой интеграл булевой функции f от n переменных введен следующим образом:

.                                (1)

Доопределим это понятие. Очевидно, что (1) не является логической переключательной функцией. Обозначим «» и «» операторы логического переключения булевой функции из состояния 0 в состояние 1 и из состояния 1 в состояние 0 соответственно. Тогда полная конструкция неопределенного булева интеграла будет записываться в виде:

Часть таблицы истинности логической функции содержит результат 1, а остальная часть дает в результате 0, поэтому целесообразно ввести неопределенные интегралы «результирующие 1» и «результирующие 0» в виде

,                        (2)

.                        (3)

Полный неопределенный булев интеграл существует тогда, когда найдутся независимые друг от друга дискретные функции  и , имеющие не менее n реализаций, чтобы , в таком случае можно утверждать, что , если . Необходимым условием существования неопределенного булева интеграла можно считать .

Теперь на основе алгоритма 1 нахождения частных производных и выражений (2) и (3) можно предложить алгоритм символьного вычисления булева интеграла.

Алгоритм 2. Символьное вычисление булева интеграла.

1.    Выполнить шаги алгоритма 1 для нахождения всех n частных производных заданной булевой функции с сохранением результатов.

2.    Сформировать матрицу , заполнив столбцы  по принципу кода Грея.

3.    Заполнить столбец  матрицы I символом 1, если вычисление по (2) дает в результате 1.

4.    Заполнить столбец  матрицы I сим- волом 0, если вычисление по (3) дает в результа- те 1.

5.    Заполнить единицами все ячейки столбца  матрицы I, если расстояние Хэмминга соседней с ними ячейке равно 1.

6.    Выполнить символьную запись термов булева интеграла, аналогично п. 5 алгоритма 1, причем между термами использовать знак «+».

7.    После группировки всех слагаемых, входящих в частную производную по переменной, выражение заключить в скобки и применить обозначение дифференциала по переменной.

Для функции из ранее приводимого примера выполнение шагов алгоритма 2 приводит к следующей символьной записи:

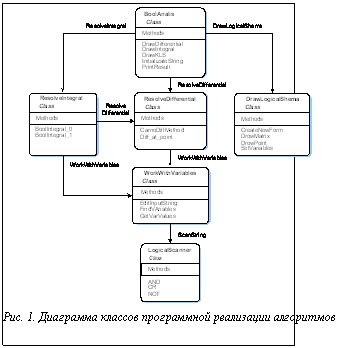
Алгоритмы 1 и 2 были реализованы в системе программирования Visual Studio.Net с применением языка программирования C#. Программный комплекс имеет структуру классов, показанную на рисунке 1, которая отображена в виде иерархической диаграммы классов использования, то есть класс, вызывающий методы других, находится выше по диаграмме, а предоставляющий методы – ниже.

Класс WorkWithVariables предназначен для формирования массивов переменных, определения их числа, и в зависимости от результатов он позволяет обновлять таблицы истинности класса BoolAnalis и форму ввода данных. Методы класса DrawLogicalSxema, предназначенные для работы с интерфейсом пользователя, позволяют отобразить полученный результат в символьном виде и в виде модели контактной логической схемы. Методы класса ResolveDifferential предоставляют функции определения выражения производной по n переменным и позволяют получить значение производной при заданных значениях переменных. Класс ResolveIntegral, который использует методы класса ResolveDifferential, позволяет определить и минимизировать значения Integral_0 и Integral_1. Класс BoolAnalis содержит функции, основной задачей которых является вызов методов других классов для получения таблиц истинности и выражений исходной функции, булевой производной и интеграла, а также вызов методов работы с интерфейсом.

Интерфейс программы и результаты исполнения показаны на рисунках 2 и 3.

В разработанной программе для синтаксического распознавания строковых выражений использовался вычислительно эффективный метод рекурсивного спуска, модифицированный следующим образом. Основной идеей модификации является «зашивание» правил грамматики непосредственно в управляющие конструкции распознавателя. Идеи нисходящего разбора, принятые в LL(1)-грамматиках, в нем полностью сохраняются: происходит последовательный просмотр входной строки слева направо; очередной символ входной строки является основанием для выбора одной из правых частей правил группы при замене текущего нетерминального символа; терминальные символы входной строки и правой части правила взаимно уничтожаются; обнаружение нетерминального символа в правой части рекурсивно повторяет этот же процесс. В методе рекурсивного спуска идеи претерпевают такие изменения: каждому нетерминальному символу соответствует отдельная вычислительная подпрограмма, распознающая, выбирающая и закрывающая одну из правых частей правила, имеющего в левой части этот нетерминальный символ (то есть для каждой группы правил пишется свой распознаватель); во входной строке имеется указатель (индекс) на текущий закрываемый символ. Этот символ и является основанием для выбора необходимой правой части правила. Сам выбор встроен в распознаватель в виде алгоритмических конструкций языков программирования if и switch. Правила выбора базируются на построении множеств выбирающих символов, как это принято в LL(1)-грамматике; просмотр выбранной части реализован в тексте процедуры-распознавателя путем сравнения ожидаемого символа правой части и текущего символа входной строки; если в правой части ожидается терминальный символ и он совпадает с очередным символом входной строки, то символ во входной строке пропускается, а распознаватель переходит к следующему символу правой части; несовпадение терминального символа правой части и очередного символа входной строки свидетельствует о синтаксической ошибке; если в правой части встречается нетерминальный символ, то для него необходимо вызвать аналогичную распознающую подпрограмму.

Список литературы

1      Reddy, S.M. Easily Testable Realizations for Logic Functions // IEEE Trans. Computers. Vol. 21, no. 11, Nov., 1972.

2      Muller, D.E. Application of Boolean algebra to switching circuits design and to error detection // IRE Trans. Electron. Comp. Vol. EC-3, 1954., р. 6-12.

3      Жегалкин И.И. О технике вычислений предложений в символической логике. // Матем. сб. - 1927. - № 34. - С. 9-28.

4      Янушкевич С., Бохманн Д., Станкович Р., Тошич Ж., Шмерко В. Логическое дифференциальное исчисление: достижения, тенденции и приложения. // Автоматика и телемеханика. - 2000. - № 6. - С. 155-170.

5      Tucker, J.H. Tapia, M.A. Bennett, A.W. Boolean Integral Calculus for Digital Systems // IEEE Trans. On Comp., vol. 34, issue 1, Jan. 1985, p. 78-81.