Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - , () - | |
| Ключевое слово: |
|
| Page views: 12437 |
Print version Full issue in PDF (1.18Mb) |
Разработка программных продуктов требует математического моделирования объектов программирования. Обзор многочисленной научно-технической информации по проблемам математического, в том числе концептуального моделирования позволяет утверждать, что общих подходов в этом разделе теории сложных технических систем пока не существует, а проблемы концептуального моделирования систем решаются выборочно [1-3] или не решаются вообще. Однако многие авторы научных трудов в области моделирования единодушны в том, что концептуальные модели как смысловые структуры понятий и их отношений для некоторых предметных областей знаний весьма полезны. Они позволяют формализовать процедуры создания математических моделей, с помощью которых затем разрабатываются пакеты программ, реализующие, например, информационные технологии контроля и диагностики состояния объектов.
Концептуальные модели, в отличие от концепций, всегда представляются на дескриптивном (формализованном) уровне описания. Дескриптивное представление концептуальных моделей выполняется в форме символьной записи, например, в терминах теории высказываний, теории отношений или теории множеств, а также в форме структуры функциональных подсистем, блок-схем, таблиц, диаграмм, временных диа- грамм и т.д. Концептуальные модели позволяют выделить наиболее значимые функции концептуально представленной системы, уточнить свойства взаимодействия и взаимосвязи ее элементов, выделить наиболее существенные из них и определить множества искомых параметров и аргументов. Концептуальные модели позволяют, если это требуется, провести аппроксимацию задач ис- следования систем общеизвестными методами. В этой связи можно утверждать, что концептуальная модель есть формализованная концепция. Построение концептуальной модели как второй этап исследования сложной технической системы начинается с рассмотрения ее под каким-либо углом зрения, выбранным в соответствии с главной целью исследования. При этом в соответствии с выбранными методами моделирования может быть создано большое число концептуальных моделей одной и той же системы. Как показывает опыт авторов данной статьи, очень удобным и весьма продуктивным методом построения концептуальных и математических моделей, а затем и программных комплексов для автоматизированных систем контроля и диагностики состояния сложных энергетических объектов, таких как турбогенераторы, асинхронные агрегаты, трансформаторы и т.п., является использование для этих целей теории шкал. В основе теории шкал лежит теоретико-множественный аппарат отношений. В теории шкал исследуются различные свойства разнообразных объектов. Простейшим отношением между двумя свойствами является субъективное суждение о том, что одно из них больше (меньше) другого. Если ввести еще и третью оценку, лежащую между двумя первыми, то оценку каждого из первых двух можно определять отношением к третьему. Эти отношения поддаются математическому описанию на языке теории отношений. Пусть S – множество значений весов a, b, c объектов A, B, C, а R – отношение между объектами по их весам. Тогда суждение о том, что объект A весом a, "больше, чем" объект B весом b может быть записано как отношение aRb. Систему E = {S,Rj} (1) называют эмпирической системой с отношениями, если S – множество свойств объектов, а Rj – множество отношений между объектами по этим свойствам. Для того чтобы придать высказываниям об эмпирической системе численные (количественные) значения, ее отображают на числовую систему или наделяют метрикой, или нормой. Тогда одномерную числовую систему
называют абстрактной системой с отношением, если M – множество чисел (например всех действительных чисел), а Pj – отношения на числах, которые зависят от выбора числовой системы так, чтобы с их помощью легко и однозначно отражались бы соответствующие отношения из эмпирической системы. Равноценное отображение системы E на системе N называют гомоморфизмом, а совокупность правил, которые позволяют выполнить сопоставление (установить гомоморфизм) эмпирической системы с отношением в числовую систему с отношением, называют шкалой [4]. Любая шкала Шi может быть представлена тройкой: Шi = {E, N, ψ}, (3) где ψ – конкретный аналитический или алгоритмический способ гомоморфного отображения E на N. Другими словами, измерительная шкала задается на некотором множестве свойств E и ставит в соответствие свойству объекта некоторое число из множества чисел N, которое определяется по правилу построения шкалы, то есть по правилу ψ. Выделяя отдельные свойства или группу свойств моделируемой системы, можно создать множество шкал. При этом каждая шкала будет отражать выделенные свойства в одномерное метрическое, или нормированное пространство. Применительно к сигнальным микропроцессорам (СМП), которые широко используются в практике контроля и диагностики состояния сложных энергетических объектов, изначальное определение наблюдаемого свойства (диагностического параметра) означает формирование некоторой шкалы, представляющей собой совокупность отметок (делений), выбранных единиц измерений, ранжированных по правилу ψ. Эту шкалу принято называть шкалой установки метрических параметров (ШУМП). Множество измеряемых параметров зависит от типа и количества первичных преобразователей (датчиков), подключаемых к данному СМП. Вторая шкала, присущая СМП, является шкалой преобразования входного аналогового сигнала в цифровой код. Ее принято называть шкалой цифрового кодирования (ШЦК). Она учитывает дискретизацию, квантование и оцифровку входного сигнала. Третья шкала СМП является шкалой функциональных преобразований. Она может быть представлена набором шкал, количество которых зависит от числа функций данного СМП. Концептуальная модель СМП, например виброанализатора/сборщика, в состав которого, кроме функций измерения и оцифровки, входят функция быстрого преобразования Фурье, функция накопления спектров входного сигнала, измеренного в различных точках, и функция связи с технологическим компьютером, может быть представлена набором пяти шкал (рис. 2). Само собой разумеется, что СМП, реализованные в виде отдельных переносных приборов, могут иметь в своем составе еще ряд вычислительных и сервисных функций. Такими функциями могут быть: функция балансировки роторов в собственных опорах, функция установки измерительных параметров, функция занесения времени и даты замеров, функция контроля базы собранных диагностических данных и т.п. Как видно из рисунка 2, входной сигнал x(t), измеренный в соответствии с метрологическими уставками, после дискретизации, квантования и оцифровки поступает на обработку быстрым преобразованием Фурье. Далее в виде спектров S(w), измеренных во время t, он заносится в базу диагностической информации, из которой может быть извлечен и передан в технологический компьютер через промежуток времени Ti. Аналогичным образом могут быть построены концептуальные модели программных комплексов контроля и диагностики состояния (ПККДС) сложных энергетических объектов. Обычно в состав таких моделей входит три пакета шкал: шкалы управления базами данных, шкалы управления данными и шкалы анализа диагностических параметров. Не вдаваясь в подробное рассмотрение пакетов шкал управления базами данных и управления данными, рассмотрим набор шкал анализа данных. В него может входить весьма широкий набор шкал функционального преобразования диагностических параметров, количество и состав которых зависит от технологии контроля и диагностики состояния объекта, от состава контролируемых параметров и элементов контролируемых объектов. Для программного комплекса контроля и диагностики состояния, например, асинхронных агрегатов это могут быть: шкала расчета частоты скольжения, шкала определения статуса состояния объекта, функция диагностики состояния, шкала идентификации неисправностей, шкала корреляции параметров и т.д. (рис. 3). Как видно из рисунка 3, входными параметрами ПККДС технологического компьютера являются принятые из коллектора/сборщика спектры S(w), t-Ti, которые затем хранятся в базе диагностических данных технологического компьютера. Далее инженером-диагностиком может быть востребована любая из имеющихся функций, описанная шкалами пакета анализа диагностических данных. Входными параметрами таких шкал являются накопленные в базе данных спектры S(w), t-nTi на любую дату ранее выполненных замеров, число которых равно n. Выходными параметрами этих шкал являются документы в виде протоколов, номограмм, графиков и таблиц. Как правило, шкалы пакета анализа диагностических данных имеют в своем составе шкалы второго уровня, которые позволяют детализировать полученные данные первого уровня. Так, например, шкала расчета частоты скольжения (ШРЧС) имеет в своем составе шкалы аналитического и графического расчетов (на рис. 3 не показаны), которые являются шкалами второго уровня. Шкалы второго уровня самостоятельного предназначения не имеют и призваны детализировать выходные параметры (или их преобразования) шкал первого уровня. Заметим, что все шкалы, приведенные на рисунках 2 и 3, кроме двух первых шкал рисунка 2, являются полностью метрическими, то есть системы входных и выходных параметров каждой шкалы представляют собой одномерные или векторные числовые пространства. Следовательно, если определен алгоритм отображения входных параметров в выходные, то такие шкалы полностью формализованы и могут играть роль математической модели функции, которая представлена данной шкалой. Как известно из практики, определение расчетных формул или алгоритмов контроля, диагностики, распознавания неисправностей, определения частоты скольжения каких-либо технических трудностей не вызывает. Покажем это на примере построения математической модели функции диагностики состояния асинхронных агрегатов.
В зависимости от выбранной схемы оценки состояния объекта сравниваются измеренные значения контролируемых параметров с заранее установленными (заданными) предельными уровнями контролируемых параметров (рис. 4). Диагностирование состояния при трехуровневой политике распознавания сводится к сравнению измеренных параметров с их допустимыми (Фон), предельными (1ПУ) и аварийными (2ПУ) уровнями (рис. 4а). При четырехуровневой политике распознавания состояния цель диагностирования технического состояния объекта сводится к сравнению измеренных параметров с допустимыми (Фон), предельными (1ПУ), запредельными (2ПУ) и аварийными (3ПУ) уровнями (рис. 4б). При этом если определение численных значений контролируемых параметров одного замера представляет собой математическую модель состояния (статуса состояния) контролируемого объекта, то определение численных значений контролируемых параметров одного замера, превышающих значения предельных, запредельных или недопустимых уровней, представляет собой математическую модель параметрического диагноза состояния объекта. Тогда математическая модель (задачи процесса, функции) диагностирования технического состояния при трехуровневой политике распознавания состояний может быть представлена так: MmodDTsj = (Rd(t) = = P(t)
Математическую модель задачи диагностики при компьютерной обработке данных удобнее иметь не в виде аналитического выражения (4), а в форме следующего алгоритма: Yi > Fon; Yi > Fon; Yi > Fon; IS= Yi < 1PU; NI = Yi > 1PU; NR = Yi > 1PU; (5) Yi < 2PU; Yi < 2PU; Yi > 2PU, где Fon, 1PU, 2PU – численное фоновое, предельное и запредельное значения i-го диагностического параметра соответственно; IS, NI, NR – исправное, неисправное и неработоспособное состояния объекта соответственно. При этом каждый контролируемый параметр Yi принадлежит обобщенному диагностическому вектору P(t). На четвертом этапе разработки ПККДС, используя математическую модель (4) или алгоритм (5), с помощью соответствующего алгоритмического языка программирования разрабатывается программный модуль, в котором выполняется процедура диагностирования, а результат диагностирования Rd(t) представляется в виде протокола исключений или номограммы состояния с выделением параметров с предельными и/или запредельными значениями. Аналогичные исследования можно провести и для других шкал пакета анализа диагностических параметров и разработать соответствующие модули ПККДС. Совокупность всех программных модулей пакета анализа диагностических данных будет представлять собой основное ядро программного комплекса контроля и диагностики состояния наблюдаемых объектов.
Что касается содержания программных модулей, реализующих пакеты шкал управления базами данных и управления данными, то их разработка ввиду тривиальности функций трудностей не вызывает. Обычно в состав блока программных модулей управления базами данных включают модуль создания базы данных, модуль контроля активной базы данных, модуль вызова базы данных из архива и т.д., а в состав блока программных модулей управления данными включают модуль связи с прибором, модуль корректировки данных, модуль удаления из базы данных последнего замера и т.д. Список литературы 1. Кузякин В.И. Концептуальное проектирование систем мониторинга состояния оборудования буровых установок // Изв. вузов. Горный журнал.-1990. - №7. - C.94-98. 2. Кузякин В.И., Кузякин Ю.И. Концепция построения систем мониторинга технического состояния сетей ЭВМ // Тр. Международ. сем.: Территориальные информационные сети COMPAC-91.-Рига: Зинатне, 1991.-С.31-34. 3. Кузякин В.И. Методика концептуального проектирования систем технического мониторинга буровых установок // Информ. листок №91-74.-Свердловск: ЦНТИ, 1991.-4 с. 4. Арутюнов П.А. Теория и применение алгоритмических измерений.-М.: Энергоатомиздат, 1990.-256 с. 5. Баранов В.Н., Бессчастнов А.А., Богомолов В.П., Кузякин В.И. Концептуальные модели стратегий и систем технического обслуживания и ремонтов энергетических объектов. // Изв. вузов. Нефть и газ.-1998.-№6.-С.90-93. |
| Permanent link: http://swsys.ru/index.php?id=835&lang=en&page=article |
Print version Full issue in PDF (1.18Mb) |
| The article was published in issue no. № 3, 2001 |
Perhaps, you might be interested in the following articles of similar topics:
- О выборе числа процессоров в многопроцессорной вычислительной системе
- Автоматизированная информационная система маркетолога
- О программной реализации геоинформационных систем
- Сравнительный анализ некоторых алгоритмов распознавания
- Анализ российского и зарубежного рынков программных продуктов
Back to the list of articles
 Теоретические основы сложных технических систем предполагают обязательное существование концепции систем данного класса. Главными компонентами концепции системы являются цель ее создания и достигнутый или ожидаемый результат. Анализ/синтез концепции как первый этап исследования системы касается ее конструкторских, технологических, энергетических, информационных и прочих аспектов изготовления, а также климатических, экологических, организационных, производственных и других аспектов ее функционирования. Концепции сложных технических систем всегда вербальны и формализуются математическими или концептуальными и математическими моделями в зависимости от выбранного метода моделирования. В первом случае используются субъективные, или эвристические способы моделирования, а во втором – объективные или обоснованные методы построения математических моделей (рис.1).
Теоретические основы сложных технических систем предполагают обязательное существование концепции систем данного класса. Главными компонентами концепции системы являются цель ее создания и достигнутый или ожидаемый результат. Анализ/синтез концепции как первый этап исследования системы касается ее конструкторских, технологических, энергетических, информационных и прочих аспектов изготовления, а также климатических, экологических, организационных, производственных и других аспектов ее функционирования. Концепции сложных технических систем всегда вербальны и формализуются математическими или концептуальными и математическими моделями в зависимости от выбранного метода моделирования. В первом случае используются субъективные, или эвристические способы моделирования, а во втором – объективные или обоснованные методы построения математических моделей (рис.1).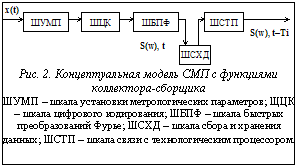 N = {M,Pj} (2)
N = {M,Pj} (2)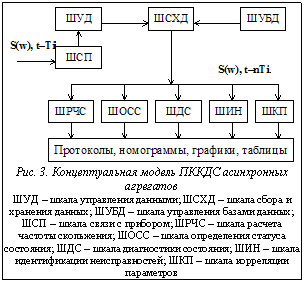 В качестве третьего этапа разработки ПККДС построим математическую модель (задачи процедуры, функции) диагностирования состояния объектов с помощью диаграмм событий/состояний. Основной функцией диагностики является распознавание состояний, в которые переходит объект в результате тех или иных событий. Процесс диагностики асинхронных агрегатов на вербальном уровне знаний рассмотрен в [5]. Обычно при построении систем диагностики технического состояния энергетических объектов возникает необходимость получать оценку текущего состояния объекта на дату любого замера контролируемых параметров (генезис состояния объекта). Решение такой задачи в общем случае проводится на базе протоколов исключений контролируемых параметров из нормы (меньше фона и больше предельного уровня). Сделать это можно только тогда, когда применяется параметрическая диагностика с использованием не менее трех уровней оценки состояний (исправен–неисправен–неработоспособен). Но наиболее продуктивной является четырехуровневая оценка состояний (исправен –неисправен –неисправен, но работоспособен –неработоспособен). При трехуровневой политике распознавания вида состояния необходим набор допустимых, предельных и аварийных уровней для всех диагностических параметров. Если речь идет о четырехуровневой политике оценки технического состоянии объекта, то уже нужно точно знать значения допустимых, предельных, запредельных и аварийных уровней диагностических параметров.
В качестве третьего этапа разработки ПККДС построим математическую модель (задачи процедуры, функции) диагностирования состояния объектов с помощью диаграмм событий/состояний. Основной функцией диагностики является распознавание состояний, в которые переходит объект в результате тех или иных событий. Процесс диагностики асинхронных агрегатов на вербальном уровне знаний рассмотрен в [5]. Обычно при построении систем диагностики технического состояния энергетических объектов возникает необходимость получать оценку текущего состояния объекта на дату любого замера контролируемых параметров (генезис состояния объекта). Решение такой задачи в общем случае проводится на базе протоколов исключений контролируемых параметров из нормы (меньше фона и больше предельного уровня). Сделать это можно только тогда, когда применяется параметрическая диагностика с использованием не менее трех уровней оценки состояний (исправен–неисправен–неработоспособен). Но наиболее продуктивной является четырехуровневая оценка состояний (исправен –неисправен –неисправен, но работоспособен –неработоспособен). При трехуровневой политике распознавания вида состояния необходим набор допустимых, предельных и аварийных уровней для всех диагностических параметров. Если речь идет о четырехуровневой политике оценки технического состоянии объекта, то уже нужно точно знать значения допустимых, предельных, запредельных и аварийных уровней диагностических параметров. (Фон, 1ПУ, 2ПУ)), (4)
(Фон, 1ПУ, 2ПУ)), (4)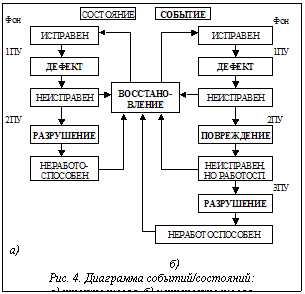 где Tsj – одно из трех возможных состояний; Rd(t) – результат диагностирования;
где Tsj – одно из трех возможных состояний; Rd(t) – результат диагностирования; 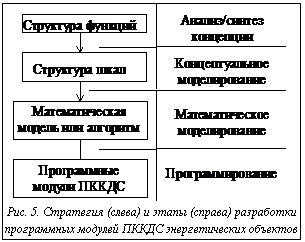 Стратегия объективного моделирования как схема последовательных целенаправленных действий и этапы разработки программных модулей ПККДС с помощью теории шкал представлены на рисунке 5.
Стратегия объективного моделирования как схема последовательных целенаправленных действий и этапы разработки программных модулей ПККДС с помощью теории шкал представлены на рисунке 5.