Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Ключевое слово: |
|
| Page views: 8831 |
Print version Full issue in PDF (2.03Mb) |
Автоматическая сборка мусора широко известна как фундаментальный механизм, освобождающий разработчиков программного обеспечения от забот по отслеживанию объема динамической памяти, занятого данными, необходимость в которых с некоторого момента отпадает. Для систем реального времени использование физической памяти является критическим фактором. Для правильной работы приложения существует необходимость точного определения ее объема, и система управления памятью должна обеспечивать использование памяти без превышения заданных ограничений. Так как практически невозможно точно предугадать, по какому сценарию будет работать система, для оценки критических ресурсов выбирают наихудший вариант их использования (worst case). В системах реального времени используется инкрементная схема исполнения сборки мусора. Прикладная задача (или набор задач) передает управление сборщику мусора на некий промежуток времени, который называется инкрементом. В течение инкремента сборщик выполняет часть своей работы, а затем возвращает управление задаче. Для выполнения полного цикла сборки (сборки мусора во всей куче), сборщику необходимо выполнить несколько инкрементов. Существует класс сборщиков мусора, использующих такую схему организации памяти, в которой отдельные блоки памяти не перемещаются во время сборки. К этому классу относятся сборщики mark-sweep и pseudo-copying [1,2]. Известно несколько вариантов выделения памяти под новые объекты в таких схемах, одной из них является простая схема хранения данных (simple segregated storage [1-3]). Основной идеей простой схемы является разбиение памяти на участки, размеры которых соответствуют объектам, используемым в приложении. Занятые блоки памяти и свободные блоки организуются в отдельные структуры. При необходимости размещения нового объекта, находится соответствующий по размеру свободный блок, и запрос на размещение удовлетворяется. В простой схеме не используется слияние смежных участков памяти для создания блоков большего размера. Рассмотрим зависимость использования памяти в системе реального времени со сборкой мусора, использующей неперемещающие сборщики с простой схемой выделения памяти. Задачей является оценка требуемой памяти в наихудшем варианте развития событий. Примем следующие обозначения:
Все умершие объекты могут стать плавающим мусором, то есть это те объекты, которые умерли после того, как сборщик уже завершил работу с ними, заместив их достижимыми. Такие блоки будут учтены на следующем цикле сборки. В течение всего цикла сборки сборщик мусора выполняет различные действия. Он осуществляет сканирование связей графа достижимости приложения, помечает живые объекты и выполняет другие действия, определяемые спецификой работы алгоритма. Часть работы сборщика мусора связана непосредственно с освобождением памяти, занимаемой неиспользуемыми объектами. В наихудшем случае стадия освобождения мусорных блоков может начинаться и заканчиваться в течение последнего инкремента цикла полной сборки в куче. При этом освобожденные блоки памяти не могут быть использованы заново на этом цикле. Объем освобожденной памяти при этом равен объему плавающего мусора, образовавшегося за предыдущий цикл сборки. В соответствии с вышесказанным, можно утверждать, что используемая системой память распределяется следующим образом: живые объекты, плавающий мусор (блоки, которые будут собираться на следующей стадии), свободные блоки. Если во время своей работы приложение использует объекты одинаковых или кратных размеров, так что все освобожденные сегменты памяти могут быть использованы заново, то фрагментация памяти отсутствует. Допустим, что после размещения На последующих циклах:
Очевидно, что для случая Таким образом, объем памяти М, используемый системой с неперемещающим сборщиком мусора, в наихудшем случае (без учета фрагментации) равен:
Величины Рассмотрим случай, когда приложение использует такие наборы объектов, что не все освобожденные блоки могут быть использованы заново (случай с фрагментацией памяти).
для для i=m+1 =>
где
Для худшего случая неравенство Таким образом, имеем:
где imin – минимальное количество полных циклов сборки мусора, до того как система будет использовать максимальный объем памяти. На рисунке 1 показан вид графиков использования памяти приложением в наихудшем случае для различных коэффициентов фрагментации. Параметры приложения условно приняты следующими: По характеру графиков можно судить о возможности работы приложения в системе со сборкой мусора в ограниченном объеме памяти. Зная предельно допустимое время работы приложения d, можно рассчитать минимальный объем памяти, который не будет превышен за все время исполнения. Как видно из рисунка 1, при проектировании системы разумно предоставлять ей количество памяти не большее, чем используется на отрезке На рисунке 2 для тех же параметров приложения построены зависимости времени работы приложения (в циклах) до использования максимального объема памяти от минимального размера используемых объектов. Следует отметить, что существуют средства борьбы с фрагментацией в неперемещающих алгоритмах, основанные на объединении смежных ячеек памяти, например, buddy systems [1-3]. Объединение блоков вносит дополнительные накладные расходы, связанные с выделением памяти, что замедляет работу приложения и может быть неприемлемо в случаях жестких ограничений систем реального времени. В заключение отметим, что оценки сборщиков мусора, основанные на предположениях о работе приложений, дают возможность проектировать системы реального времени, ориентированные на работу с прикладными задачами определенных типов. Опираясь на данные об использовании критических ресурсов, можно конфигурировать систему с учетом минимизации затрат. Имея систему с известными характеристиками, можно определить, какие приложения смогут выполняться в ней гарантированно без превышения имеющихся ресурсов. Приведенные рассуждения являются лишь частью работы по оценке наихудшего случая исполнения. Необходимо также проведение расчетов по оценке временных характеристик, зависящих как от приложений реального времени, так и от алгоритмов автоматического управления памятью. Список литературы 1. Richard Jones, Rafael Lins. Garbage collection: algorithms for automatic dynamic memory management. Chichester, England, John Wiley & Sons, 1996. 2. Mark S. Johnstone. Non-moving memory allocators and real-time garbage collection. PhD thesis, University of Texas at Austin, 1998. 3. Paul R. Wilson. Uniprocessor garbage collection techniques. Technical report, University of Texas at Austin, 1994. |
| Permanent link: http://swsys.ru/index.php?id=964&lang=en&page=article |
Print version Full issue in PDF (2.03Mb) |
| The article was published in issue no. № 4, 1999 |
Perhaps, you might be interested in the following articles of similar topics:
- Формулировка задачи планирования линейных и циклических участков кода
- Формирование программ развития больших систем административно-организационного управления
- Компьютер - хранитель домашнего очага
- Оптимизация обработки информационных запросов в СУБД
- Интеллектуальная система для моделирования затрат-потерь и распределения ресурсов по графическим образам
Back to the list of articles
 – максимальный объем памяти, занимаемый живыми (используемыми приложением) объектами;
– максимальный объем памяти, занимаемый живыми (используемыми приложением) объектами; – максимальный объем памяти, занимаемый объектами, размещаемыми приложением в течение полного цикла сборки;
– максимальный объем памяти, занимаемый объектами, размещаемыми приложением в течение полного цикла сборки; – объем памяти, ставшей неиспользуемой после исполнения i-го цикла сборки.
– объем памяти, ставшей неиспользуемой после исполнения i-го цикла сборки. . Тогда для первого цикла сборки мусора необходимый объем памяти
. Тогда для первого цикла сборки мусора необходимый объем памяти 
 . Для второго цикла сборки мусора необходимый объем памяти
. Для второго цикла сборки мусора необходимый объем памяти 
 .
. , где (i>1). (1)
, где (i>1). (1) для размещения
для размещения  , где m – количество полных циклов сборки, за время которых приложением может быть размещено
, где m – количество полных циклов сборки, за время которых приложением может быть размещено  (сколько рождается, столько и умирает).
(сколько рождается, столько и умирает). .
. Обозначим отношение объема памяти, которое не может быть использовано заново
Обозначим отношение объема памяти, которое не может быть использовано заново  , к объему свободных блоков
, к объему свободных блоков 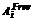 через коэффициент фрагментации
через коэффициент фрагментации  . Очевидно, что когда фрагментация отсутствует,
. Очевидно, что когда фрагментация отсутствует,  . Допустим, что для худшего случая 0больше памяти, чем требовалось на предыдущем цикле. В случае исполнения сборщиком множества циклов полной сборки неиспользуемые из-за фрагментации свободные блоки накапливаются, но часть из них может быть использована в дальнейшем. С учетом фрагментации для худшего случая использования памяти имеем:
. Допустим, что для худшего случая 0больше памяти, чем требовалось на предыдущем цикле. В случае исполнения сборщиком множества циклов полной сборки неиспользуемые из-за фрагментации свободные блоки накапливаются, но часть из них может быть использована в дальнейшем. С учетом фрагментации для худшего случая использования памяти имеем: =>
=>  ;
; ;
; (2),
(2), – объем используемой памяти на i-м цикле;
– объем используемой памяти на i-м цикле; 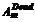 – объем памяти, занимаемой объектами, ставшими недостижимыми при i=m.
– объем памяти, занимаемой объектами, ставшими недостижимыми при i=m. При k<1 существует такое j, при котором выполняется условие
При k<1 существует такое j, при котором выполняется условие  , где
, где  – минимальный размер объектов, используемых приложением. В этом случае член
– минимальный размер объектов, используемых приложением. В этом случае член  выражения (2) теряет смысл и объем используемой памяти ограничен. Очевидно, что при k=1 количество используемой памяти никогда не ограничится (ни один блок не может быть использован заново).
выражения (2) теряет смысл и объем используемой памяти ограничен. Очевидно, что при k=1 количество используемой памяти никогда не ограничится (ни один блок не может быть использован заново). (см. (2)) может выполниться на несколько циклов раньше, чем
(см. (2)) может выполниться на несколько циклов раньше, чем  (можно показать, что разница в циклах составит
(можно показать, что разница в циклах составит  ), следовательно, число полных циклов сборки мусора до достижения максимального объема памяти будет оцениваться по члену
), следовательно, число полных циклов сборки мусора до достижения максимального объема памяти будет оцениваться по члену  .
. ,
,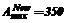 байт/цикл и
байт/цикл и  байт. Для получения абсолютного значения времени работы приложения необходимо количество циклов умножить на длительность одного цикла.
байт. Для получения абсолютного значения времени работы приложения необходимо количество циклов умножить на длительность одного цикла. , где t – время работы системы.
, где t – время работы системы.