Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: D.V. Kurennov (d.v.kurennov@urfu.ru) - Ural Federal University named after the First President of Russia B.N. Yeltsin (Associate Professor, Head of a Department of IT and Computer-Aided Design), Ekaterinburg, Russia, Ph.D, Partin A.S. (dmitriy-v-k@yandex.ru) - Institute of Engineering Science of the Ural Branch of the RAS, Ekaterinburg, Russia, Ph.D | |
| Keywords: curves and surfaces bezier, , geometrical modelling, data structure |
|
| Page views: 15125 |
Print version Full issue in PDF (4.72Mb) |
При разработке современных САПР для различных отраслей промышленности удобно использовать общее универсальное геометрическое ядро – пакет геометрического моделирования. Его функции должны обеспечить создание геометрических моделей трехмерных объектов заданной сложности, выполнение широкого спектра операций с ними, представление результатов работы в различных формах. К необходимым условиям, обеспечивающим успешное и широкое практическое применение пакета, можно отнести высокую точность вычислений, быстроту выполнения алгоритмов, надежность и стабильность в работе, а также простоту и удобство в использовании. Успешная реализация большинства перечисленных функций и требований зависит от выбранной формы представления геометрической информации в системе – структуры данных, которая изначально должна строиться на их основе и с их максимальным учетом. Требования к структуре Рассмотрим некоторые задачи геометрического моделирования применительно к проектированию структуры данных. 1. Существует необходимость точного представления объектов с неплоскими поверхностями (не многогранников), как достаточно аналитически простых (сфера, конус), так и сложных параметрических (перья турбинных лопаток, лопасти винтов и т.п.). В качестве решения предлагается использовать метод разбиения поверхности на участки и их последующего представления в виде рациональных параметрических бикубических сплайнов – порций. 2. Большую популярность приобрел способ твердотельного геометрического моделирования, в котором сложные объекты представляются составленными из простых объемных примитивов. Это достигается при помощи булевых операций объединения, вычитания, выделения общей части и т.п. Поэтому необходимо наличие в структуре данных некоторой топологической информации о взаимном расположении сплайнов, их связи друг с другом (так называемое граничное моделирование). 3. Для синтеза сложных объектов следует предварительно получить простые примитивы. Обычно к ним относят простые аналитические тела (параллелепипеды, призмы, сферы и т.п.), а также объекты, получаемые путем несложных трансформаций (тела вращения, «выдавленные» объекты и пр.), причем практика показывает, что в подавляющем большинстве случаев подобных примитивов и операций из п. 2 достаточно для представления объекта (например детали). Рассмотренная структура данных, естественно, вполне подходит для описания примитивов, однако современный уровень развития инструментальных средств САПР предусматривает, кроме того, высокий уровень интерактивности системы. Поэтому в структуре данных должна присутствовать параметрическая информация о форме и виде создаваемого объекта – радиус, линейные размеры, образующие контуры и т.п. На основе изложенного можно сделать вывод, что наиболее оптимально геометрическую модель объекта будет представлять структура данных как совокупность трех видов информации – геометрической, топологической и параметрической. В данной статье рассматриваются в основном вопросы хранения в структуре данных геометрической и топологической информации. Предлагаемая структура данных вполне допускает дальнейшее развитие и усовершенствование. Общая концепция Объект является основой структуры и предназначен для моделирования реального геометрического объекта или его части. Можно выделить следующие главные компоненты объекта. Единая поверхность. Описывает поверхность реального моделируемого объекта, является наиболее важным (но не единственным) свойством любого объекта. Тип объекта. Все многообразие существующих объектов можно разделить на отдельные типы. Это даст возможность пользователю системы строить желаемый объект не путем описания единой поверхности, очень сложной и трудоемкой для ручного описания, а путем указания на желаемый тип и его параметры – другой необходимой компоненты объекта. Целесообразно использовать иерархию типов объектов, где более «верхний» базовый объект сможет представлять все, что может более «нижний» в иерархии объект, а тот, в свою очередь, сможет представлять только некоторый подкласс геометрии «верхнего» объекта. Преимуществом иерархии является наследование объектами-потомками всех свойств-параметров их базовых объектов с добавлением к ним своих, новых, что делает ее логически упорядоченной и легко расширяемой впоследствии новыми объектами.
Описание поверхности объекта Существует необходимость описывать поверхность любого достаточно сложного объекта с возможно большей точностью и, главное, в виде единой универсальной структуры. Здесь можно выделить две основные задачи – геометрию и топологию. Геометрия: найти минимальные элементы, из которых будут составляться вся поверхность, их вид, математическое описание. Топология: задать все необходимые связи между геометрическими элементами, точно и эффективно описывающие их взаиморасположение. Рассмотрим решение этих задач в разрабатываемой версии системы. Элемент поверхности В виде минимальных элементов, задающих участки поверхности, логично использовать рациональные параметрические бикубические сплайны – порции следующего вида:
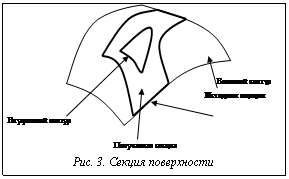
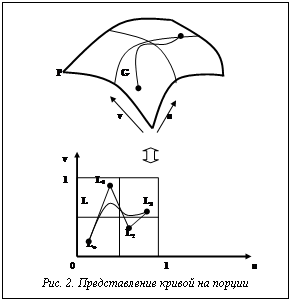
С помощью всего шестнадцати точек в однородных координатах можно получить абсолютно точные участки эллиптической, гиперболической и параболической поверхностей и, естественно, плоскости. Причем изменяться будут лишь исходные данные – точки Pij, а математический аппарат, используемый для вычисления поверхностей, останется неизменным, универсальным. Полученные порции можно соединять друг с другом по любым математически описанным критериям, допустим, с учетом непрерывности и гладкости, получая таким образом некоторую поверхность. К примеру, сферу можно составить всего из восьми порций, цилиндр – из шести. Именно такая порция и лежит в основе рассмотренного ранее понятия обобщенного цилиндра, где поверхность объекта задавалась по сути массивом M´N порций. Каждая порция имеет, естественно, не более четырех сторон, по которым она просто соединяется с четырьмя смежными ей порциями. Это самый большой недостаток данного подхода, поскольку сильно сужает класс описываемых поверхностей, в принципе ограничивая его одним лишь обобщенным цилиндром. Например, невозможно задать поверхность, получаемую при почти любом пересечении объектов (рис. 1). Видно, что указанный на рисунке элемент поверхности имеет пять (а не четыре) сторон, по которым он соединяется с другими элементами. Следовательно, для снятия данных ограничений на модель необходимо на основе классической порции создать элемент с более сложным видом (и большим числом) границ. Кривая на порции Возьмем некоторую порцию поверхности P и кривую G, точно лежащую на ней (рис. 2). Кривая состоит из множества точек поверхности P, каждая из которых имеет параметрические координаты u, v. Возьмем также плоскость в декартовой системе координат и отложим на ней точки, декартовы координаты которых совпадают с параметрическими координатами точек кривой G. Через эти точки проведем некоторую кривую L и допустим, что ее можно представить в виде рационального кубического сплайна L(t) с характеристической ломаной L0L1L2L3, где точки L0, L1, L2, L3 будут задаваться однородными координатами X, Y, H. Тогда Если теперь координаты на плоскости x и y заменить на u и v (параметрические координаты на поверхности) и задать точки L0, L1, L2, L3 однородными координатами U, V, H, то можно аналогично получить текущие параметрические координаты точки кривой:
Тогда кривая G будет отображением кривой L на поверхноcть Р:
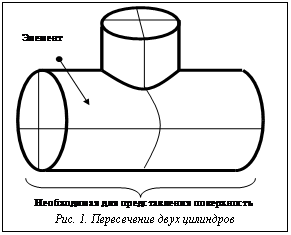
Таким образом, определен способ задания кривых – сплайнов достаточно широкого класса, заведомо точно принадлежащих какой-либо порции, через задание вершин их характеристической ломаной в параметрических координатах данной порции. Секция поверхности Для поиска необходимых элементов поверхности предлагается использовать классическую порцию поверхности и, наложив на нее некоторый контур из описанных сплайнов в параметрических координатах этой порции, вырезать из нее необходимую часть – секцию (рис. 3). В дальнейшем именно из таких элементов – секций будет строиться поверхность любого объекта в рассматриваемой структуре данных. Литература 1. Норенков И.П., Маничев В.Б. Основы теории и проектирования САПР: учеб. для вузов. М.: Высш. шк., 1990. 335 с. 2. Препарата Ф., Шеймос М. Вычислительная геометрия: введение. М.: Мир, 1989. 3. Сухих Б.И., Вайсбурд Р.А. Вычислительная геометрия. Основные объекты и преобразования: учеб. пособ. Свердловск: УПИ, 1989. 92 с. |
| Permanent link: http://swsys.ru/index.php?page=article&id=2275&lang=&lang=en&like=1 |
Print version Full issue in PDF (4.72Mb) |
| The article was published in issue no. № 2, 2009 |
Perhaps, you might be interested in the following articles of similar topics:
- Алгоритм построения гладкого сопряжения поверхностей
- Открытость структур в эволюционной модели данных
- Кривая скольжения на инструменте произвольной формы при многокоординатной обработке
- Построение кривой скольжения конического инструмента при многокоординатной обработке
- Построение траектории движения инструмента при многокоординатной обработке
Back to the list of articles
 Параметры. Каждый тип объекта имеет свои параметры, необходимые и достаточные для построения любого объекта данного типа: радиус и центр для сферы, два слагаемых объекта для объединения и т.д. В параметрах может храниться вспомогательная информация, неразрывно связанная с объектом и облегчающая работу с ним – линия пересечения для булевых комбинаций, объем и площадь для простых тел и т.д. Важно то, что объекты-потомки всегда наследуют все параметры от базовых объектов и могут добавлять к ним свои параметры, выделяющие их из класса объектов, моделируемых базовым.
Параметры. Каждый тип объекта имеет свои параметры, необходимые и достаточные для построения любого объекта данного типа: радиус и центр для сферы, два слагаемых объекта для объединения и т.д. В параметрах может храниться вспомогательная информация, неразрывно связанная с объектом и облегчающая работу с ним – линия пересечения для булевых комбинаций, объем и площадь для простых тел и т.д. Важно то, что объекты-потомки всегда наследуют все параметры от базовых объектов и могут добавлять к ним свои параметры, выделяющие их из класса объектов, моделируемых базовым.
 ,
,  .
. ,
, 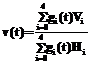 .
. .
.