Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Оптимальная энтропийная кластеризация в информационных системах
Аннотация:В данной работе исследована возможность разработки нового метода кластеризации данных в информационных системах. Кластеризация – это процесс нахождения возможных групп в заданном множестве с учетом признаков схожести или различия элементов этого множества. Существующий метод энтропийной кластеризации представляет собой информационно-теоретический подход к задаче кластеризации. В статье предлагается метод оптимальной энтропийной кластеризации высокоразмерных данных в информационных системах, который базируется на энтропийном подходе к выбору состояния элементов сообщений. Дано его математическое обоснование. Разработанный метод оптимальной энтропийной кластеризации базируется на известном принципе «малая величина энтропии соответствует большому количеству информационного содержания» и позволяет формировать режим не только оптимальной кластеризации, но и сокращения признакового пространства. Предложены методики вычисления степени оптимальности проведенной кластеризации, а также сокращения признакового пространства высокоразмерных данных при их первичной обработке.
Abstract:The paper researches the possibility of developing a new method for data clustering in information systems. Clustering is a process of searching possible groups in a given set using signs of similarity or difference between elements of this set. The existing entropy clustering method includes an information theoretic approach to a clustering task. The paper suggests a clustering method based on an entropy approach to selecting message items. The paper suggests a method of optimum entropy clustering of high-dimensional data in information systems. It also gives mathematical grounding of the method. The suggested method of optimum entropy clustering is based on the known principle “low entropy corresponds to big information content”. This make it possible to form an optimum clustering regime, as well as an attribute space reduction regime. The paper proposes a method for calculating a level of clustering optimality. It also describes a method for reducting attribute space of high-dimensional data upon their initial processing.
| Авторы: Аскерова Б.Г. (Bahar287@mail.ru) - Азербайджанский государственный университет нефти и промышленности (доцент), Баку, Азербайджан, кандидат технических наук | |
| Ключевые слова: энтропия, информационные системы, высокоразмерные данные, оптимизация, кластеризация |
|
| Keywords: entropy, information systems, high-dimensional data, optimisation, clusterization |
|
| Количество просмотров: 8586 |
Статья в формате PDF Выпуск в формате PDF (29.80Мб) |
Кластеризация объектов сложной природы с высокой размерностью признакового пространства является актуальной задачей во многих областях научных исследований [1–5]. Среди методов сокращения размерности пространства признаков в качестве основных выделяются методы главных компонент и нормализации [1]. Первый из указанных методов чересчур чувствителен к методам предобработки данных, а второй требует обоснованного выбора метода нормализации высокоразмерных данных. Согласно [1], важной и актуальной задачей является разработка эффективных методов предобработки данных и сокращения размерности признакового пространства без существенной потери информации. Кластеризация – это процесс нахождения различных групп в заданном множестве с учетом признаков схожести или различия элементов этого множества [3]. При этом в качестве меры схожести или различия используют метрику в виде расстояния между векторами x и y:
где xi, yi – i-я координата векторов x, y, В работе [4] кластеризация представляется как первичный анализ большого объема данных высокой размерности при отсутствии априорных знаний о них. В методе SEC [4] кластеры организуются по признаку эффективности сжатия бинарных векторов при использовании отдельного кодера для каждой группы. В работе [5] решена задача подбора признака для кластеризации на основе количественной характеристики, вырабатываемой с помощью четырех предложенных алгоритмов классификации. При этом подбор признака осуществляется методом, позволяющим определить подмножества исходных признаков, имеющих одинаковую смысловую информацию в отношении БД. Качественная предобработка признаков объекта может быть осуществлена по методу энтропии, используя условие минимума энтропии Шеннона, что соответствует максимальной информации об изучаемых объектах [1, 6, 7]. Что касается практической пользы кластеризации, то, например, согласно [2, 8], она помогает идентифицировать группы генов, имеющих сходные образы экспрессии при различных условиях. Такие гены типичным образом вовлечены в выполнение связанных функций. В работе [2] предлагается информационно-теоретический подход к кластеризации данных экспрессии генов. Известно, что энтропия является мерой информации и неопределенности случайного переменного. Следовательно, критерием кластеризации может стать условие достижения минимума энтропии. При использовании критерия минимальной энтропии проблема кластеризации имеет две субпроблемы: оценка a posteriori вероятности и минимизация энтропии. При этом, так как энтропия является мерой беспорядка в системе, каждый кластер должен иметь минимальную энтропию. Другими словами, данные в одном и том же кластере должны иметь схожие числовые характеристики. Существующий метод энтро- пийной кластеризации представляет собой информационно-теоретический подход к задаче кластеризации. Например, в простом случае каждый отдельный кластер должен содержать объекты с одинаковой величиной энтропии [9, 10], однако су- ществующий метод энтропийной кластеризации может быть подкреплен известным принципом «малая величина энтропии соответствует большому количеству информационного содержания». Учет данного принципа позволяет по-новому подойти к методу энтропийной кластеризации и в сущности разработать новый метод оптимальной энтропийной кластеризации. Предлагаемый метод оптимальной энтропийной кластеризации Предлагаемый в настоящей статье метод кластеризации базируется на энтропийном подходе к выбору состояния элементов сообщения. Допустим, имеется множество Х независимых элементов хi, При этом формируются кластеры K(Pj), Порядок формирования кластеров такой, что в кластер K(Pj) включаются элементы, имеющие Pj состояний. Если обозначить количество элементов в каждом j-м кластере как nj, то общее количество информации, содержащейся во всех элементах одного j-го кластера, вычислим как
Суммируя (1) по всем j, получим
Далее допустим существование функциональной связи между переменными nj и Pj, то есть
Также допускается существование определенного ограничения на сумму
Кластеризацию элементов xi по предлагаемому информационно-вариационному критерию будем считать оптимальной, если при вычисленной оптимальной функции φ(n)opt общее количество информации, определяемое выражением
где λ – множитель Лагранжа, с учетом условия (4) достигает максимальной величины. Для оценки степени оптимальности реальной кластеризации введем на рассмотрение коэффициент оптимальности, определяемый как
где φ(nj)real – реальная функция зависимости Pi от количества элементов nj в кластере Pj. Покажем порядок вычисления оптимальной функции φ(nj). Выражение (5) в условно-непрерывном виде может быть записано следующим образом:
при где C = const. Согласно уравнению Эйлера [11], оптимальная функция φ(n)opt, приводящая функционал (7) к его экстремальному значению, должна удовлетворить условию
С учетом выражений (7) и (8) получаем
Из выражения (10) находим
С учетом выражений (8) и (11) получаем
Из выражения (12) получим
С учетом выражений (10) и (13) получаем
Таким образом, при оптимальной функции φ(n)opt, определяемой выражением (14), информационное содержание идеально кластерированного множества Х, определяемое выражением (7), достигает экстремума. При этом экстремум является максимумом, так как выражение
имеет отрицательное значение. Сокращение признакового пространства Как видно из выражения (14), оптимальная функция φ(n)opt зависит от переменного n и от параметра С, исходно задаваемого при решении задачи оптимальной кластеризации. Рассмотрим возможность сокращения признакового пространства в предложенном методе кластеризации. Предлагается следующий алгоритм сокращения признакового пространства. 1. Определяется максимальная величина функ- ционала:
С учетом выражений (14) и (16) имеем
2. Определяется реальная величина функционала (16). С учетом выражения (16) и φ=φ(n)real получаем
3. Критерий сокращения признакового пространства имеет вид Принимается, что по достижении условия β ≥ a0, где a0 – заранее заданное число, a0 ≤ 1, элементы xi с количеством состояний, определяющих величину F1.H.1.real, могут быть исключены из рассмотрения. Заключение Таким образом, предлагаемый метод оптимальной энтропийной кластеризации, базируясь на известном принципе «малая величина энтропии соответствует большому количеству информационного содержания», позволяет формировать режим не только оптимальной кластеризации, но и сокращения признакового пространства. Предлагаемый алгоритм может быть реализован в среде MATLAB методом последовательных приближений. Преимуществом среды MATLAB является возможность быстрой по сравнению с ФОРТРАН разработки рабочего алгоритма, а также альтернативных решений с использованием существующего пакета программ в этой среде. Таким образом, были предложены метод опти- мальной энтропийной кластеризации высокоразмерных данных в информационных системах с его математическим обоснованием, а также методика сокращения признакового пространства высокоразмерных данных при первичной обработке. Литература 1. Бабичев С.А. Оптимизация процесса предобработки информации в системах кластеризации высокоразмерных данных // Radioelektronika, informatika, управлiння. 2014. № 2. С. 135–142. 2. Li H., Zhang K., Jiang T. Minimum entropy clustering and applications to gene expression analysis. URL: https://www.ncbi. nlm.nih.gov/pubmed/16448008 (дата обращения: 30.03.2017). 3. Santos J.M., Sa J.M., Alexandre L.A. LEGClust – a clustering algorithm based on layered entropic subgraphs. IEEE Transactions on pattern analysis and machine intelligence, 2008, vol. 30, no. 1, pp. 1–13. 4. Smieja M., Nakoneczny S., Tabor J. Fast entropy clustering in sparse high dimensional binary data. URL: http://ww2.ii.uj.edu. pl/~smieja/publications/SEC.pdf (дата обращения: 30.03.2017). 5. Singh B., Kushwaha N., Vyas O.P. A feature subset selection technique for high dimensional data using symmetric uncertainty. Jour. of Data Analysis and Information Processing, 2014, no. 2, pp. 95–105. 6. Выбор компонентов (интеллектуальный анализ данных). URL: http://msdn.microsoft.com/ru-ru/library/ms175382 (d=printer).aspx (дата обращения: 30.03.2017). 7. Zimmermann A. Objectively evaluating interestingness measures for frequent item set mining. URL: http://zimmermanna. users.greyc.fr/papers/international-workshops/pakdd2013objectively-evaluating.pdf (дата обращения: 30.03.2017). 8. Sahar S. What is interesting: studies on interestingness in knowledge discovery. URL: http://www.cs.tau.acil/~mansour/students/SigalSaharPhD.pdf (дата обращения: 30.03.2017). 9. Tew C., Giraud-Carrier C., Tanner K., Burton S. Behavior – based clustering and analysis of interestingness measures for association rule mining. URL: http://dml.cs.byu.edu/~cgc/docs/mldm_ tools/Slides/10.1--7_s10618-013-0326-x.pdf (дата обращения: 30.03.2017). 10. Malik H.H., Kender J.R. Instance Driven Hierarchical Clustering of Document Collections. URL: http://www.ke.tu-darmstadt. de/events/LeGo-08/8.pdf (дата обращения: 30.03.2017). 11. Эльцгольц Л.П. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1974. 432 с. References
|
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4360 |
Статья в формате PDF Выпуск в формате PDF (29.80Мб) |
| Статья опубликована в выпуске журнала № 4 за 2017 год. [ на стр. 643-646 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Метод выбора оптимальной технологии строительства коммуникационного тоннеля
- Система реконструкции моделей материалов по фотоизображениям
- Разработка метода интеграции информационных систем на основе метамоделирования и онтологии предметной области
- Об одном подходе к реализации облачных услуг на основе модели EaaS
- Программная система реструктуризации группы предприятий электроэнергетики
Назад, к списку статей



 ,
,  wi – i-й весовой коэффициент. При w = 1 выражение представляет собой расстояние Минковского порядка p, при p = 2 получаем расстояние Эвклида, при p = 1 – расстояние Манхеттена, при l = ∞ – расстояние Чебышева.
wi – i-й весовой коэффициент. При w = 1 выражение представляет собой расстояние Минковского порядка p, при p = 2 получаем расстояние Эвклида, при p = 1 – расстояние Манхеттена, при l = ∞ – расстояние Чебышева. , то есть X = {xi}.
, то есть X = {xi}. .
. . (1)
. (1) . (2)
. (2) . (3)
. (3) , то есть
, то есть
 где C = const. (4)
где C = const. (4) , (5)
, (5) , (6)
, (6) (7)
(7) (8)
(8) . (9)
. (9) . (10)
. (10) . (11)
. (11) . (12)
. (12) . (13)
. (13) . (14)
. (14)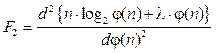 (15)
(15) . (16)
. (16)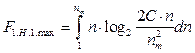 . (17)
. (17) . (18)
. (18) .
.