В различных прикладных областях науки и производства часто возникают задачи кластеризации данных. Основной целью при их решении является разбиение совокупности объектов, определяемых всевозможными характеристиками, на максимально различные группы – кластеры, содержащие максимально похожие объекты. Одной из важных проблем в этих задачах является качество получаемых кластерных решений, которое принято определять через значения критериев.
Использование разных критериев может приводить к различным конечным результатам, но практическая оценка влияния этих критериев изучена недостаточно подробно. Рассмотрим решения задачи кластеризации на практическом примере двумя различными методами.
Данная задача многофакторного анализа и выделения сегмента преподавателей-новаторов решалась в рамках выполнения Национального проекта «Образование» в 2006 г. по программе «Совершенствование системы повышения квалификации и профессиональной переподготовки педагогических, инженерно-технических кадров общеобразовательных школ в области информационных и коммуникационных технологий (ИКТ) и смежных областей». Была собрана и обработана информация по использованию ИКТ в профессиональной деятельности среди 5 500 участников программы из семи федеральных округов, прошедших в 2006 г. повышение квалификации. Рассматриваемая выборка содержит оценки 595 респондентами 25 утверждений психологического характера по 4-балльной шкале согласия Лайкерта. На первом шаге исследования была сокращена размерность задачи за счет параметров, характеризующих респондентов.
Методом главных осей из раздела факторного анализа удалось сгруппировать упомянутые 25 утверждений в 10 факторов (см. табл.), при этом значения полученных факторов были приведены к исходной шкале методом ранжирования по квартилям. Для последующего кластерного анализа проинтерпретированы значения факторов и рассчитаны факторные рейтинги по регрессионной модели. Соответствующие расчеты проделаны в пакете статистической обработки данных SPSS версии 13.0.
В процессе исследования рассмотрены кластерные решения, полученные методом k-средних для различного числа кластеров, в интервале от двух до двадцати кластеров. Для каждого кластерного решения были вычислены значения нескольких критериев качества, характеризующих дисперсию объектов в кластерах, и их арифметические комбинации – отношения. Выбранные критерии достаточно часто применяются в приложениях и удачно характеризуют пространственную структуру задачи – компактность кластеров и их удаленность друг от друга.
Факторы, полученные по исходным высказываниям
|
Фактор
|
Описание
|
|
Ф1
|
Высокая ответственность, стремление планировать
|
|
Ф2
|
Склонность к новаторству, стремление учить других
|
|
Ф3
|
Неуверенность в себе, проблемы с общением
|
|
Ф4
|
Склонность к авантюрам, карьеризм
|
|
Ф5
|
Удовлетворение своей работой
|
|
Ф6
|
Высокая самооценка, желание зарабатывать больше
|
|
Ф7
|
Желание сменить профессию
|
|
Ф8
|
Ответственное отношение к любой работе
|
|
Ф9
|
Работа по необходимости
|
|
Ф10
|
Простое отношение к деньгам
|
В качестве этих критериев выбраны средние межкластерное и внутрикластерное расстояния (Q1 и Q2), а также суммы квадратов межкластерных и внутрикластерных расстояний (Q3 и Q4). Для нахождения наиболее приемлемого решения было вычислено также отношение внутрикластерного расстояния к межкластерному (Q5 и Q6), которое необходимо минимизировать для получения локального оптимума. Приведем конкретные вычислительные формулы для этих критериев [1]:
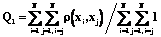 ; (1)
; (1)
 ; (2)
; (2)
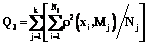 ; (3)
; (3)
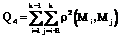 ; (4)
; (4)
 ; (5)
; (5)
 , (6)
, (6)
 где ρ(xi, xj) – евклидово расстояние между объектами xi и xj; N – число объектов; k – число кластеров; Mi и Mj – центры тяжести кластеров i и j.
где ρ(xi, xj) – евклидово расстояние между объектами xi и xj; N – число объектов; k – число кластеров; Mi и Mj – центры тяжести кластеров i и j.
Проведенные практические исследования показали, что среднее межкластерное расстояние Q1 и среднее внутрикластерное расстояние Q2 уменьшаются с ростом числа кластеров с разной скоростью. При этом четко выраженный оптимум не достигается ни по одному из критериев, если отбросить решения для крайних значений числа кластеров – двух и двадцати. В окрестности этих значений есть малые изменения (менее 1 %) межкластерного расстояния. Таким образом, приемлемое кластерное решение можно выбирать, исходя из минимума внутрикластерного расстояния, для 14–20 кластеров.
При рассмотрении пары критериев Q3 и Q4 возникает аналогичная ситуация. Критерии для данных решений не имеют выраженных локальных оптимумов, поэтому приемлемые решения приходится искать только при одновременном учете обоих критериев. При этом сумма квадратов Q4 растет линейно, а критерий Q3 – квадратично при увеличении числа кластеров. В данном случае наблюдается сравнительная фиксация внутрикластерного критерия Q3 на участке 16–20 кластеров (изменения не более 5 %) при резком увеличении межкластерного критерия Q4.
Для проверки сделанных предположений построены графики отношений внутрикластерного критерия к межкластерному в каждой рассмотренной паре соответственно: Q1 и Q2, Q3 и Q4. Для усредненных критериев было получено слабое, почти линейное изменение, а для сумм квадратов – резкая зависимость, подобная гиперболической. Полученные минимальные значения обеих комбинаций критериев Q5 и Q6 лежат в области 14–20 кластеров.
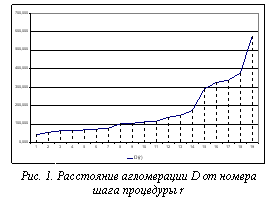
Рассматриваемая задача решалась также с помощью метода карманной кластеризации [2] при следующих значениях параметров: число подвыборок l=10, число кластеров в подвыборках k=5. В качестве способа измерения расстояния между объектами выбрано также евклидово расстояние. Рассчитаем значения тех же критериев Q1, Q2, Q3, Q4, Q5, Q6 для решений от 2 до 20 кластеров. Дополнительно к графикам изменения критериев построим график расстояния агломерации для тех же решений, чтобы определить оптимальное число кластеров по формуле для иерархических методов: N–r+1, где N – число объектов; r – шаг скачка расстояния агломерации [3].
Для метода карманной кластеризации критерий Q¢1 имеет локальный максимум для решения из трех кластеров, причем это значение больше аналогичного значения Q1 для метода k-средних. Значение критерия Q¢2 снижается с ростом числа кластеров медленнее, чем Q2 для метода k-средних, и оптимальное значение достигается только на границе из 20 кластеров. Исходя из сравнения этих графиков с предыдущими, можно сделать вывод, что решения методом карманной кластеризации по внутрикластерному расстоянию хуже, чем по методу k-средних, и наоборот, лучше по межкластерному расстоянию. Таким образом, кластеры, получаемые авторским методом, более отличаются друг от друга, но менее компактны.
 Для метода карманной кластеризации сумма квадратов межкластерных расстояний Q¢3 растет быстрее для решений из небольшого числа кластеров, чем та же сумма для решений метода k-средних. Сумма квадратов внутрикластерного расстояния Q¢4 для начальных решений авторского метода растет медленнее аналогичной суммы второго метода. Отсюда следует, что решения по методу карманной кластеризации с небольшим числом кластеров являются более оптимальными, чем решения методом k-средних, а для многокластерных решений ситуация меняется противоположным образом.
Для метода карманной кластеризации сумма квадратов межкластерных расстояний Q¢3 растет быстрее для решений из небольшого числа кластеров, чем та же сумма для решений метода k-средних. Сумма квадратов внутрикластерного расстояния Q¢4 для начальных решений авторского метода растет медленнее аналогичной суммы второго метода. Отсюда следует, что решения по методу карманной кластеризации с небольшим числом кластеров являются более оптимальными, чем решения методом k-средних, а для многокластерных решений ситуация меняется противоположным образом.
Изменения отношений Q5 и Q6 в зависимости от числа кластеров похожи для обоих методов, однако отношение усредненных функционалов для метода k-средних ближе к оптимуму (минимуму) по своим значениям, чем для метода карманной кластеризации. Значения отношения квадратичных сумм, напротив, находятся ближе к максимуму в случае второго метода. Среднее отличие значений Q5 и Q¢5 достаточно небольшое и составляет 10,7 %. Среднее отличие Q6 и Q¢6 составляет 23,9 %. Отличие для решений небольшого числа кластеров равно 5,3 % и 42,7 %. Отсюда следует, что решения по методу карманной кластеризации значительно более близки оптимуму при одновременном учете внутрикластерного и межкластерного критериев в виде суммы квадратов.
С помощью графика расстояния агломерации определим оптимальное число кластеров (рис. 1) по числу шагов процедуры объединения. Первый значительный скачок соответствует 15-му шагу и, соответственно, решению из 6 кластеров. Относительный размер скачка расстояния D составляет при этом 67,2 %.
Найденное таким образом решение для метода карманной кластеризации оказывается ближе к оптимуму, чем аналогичное решение из 6 кластеров для метода k-средних. Сравнивая решения для разных кластерных методов (рис. 2), можно убедиться, что кластеры, создаваемые методом k-средних, имеют более равномерно распределенный объем из-за особенностей алгоритмической схемы. Однако небольшой размер двух кластеров (4 % и 5 %) может указывать на большую точность авторского метода в качественном, практическом смысле.
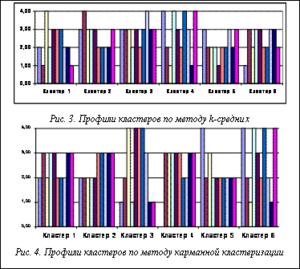 Для выяснения практической разницы между обоими кластерными решениями были построены профили кластеров по значениям факторов (см. рис. 3–4, факторы приводятся в соответствии с табл.). Чтобы оценить конкретную, практически значимую разницу между этими вариантами, был исследован так называемый кластер инноваторов – учителей, которые внедряют новые методики обучения на основе ИКТ, используют различные технические и программные средства при проведении занятий, а также обучают коллег использованию ИКТ.
Для выяснения практической разницы между обоими кластерными решениями были построены профили кластеров по значениям факторов (см. рис. 3–4, факторы приводятся в соответствии с табл.). Чтобы оценить конкретную, практически значимую разницу между этими вариантами, был исследован так называемый кластер инноваторов – учителей, которые внедряют новые методики обучения на основе ИКТ, используют различные технические и программные средства при проведении занятий, а также обучают коллег использованию ИКТ.
С точки зрения психологии инноваторы определяются как минимум согласием со вторым фактором и несогласием с третьим, то есть они должны иметь склонность к новаторству и не испытывать проблем с общением с другими людьми.В решении по методу k-средних имеется только один кластер, удовлетворяющий указанным условиям, – первый. Для решения по методу карманной кластеризации таких сегментов уже два – третий и пятый. В количественном отношении первый кластер приблизительно равен сумме третьего и пятого, качественно его профиль близок к профилю третьего кластера.
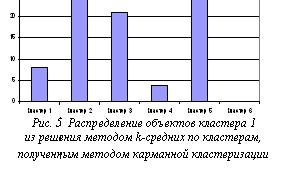 Первый кластер содержит целиком третий (21 объект) и более половины пятого (рис. 5) кластера (30 объектов). Таким образом, карманная кластеризация более точно разграничила два типа инноваторов, что было проверено с помощью построения профилей по дополнительным вопросам исследования.
Первый кластер содержит целиком третий (21 объект) и более половины пятого (рис. 5) кластера (30 объектов). Таким образом, карманная кластеризация более точно разграничила два типа инноваторов, что было проверено с помощью построения профилей по дополнительным вопросам исследования.
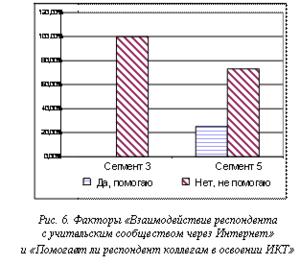
Так, респонденты из третьего кластера на практике не применяют ИКТ и не помогают коллегам в их освоении (рис. 6), значит, в действительности они не являются инноваторами. Отсюда следует, что решение по методу k-средних содержит неверные сведения и как минимум 21 человек попал в искомый сегмент по ошибке. По результатам проведенного исследования планировалось выделение авторских грантов, поэтому выбор неверного решения мог привести к негативным общественным последствиям.
В заключение можно отметить, что метод карманной кластеризации в данном случае оказался более эффективным, чем традиционный метод k-средних, так как он не требовал многократных расчетов для различных кластерных решений. Также было показано, что качество решения авторским методом в смысле Q6 оказалось выше, чем при первом методе. Практическая оценка качества кластеризации, проведенная с помощью профилирования полученных кластеров по вопросам исследования и интерпретации полученных результатов, показала, что с помощью метода k-средних был получен неверный состав объектов в целевом сегменте инноваторов.
Литература
1. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы: учебник. М.: Финансы и статистика, 2003.
2. Киреев В.С., Синицын С.В. Оптимальность кластерных решений, получаемых методом «карманной кластеризации» // Современные технологии в задачах управления, автоматики и обработки информации: тр. XVI Междунар. науч.-технич. сем. Алушта, 2007. С. 58.
3. Айвазян С.А., Мхитарян В.С. Прикладная статистика. Основы эконометрики: учебник для вузов: в 2 т. Т. 1: Теория вероятностей и прикладная статистика. М.: ЮНИТИА-ДАНА, 2001.



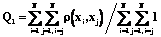 ; (1)
; (1) ; (2)
; (2)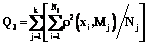 ; (3)
; (3)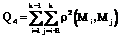 ; (4)
; (4) ; (5)
; (5) , (6)
, (6) где ρ(xi, xj) – евклидово расстояние между объектами xi и xj; N – число объектов; k – число кластеров; Mi и Mj – центры тяжести кластеров i и j.
где ρ(xi, xj) – евклидово расстояние между объектами xi и xj; N – число объектов; k – число кластеров; Mi и Mj – центры тяжести кластеров i и j. Для метода карманной кластеризации сумма квадратов межкластерных расстояний Q¢3 растет быстрее для решений из небольшого числа кластеров, чем та же сумма для решений метода k-средних. Сумма квадратов внутрикластерного расстояния Q¢4 для начальных решений авторского метода растет медленнее аналогичной суммы второго метода. Отсюда следует, что решения по методу карманной кластеризации с небольшим числом кластеров являются более оптимальными, чем решения методом k-средних, а для многокластерных решений ситуация меняется противоположным образом.
Для метода карманной кластеризации сумма квадратов межкластерных расстояний Q¢3 растет быстрее для решений из небольшого числа кластеров, чем та же сумма для решений метода k-средних. Сумма квадратов внутрикластерного расстояния Q¢4 для начальных решений авторского метода растет медленнее аналогичной суммы второго метода. Отсюда следует, что решения по методу карманной кластеризации с небольшим числом кластеров являются более оптимальными, чем решения методом k-средних, а для многокластерных решений ситуация меняется противоположным образом.


