Инновационный и модернизационный пути развития экономики делают актуальным решение ряда задач, связанных с инновационной деятельностью (ИД). Одной из них является задача планирования ИД, решение которой – план ИД – это список инновационных модернизационных мероприятий (ИММ), реализуемых тем или иным способом. Инновационной назовем деятельность по созданию и реализации новации. При этом под новацией будем понимать новое знание, которое может быть внедрено в практику и использовано, а под инновацией – новацию, внедренную в практику. В работе [1] описаны особенности планируемой инновационной деятельности и показано, что задачу следует ставить и решать как оптимизационную задачу распределения ресурсов на графовых моделях. Для ее решения были введены новые показатели оценивания качества ИД на основе инновационного потенциала [2] модернизируемой производственной системы (МПрС). А именно, под целевым результатом ИД в задаче понимается улучшение эффектов модернизируемой производственной деятельности (МПД). МПД протекает в виде функционирования МПрС для достижения ею возможных целей. Улучшение эффектов МПД оценивается по показателям, характеризующим спектр процессов, соответствующих разным возможным целям функционирования МПрС. Качество функционирования МПрС оценивают по эффективности ее функционирования, то есть по свойству целенаправленного процесса функционирования системы (МПрС), характеризующему приспособленность функционирования системы к достижению заданной цели [3]. Свойство системы (МПрС), позволяющее использовать ее для достижения любой из возможных целей, назовем потенциалом системы (МПрС). Инновационный потенциал системы – потенциал системы, получаемый в результате ИД. Задача планирования ИД состоит в следующем.
Пусть заданы: ИММ, которые могут быть включены в план ИД; возможные способы реализации ИММ и прогнозируемые результаты ИММ (возможные затраты денежных средств и времени на производственные мероприятия) для каждого способа реализации; графики МПД; ресурсы, которые могут быть израсходованы при инновационной и производственной деятельности.
Требуется найти оптимальный план ИД. При этом под оптимальным следует понимать такой план ИД, который позволит добиться лучшего значения показателя качества инновационной и производственной деятельности в процессе достижения возможных целей МПрС. Этот показатель – мера возможности того, что после завершения ИД будут получены требуемые целевые результаты функционирования МПрС и при этом не перерасходуются ресурсы, предоставленные для реализации ИД и МПД.
Введем следующие обозначения: Mi – i-е ИММ; 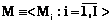 ;
;  – это Mi при pi-м способе его реализации,
– это Mi при pi-м способе его реализации, 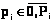 : pi=0, если
: pi=0, если  не реализуется;
не реализуется; 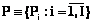 ;
; 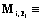
 ;
; 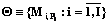 ;
; 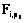 – вектор характеристик способа реализации
– вектор характеристик способа реализации  ;
; 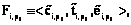 где
где 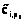 – случайная величина материальных затрат на реализацию
– случайная величина материальных затрат на реализацию  ,
, 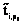 – случайная величина длительности
– случайная величина длительности  ,
,  – размер множества
– размер множества 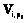 мероприятий МПД, затронутых реализацией
мероприятий МПД, затронутых реализацией  ,
, 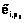 – вектор эффектов каждого мероприятия Vl МПД:
– вектор эффектов каждого мероприятия Vl МПД: 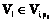 ;
;  ;
;  – вектор случайных величин эффектов l-го мероприятия МПД при выполнении
– вектор случайных величин эффектов l-го мероприятия МПД при выполнении  ;
; 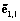 – случайная величина материальных затрат на реализацию такого мероприятия;
– случайная величина материальных затрат на реализацию такого мероприятия; 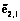 – случайная величина временных затрат на его реализацию;
– случайная величина временных затрат на его реализацию; 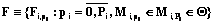 ;
; 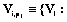
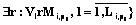 ; r – отношение зависимости между мероприятиями Vl и
; r – отношение зависимости между мероприятиями Vl и  ;
;  ;
; 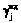 – сетевой график МПД для достижения j-й цели Gj,
– сетевой график МПД для достижения j-й цели Gj,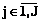 ;
; 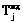 – вектор плановых моментов времени начала МПД по графику
– вектор плановых моментов времени начала МПД по графику 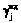 ;
; 
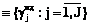 ;
; 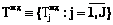 ;
; 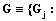
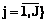 ;
;  – s-й план ИД из множества P возможных планов: psÎP;
– s-й план ИД из множества P возможных планов: psÎP; 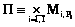 ; popt – оптимальный план ИД; W(ps) – показатель качества инновационной и производственной деятельности при плане ps;
; popt – оптимальный план ИД; W(ps) – показатель качества инновационной и производственной деятельности при плане ps; 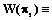

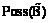 – мера возможности наступления случайного события
– мера возможности наступления случайного события  ;
; 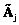 – событие, состоящее в актуализации цели Gj;
– событие, состоящее в актуализации цели Gj;  – случайный момент времени окончания МПД в соответствии с
– случайный момент времени окончания МПД в соответствии с 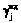 при плане ps;
при плане ps; 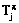 – директивный (требуемый) момент окончания МПД в соответствии с
– директивный (требуемый) момент окончания МПД в соответствии с 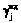 ;
;  ;
;  – случайная сумма денежных средств, расходуемых на ИММ и МПД в соответствии с планом ps для достижения цели Gj;
– случайная сумма денежных средств, расходуемых на ИММ и МПД в соответствии с планом ps для достижения цели Gj; 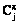 – директивная (назначенная) сумма денежных средств, выделенных на ИММ и МПД для достижения цели Gj;
– директивная (назначенная) сумма денежных средств, выделенных на ИММ и МПД для достижения цели Gj; 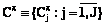 ;
; 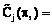
 ,
, 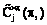 – сумма денежных средств, расходуемых на реализацию ИД в соответствии с планом ps для достижения цели Gj;
– сумма денежных средств, расходуемых на реализацию ИД в соответствии с планом ps для достижения цели Gj; 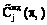 – сумма денежных средств, расходуемых на реализацию МД по графику
– сумма денежных средств, расходуемых на реализацию МД по графику 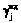 при плане ps;
при плане ps;  . Тогда решаемая задача примет следующий вид.
. Тогда решаемая задача примет следующий вид.
Дано: M, R, Q, F, V, Гмл, Tмл, G, Tд, Сд, П, r.
Найти popt: 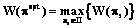 .
.
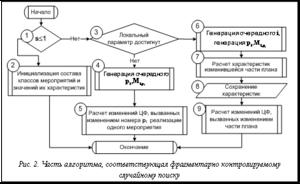
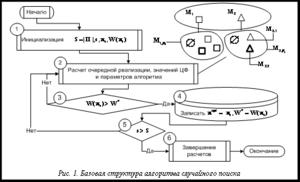 Для расчета значения W(ps) при плане ps принимается, что получение требуемых целевых результатов мероприятий МПД – событие достоверное, и используется расширенная графовая модель, помеченная нечеткими величинами – нецелевыми результатами отдельных мероприятий, входящих в ИД и в МПД [4]. Это позволяет рассчитать значение W(ps) путем обходов соответствующего графа и выполнения при этом операций алгебры нечетких чисел [5] в его узлах. Полученные в итоге рекуррентные алгебраические соотношения позволяют перейти к поиску решения оптимизационной задачи. Он выполняется с использованием модифицированного метода случайного поиска, базовая структура алгоритма которого показана на рисунке 1. Предложенная модификация – фрагментарно контролируемый случайный поиск – показана на рисунке 2. В ней используются две особенности множества выбора, проиллюстрированные в верхней части рисунка 1 для I=2, P1=3, P2=2. А именно, для пары последовательно генерируемых планов, например p1 и p2, отличающихся номерами способа реализа- ции лишь одного мероприятия (например, мероприятия M2, обозначенного треугольником), пара рекуррентных соотношений для расчета W(p1) и W(p2) содержит общие части, соответствующие общим частям планов p1 и p2. Это дает возможность сократить вычисления для W(p2) после вычисления W(p1) (блоки 4–5 и блоки 6–9 на рис. 2).
Для расчета значения W(ps) при плане ps принимается, что получение требуемых целевых результатов мероприятий МПД – событие достоверное, и используется расширенная графовая модель, помеченная нечеткими величинами – нецелевыми результатами отдельных мероприятий, входящих в ИД и в МПД [4]. Это позволяет рассчитать значение W(ps) путем обходов соответствующего графа и выполнения при этом операций алгебры нечетких чисел [5] в его узлах. Полученные в итоге рекуррентные алгебраические соотношения позволяют перейти к поиску решения оптимизационной задачи. Он выполняется с использованием модифицированного метода случайного поиска, базовая структура алгоритма которого показана на рисунке 1. Предложенная модификация – фрагментарно контролируемый случайный поиск – показана на рисунке 2. В ней используются две особенности множества выбора, проиллюстрированные в верхней части рисунка 1 для I=2, P1=3, P2=2. А именно, для пары последовательно генерируемых планов, например p1 и p2, отличающихся номерами способа реализа- ции лишь одного мероприятия (например, мероприятия M2, обозначенного треугольником), пара рекуррентных соотношений для расчета W(p1) и W(p2) содержит общие части, соответствующие общим частям планов p1 и p2. Это дает возможность сократить вычисления для W(p2) после вычисления W(p1) (блоки 4–5 и блоки 6–9 на рис. 2).
Анализ функционирования разработанного программного комплекса решения задачи с использованием фрагментарно контролируемого случайного поиска показал, что он позволяет сократить время решения задачи не менее, чем в 3 раза, но при этом затраты оперативной памяти возрастают на 50 %.
На основе метода планирования ИД разработаны методика планирования ИД и реализующий ее программный комплекс. Его использование позволило уточнить планы ИД, разрабатываемые эвристическим путем.
По сравнению с планом ИД, полученным эвристическим путем, оптимальный план дал возмож-
 ность изменить в среднем на 15 % состав инновационных модернизационных мероприятий, на 42 % способы реализации этих мероприятий. Это позволило достичь значения 0,74 показателя успешности ИД для полученного оптимального плана, что на 14 % выше, чем значение 0,65 для эвристического плана.
ность изменить в среднем на 15 % состав инновационных модернизационных мероприятий, на 42 % способы реализации этих мероприятий. Это позволило достичь значения 0,74 показателя успешности ИД для полученного оптимального плана, что на 14 % выше, чем значение 0,65 для эвристического плана.
В результате проведенных исследований предложены постановка задачи планирования ИД как оптимизационной задачи распределения ограниченных ресурсов, а также метод фрагментарно контролируемого случайного поиска для решения оптимизационной задачи планирова- ния ИД.
Полученные результаты позволяют на практике улучшить на 10–15 % показатели успешности инновационной деятельности.
Литература
1. Седлов Е.В. Задача планирования инновационной деятельности // Отраслевые аспекты технических наук. 2011. № 8. С. 34–39.
2. Гейда А.C., Лысенко И.В., Силла Е.П. Задачи исследования качества и потенциала систем реализации целевых программ // Информационно-управляющие системы. 2011. № 4. С. 77–83.
3. Гейда А.C. Оценивание эффектов функционирования организационно-технических систем: концепция автоматизации: тр. СПИИРАН, 2009. № 11. С. 63–80.
4. Гейда А.C., Лысенко И.В., Юсупова О.А. Использование расширенных графовых моделей при автоматизации решения задач исследования потенциала, эффективности и риска при функционировании социально-экономических систем // Региональная информатика-2010: тр. XII СПб междунар. конф. СПб, 2011. С. 47–59.
5. Лысенко И. В. Оценивание качества технологических процессов: использование аппроксимирующих вероятностных моделей: тр. СПИИРАН, 2006. № 3. С. 207–216.
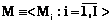 ;
;  – это Mi при pi-м способе его реализации,
– это Mi при pi-м способе его реализации, 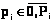 : pi=0, если
: pi=0, если 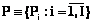 ;
; 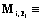
 ;
; 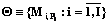 ;
; 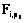 – вектор характеристик способа реализации
– вектор характеристик способа реализации 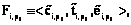 где
где 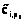 – случайная величина материальных затрат на реализацию
– случайная величина материальных затрат на реализацию 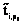 – случайная величина длительности
– случайная величина длительности  – размер множества
– размер множества 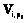 мероприятий МПД, затронутых реализацией
мероприятий МПД, затронутых реализацией 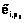 – вектор эффектов каждого мероприятия Vl МПД:
– вектор эффектов каждого мероприятия Vl МПД: 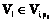 ;
;  ;
;  – вектор случайных величин эффектов l-го мероприятия МПД при выполнении
– вектор случайных величин эффектов l-го мероприятия МПД при выполнении 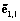 – случайная величина материальных затрат на реализацию такого мероприятия;
– случайная величина материальных затрат на реализацию такого мероприятия; 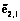 – случайная величина временных затрат на его реализацию;
– случайная величина временных затрат на его реализацию; 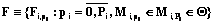 ;
; 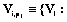
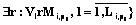 ; r – отношение зависимости между мероприятиями Vl и
; r – отношение зависимости между мероприятиями Vl и  ;
; 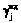 – сетевой график МПД для достижения j-й цели Gj,
– сетевой график МПД для достижения j-й цели Gj,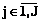 ;
; 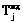 – вектор плановых моментов времени начала МПД по графику
– вектор плановых моментов времени начала МПД по графику 
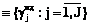 ;
; 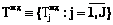 ;
; 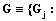
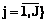 ;
;  – s-й план ИД из множества P возможных планов: psÎP;
– s-й план ИД из множества P возможных планов: psÎP; 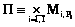 ; popt – оптимальный план ИД; W(ps) – показатель качества инновационной и производственной деятельности при плане ps;
; popt – оптимальный план ИД; W(ps) – показатель качества инновационной и производственной деятельности при плане ps; 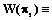

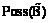 – мера возможности наступления случайного события
– мера возможности наступления случайного события  ;
; 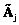 – событие, состоящее в актуализации цели Gj;
– событие, состоящее в актуализации цели Gj;  – случайный момент времени окончания МПД в соответствии с
– случайный момент времени окончания МПД в соответствии с 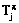 – директивный (требуемый) момент окончания МПД в соответствии с
– директивный (требуемый) момент окончания МПД в соответствии с  ;
;  – случайная сумма денежных средств, расходуемых на ИММ и МПД в соответствии с планом ps для достижения цели Gj;
– случайная сумма денежных средств, расходуемых на ИММ и МПД в соответствии с планом ps для достижения цели Gj; 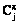 – директивная (назначенная) сумма денежных средств, выделенных на ИММ и МПД для достижения цели Gj;
– директивная (назначенная) сумма денежных средств, выделенных на ИММ и МПД для достижения цели Gj; 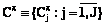 ;
; 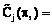
 ,
, 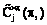 – сумма денежных средств, расходуемых на реализацию ИД в соответствии с планом ps для достижения цели Gj;
– сумма денежных средств, расходуемых на реализацию ИД в соответствии с планом ps для достижения цели Gj; 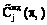 – сумма денежных средств, расходуемых на реализацию МД по графику
– сумма денежных средств, расходуемых на реализацию МД по графику  . Тогда решаемая задача примет следующий вид.
. Тогда решаемая задача примет следующий вид.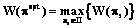 .
.

