Journal influence
Bookmark
Next issue
Constructing perfect normal forms of Boolean functions for circuit implementations of authentication protocols using Maple
Abstract:One of the promising areas of applying discrete mathematics are zero-knowledge authentication protocols based on modular residue class codes (MRCC). Using MRCC allows replacing a computing device that implements the operation of raising to a power modulo with a code converter. As a result, a complex computational operation is executable in one machine phase. It is obvious that the efficiency of code converters depends largely on the correct transition from the truth table to perfect normal forms of Boolean functions. The authors of this article have developed a software code and a graphical application for a computer that allows obtaining perfect disjunctive or conjunctive forms in accordance with the content of the truth tables described by the user and displaying the result in the corresponding field in mathematical form. Perfect forms can be obtained using the description of the truth table both in the form of minterms (maxterms) of a Boolean function using the logical variables true or false, and using the numbers of sets of minterms (maxterms). There is a possibility to choose the type of the obtained perfect form. The developed application contains reference data on its use. The software code and the entire graphical user interface are written using the built-in language of the Maple computer algebra system, as well as using the Maplet library. It was possible to create an interactive application that is user-friendly for non-professional programmers (mathematics teachers, students). For the convenience of the end user, the program is designed as a graphical application that requires only the Maple system installed. The developed application can be used by educational organizations that study the academic disciplines of mathematical logic, discrete mathematics or their sections.
Аннотация:Одной из перспективных областей применения дискретной математики являются протоколы аутентификации с нулевым разглашением знаний, построенные на основе модулярных кодов класса вычетов. Использование этих кодов позволяет заменить вычислительное устройство, реализующее операцию возведения в степень по модулю, на кодопреобразователь. В результате сложная вычислительная операция будет выполнена за один такт. Эффективность работы кодопреобразователей во многом зависит от правильности перехода от таблицы истинности к совершенным нормальным формам булевых функций. Авторами данной статьи разработаны программный код и графическое интерактивное приложение для ЭВМ, которое позволяет получать совершенные дизъюнктивные и (или) совершенные конъюнктивные нормальные формы согласно описанному пользователем содержанию таблиц истинности и выводить результат в соответствующем поле с использованием логических функций библиотеки Logic или в виде формулы. Совершенные формы можно получить с использованием описания таблицы истинности в виде минтермов (макстермов) булевой функции, а также номеров наборов минтермов (макстермов). В разработанном приложении существует возможность выбора типа получаемой совершенной формы, и оно содержит справочные данные по использованию. Программный код и весь графический интерфейс написаны с помощью встроенного языка и библиотек системы компьютерной алгебры Maple. Созданное интерактивное приложение интуитивно понятно и доступно даже непрофессиональным программистам (преподавателям математики, студентам). Для удобства программный код оформлен в виде графического приложения, требующего для работы установленной на компьютере системы Maple. Разработанное приложение может быть использовано образовательными организациями, в которых преподаются математическая логика, дискретная математика или их разделы.
| Authors: Olenev, A.A. (olenevalexandr@gmail.com) - Stavropol State Pedagogical Institute (Associate Professor of the Department of Mathematics, Informatics and Digital Educational Technologies), Stavropol, Russia, Ph.D, Kalmykov, I.A. (kia762@yandex.ru) - North Caucasian Federal University (Professor of the Department of Information Security of Automated Systems), Stavropol, Russia, Ph.D, Kirichek, K.A. (kirichekka@mail.ru) - Stavropol State Pedagogical Institute (Head of Chair of the Department of Mathematics, Informatics and Digital Educational Technologies), Stavropol, Russia, Ph.D | |
| Keywords: Maple, computer algebra systems, perfect disjunctive and conjunctive normal forms, Boolean functions, mathematical logic |
|
| Page views: 1686 |
PDF version article |
Появление низкоорбитальных систем спутникового Интернета делает достаточно актуальной проблему аутентификации космических аппаратов. Это связано с тем, что увеличение числа их группировок (например, Starlink содержит более 2 000 спутников) приводит к повышению вероятности навязывания неавторизованного контента чужим спутником. Для предотвращения такого деструктивного воздействия в работах [1, 2] предлагается использовать систему опознавания космических аппаратов, построенную на основе протокола аутентификации с нулевым разглашением знаний. В этом протоколе проверяющий (запросчик) генерирует сигнал-вопрос, который передается претенденту (ответчику). В зависимости от полученного сигнала-вопроса претендент вычисляет ответ и передает его проверяющему. Запросчик проверяет данный ответ. Если он правильный, претендент считается авторизованным абонентом. Для обеспечения высокой имитостойкости к подбору правильного ответа в этих протоколах применяются операции возведения в степень по модулю Q. Так как в качестве модуля используются большие простые числа, на выполнение операций с ними требуются значительные временные затраты. В результате увеличивается интервал, в течение которого злоумышленник может подбирать правильный ответ. Уменьшить временные затраты на опознание спутника можно за счет использования модулярных кодов классов вычетов (МККВ), являющихся арифметическими [3–5]. Для построения МККВ выбираются простые числа p1, p2, …, pn, для которых справедливо
p1 < p2 < …< pn. (1) Это основания модулярного кода. Их произведение определяет диапазон МККВ:
Тогда любое целое число A < Pn можно однозначно представить в виде набора остатков, получаемых при делении числа А на основания МККВ, A = (a1, a2, …, an), (3) где ai º Amod pi, i = 1, …, n. В МККВ модульные операции можно свести к соответствующим операциям над остатками. Пусть заданы два простых числа: A = = (a1, a2, …, an) и W = (w1, w2, …, wn). Тогда для операций сложения, вычитания и умножения справедливо
где wi º Wmod pi, i = 1, …, n. Использование модулярного кода классов вычетов позволяет повысить скорость выполнения модульных операций. Анализ выражений (4)–(6) показывает, что в МККВ вычисления выполняются параллельно по основаниям кода. Рассмотрим это на примере. Пусть заданы основания МККВ p1 = 2, p2 = 3, p3 = 5. Рабочий диапазон равен 30. Выполним операцию умножения двух чисел: A = 4 = (0, 1, 4) и W = 7= (1, 1, 2). Получаем A × W = ((0 × 1)mod2, (1 × 1)mod3, (4 × 2)mod5) = = (0, 1, 3) = 28. Разрядность операндов-остатков a1, a2, …, an значительно меньше самого числа А, что также позволяет повысить скорость вычислений. Например, если в качестве оснований МККВ взять шестиразрядные простые числа p1 = 37, p2 = 41, p3 = 43, p4 = 47, p5 = 53, p6 = 59, p7 = 61, то рабочий диапазон МККВ Pn = = 584803025179. Тогда число A = 584803025170 можно представить в виде набора остатков МККВ: A = (28, 32, 34, 38, 44, 50, 52). В этом случае 40-разрядное число представляется в виде набора шестиразрядных остатков. Очевидно, что использование МККВ позволяет повысить скорость выполнения модульных операций. Тогда, подобрав основания МККВ так, чтобы выполнилось условие Pn > Q, операцию вычисления истинного статуса спутника в протоколе аутентификации [2]
можно заменить на n параллельных вычислений в МККВ:
где U, S[j], T[j] – секретные параметры протокола на j-м сеансе аутентификации; g – порождающий элемент мультипликативной группы по модулю pi; Ui º Umod pi, S[j] º S[j]mod pi, T[j] º T[j]mod pi, i = 1, …, n. Дальнейшего снижения временных затрат на аутентификацию космического аппарата можно достичь за счет использования вместо вычислительного устройства, выполняющего операцию возведения в степень по модулю pi, кодопреобразователя. Если на его вход подать значение показателя степени, например Si[j], то на выходе получим значение Эту мультипликативную операцию можно выполнить с помощью кода преобразователя. Если на его вход подать число 5, то на вы- ходе кодопреобразователя появится число 10. В данном случае операция возведения в степень по модулю выполнится за один такт. Однако для разработки такого преобразователя необходимо грамотно использовать методы дискретной математики. Освоение разделов дискретной математики и математической логики предполагает изучение таких тем, как множества, математическая индукция, математическая логика, отношения, функции, анализ алгоритмов, теория графов, комбинаторика, теория вероятностей, рекуррентные соотношения [6–8]. Усвоение этих разделов позволяет понять и решить задачу синтеза кодопреобразователя, которая состоит в построении схемы для заданной булевой функции или системы булевых функций на основе определенной системы логических элементов. Как правило, исходное описание для синтеза схемы задается либо в виде таблицы истинности, либо в аналитической форме в виде формулы [9]. При решении задачи синтеза комбинационной схемы, реализующей заданную булеву функцию, предварительно производятся минимизация булевой функции и дальнейшее упрощение минимальной формы путем факторизации и декомпозиции [10, 11]. Комбинационная схема строится в заданном базисе [12]. Вопросы построения и оптимизации функционально-структурных описаний цифровых устройств рассмотрены в [13]. Методы, алгоритмы и программы решения задач минимизации дизъюнктивных нормальных форм (ДНФ) представлений булевых функций, которые широко используются при проектировании цифровых систем для уменьшения сложности (площади кристаллов) функциональных комбинационных блоков, рассмотрены, например, в [14, 15]. Анализ источников и задачи синтеза кодопреобразователя (комбинационной схемы) показывает необходимость построения совершенных дизъюнктивных нормальных форм (СДНФ) или совершенных конъюнктивных нормальных форм (СКНФ) по таблицам истинности, являющихся одним из наиболее наглядных элементов формальной логики и одной из возможных форм представления функционирования комбинационного аппарата. То есть необходимо получить ДНФ (КНФ), называемую канонической или совершенной, причем все ее элементарные конъюнкции (дизъюнкции) являются конституентами единицы (нуля). При этом элементарные конъюнкции (дизъюнкции) называются конституентами единицы (нуля), если содержат в прямом или инверсном виде все переменные, являющиеся аргументами булевой функции [9]. Для решения задач дискретной математики и математической логики можно использовать средства вычислительной техники: так, вопросы использования методов дискретной математики и описания важнейших алгоритмов на дискретных структурах изложены в [16–18]. Для работы с элементами логики и булевой алгебры и их изучения можно использовать систему компьютерной алгебры Maple [8, 19, 20]. Эта система универсальна, гибка в использовании, одна из немногих, имеющих свою библиотеку для работы с булевыми функциями Logic, которая позволяет наглядно представить построение таблиц истинности (соответствия) и исследовать логическую эквивалентность составных высказываний. Однако библиотека Logic не имеет встроенных функций, позволяющих описать минтерм или макстерм и, соответственно, получить СДНФ или СКНФ согласно запросу пользователя. Таким образом, несмотря на очевидную полезность и необходимость функций библио- теки Logic, система не предусматривает описания таблицы истинности, а результаты преобразований составных высказываний выдает в упрощенном виде, который не всегда совпадает с совершенными формами. В связи с этим предлагается программное решение, позволяющее развить систему Maple, а точнее – ее библиотеку Logic. Его использование в процессе обучения будет способствовать улучшению понимания обучающимися построения для булевых функций СДНФ и СКНФ, а также позволит изучать дискретную математику, математическую логику и другие дисциплины с использованием системы компьютерной алгебры. Исследования по созданию программных кодов для изучения математической логики проводят как отечественные [21, 22], так и зарубежные [23–25] специалисты. В работе [22] представлены исходные коды для изучения различных разделов дискретной математики в виде программных рабочих листов, в том числе и булевой алгебры, и исследованы основные тенденции использования системы компьютерной алгебры Maple по компьютерному экспериментированию в дискретной математике. Описаны методы доказательств законов теории множеств, получения СДНФ и СКНФ, а также предложена программная реализация этих и других методов, используемых в дискретной математике. В работе [24] представлена модификация программного исходного кода для построения СДНФ и СКНФ без упрощений. Программный код реализован на языке программирования универсальной системы компьютерной алгебры Mathematica. Это сделано, чтобы помочь студентам, изучающим дискретную математику, лучше понять процесс построения и использования булевых функций. Сегодня существуют приложения для получения СДНФ и СКНФ, написанные практически на всех популярных языках программирования, однако получение СДНФ и СКНФ по таблице истинности или в числовой форме для создания различных схемотехнических решений, в том числе и кодопребразователей, не рассматривается. В данной статье представлен способ создания исходного кода программы и интерактивного приложения для построения СДНФ и СКНФ [21, 26], полностью написанного в среде системы Maple с помощью библиотеки Maplet. Разработанное в Maple приложение для персонального компьютера может помочь полу- чить СДНФ и СКНФ по таблице истинности двумя способами: – с помощью первоначального описания макстермов или минтермов в виде набора логических констант true или false; – используя десятичные номера макстермов или минтермов (в числовой форме). Таким образом, цифровизация всех сфер жизни, в частности, образования, обусловливает актуальность создания исходного кода программы и интерактивных приложений с простым и понятным интерфейсом для выполнения разнообразных задач. Разработка процедур нахождения СДНФ и СКНФ Для получения СДНФ или СКНФ в системе Maple были созданы функции для описания минтерма или макстерма в выбранной форме, входящих в СДНФ или СКНФ соответственно, а затем выполнены дизъюнкция или конъюнкция описанных макстермов или минтермов соответственно. Рассмотрим порядок нахождения СДНФ. 1. Описание макстерма или минтерма с использованием констант true или false. Процедура Описание_таблицы_истинности_SDNF позволяет выполнять нахождение СДНФ по предъявленному условию – описание минтермов с использованием констант true или false. Данная процедура состоит из двух частей: непосредственно нахождения минтерма и объединения полученных макстермов. Аргументами для процедуры нахождения минтерма являются описание строки таблицы истинности (представленной с использованием констант true или false), принимающей значение true, и наименования используемых переменных. Чтобы создать minterm, связанный с элементом таблицы истинности, сначала инициализируется minterm, равный NULL. Затем в цикле for с переменной цикла i и диапазоном для всех используемых переменных проверяется, принимает ли описываемая переменная истинностное значение true или false. Если переменная имеет значение true, то minterm обновляется, объединяясь с именем соответствующей переменной. Если запись имеет значение false, то minterm обновляется, формируя конъюнкцию с отрицанием переменной. Итогом работы цикла является соответствующий minterm: Описание_минтерма:=proc(row:: ::list(truefalse),пер::list(symbol))% получение минтерма local минтерм, i; % используемые переменные uses Logic; if nops(row) <> nops(пер) then error "Проверьте правильность указания количества переменных"; end if; минтерм := NULL; % получение описанного минтерма for i from 1 to nops(row) do if row[i] then минтерм:= минтерм &and пер[i]; else минтерм:= минтерм &and ¬ (пер[i]); end if; end do; return минтерм; end proc:
Для завершения разработки СДНФ необходимо сформировать дизъюнкцию minterm, созданную процедурой Описание_минтерма. Вторая часть процедуры – Описание_таблицы_истинности_SDNF – использует в качестве аргументов описание строк таблицы истинности, принимающих значения true и описанных с использованием констант true или false, и наименования используемых переменных. Сначала проверяется, не был ли переданный набор пустым. Если да, то возвращается выражение false. Если аргументы заданы правильно, то инициализируется результат NULL. Для каждого необходимого элемента таблицы истинности вызывается процедура Описание_минтерма и с помощью оператора &or (операция «или») выходные данные этой процедуры добавляются к имеющемуся результату:
> Описание_таблицы_истинности_SDNF:= proc(T::set(list(truefalse)),переменные::list(symbol)) local Накопление, значения, форма; % используемые переменные if T = {} then % проверка наличия описания функции return false; end if; Накопление:= NULL; % формирование СДНФ for значения in T do форма:= Описание_минтерма(значения,переменные); Накопление:= Накопление &or форма; end do; return Накопление; end proc:
Разработанная процедура нахождения СКНФ отличается только порядком нахождения макстерма (используется операция дизъ- юнкции в системе Maple – &or) и операцией накопления результатов макстермов, то есть необходимо произвести замену операции дизъюнкции (в системе Maple – &or) на операцию конъюнкции (в системе Maple – &and). 2. Описание макстерма или минтерма в форме номера набора. Для нахождения СКНФ или СДНФ по номерам наборов дополнительно используется перевод в вид описания минтермов или макстермов с использованием констант true или false, рассмотренный ранее. Приведем фрагмент программного кода, отвечающего за данный перевод: > число:= ListTools:-Reverse(convert(x,base,2)); m:= nops(число); % определение необходимого числа разрядов в минтерме (макстерме) k:= nops(пер); % определение числа используемых переменных if m > k then error "Требуется %d цифр", m end if; % определение необходимого числа разрядов A:=[0 $ (k-m), op(число)]; % заполнение значением «нуль» избыточных разрядов for j to nops(A) do % представление числа с использованием констант true, false if A[j]=1 then A:=subsop (j=true,A) else A:=subsop(j=false,A); end if; end do: Данная процедура обеспечивает следующие преобразования: – перевод десятичного числа (номера набора) в двоичный вид; – проверка соответствия необходимого числа разрядов (строк в таблице истинности) и количества разрядов полученного числа; в случае несоответствия (меньшего числа разрядов при представлении числа в двоичном виде) заполнение недостающих позиций значениями «нуль»; – представление двоичного числа с применением констант true или false, используя цикл for. Таким образом, процедура, приведенная выше, позволяет преобразовать десятичное число в описание двоичного числа, представленного с использованием констант true или false. Полученные значения могут применяться в качестве первого аргумента процедуры Описание_таблицы_истинности_SDNF, а значит, можно получить и СДНФ, порядок получения которой описан выше. Среда разработки Современные компьютерные технологии, в том числе и система Maple, позволяют решать разнообразные задачи как дискретной математики, так и математической логики. В большинстве случаев демонстрацию решения конкретной задачи можно упростить, используя windows-приложения оконной, а не консольной категории. Система Maple позволяет создавать такие оконные приложения, поскольку имеет широкий спектр компонентов, направленных на создание графического интерфейса, обладающего функциональными возможностями, аналогичными системам визуального программирования. Эти возможности обеспечиваются использованием библиотеки Maplet. Встроенный высокоуровневый язык математических расчетов Maple дает возможность применять встроенные решения для создания новых приложений. Задачей авторов данного исследования являлось написание интерактивного приложения, полностью созданного в рамках этой программной среды, с графическим интерфейсом, выдающим СДНФ или СКНФ по выбору пользователя при вводе данных, описывающих таблицу истинности (соответствия).
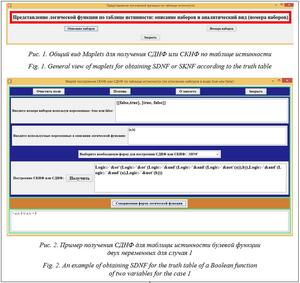
В таблице 1 показан пример ввода данных. Таблица 1 Таблица истинности Table 1 A truth table
Значения для ввода формируются следующим образом. Для первого случая (получение СДНФ с использованием описания минтерма в виде логи- ческих переменных true, false) используемые переменные a и b представляются в виде логических констант: первый набор – [false, true], второй набор – [true, false]. Итог выполнения программного кода представлен на рисунке 2.
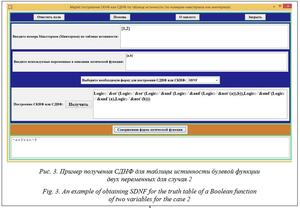
Итоговые значения совпадают, что подтверждает правильность разработанных функций. Получение СКНФ осуществляется аналогичным способом. Опишем подробнее применяемые команды для выбора необходимого представления. Нажатием кнопки «Описание наборов» открывается Maplet «Maplet построения СКНФ или СДНФ по таблице истинности (по описанию наборов в виде true или false)». Начало работы данного Maplets сопровождается вводом данных, который обеспечивает выполнение разработанной функции «Описание таблицы_истинности_SKNF_или_SDNF». Входными данными являются (T::set(list(true false)),переменные::list(symbol),вид::symbol), где переменная «Т» обеспечивает просмотр представления вводимых данных в виде описания значений таблицы истинности, принимающей значения в виде логических значений true или false, то есть используются правила описания дизъюнктивной или конъюнктивной формы. Данные переменные описывают выходные значения логической функции. Вторая составляющая, от которой зависит функция, «переменные» – обеспечивает формирование наименований переменных, от которых зависит СДНФ или СКНФ, эти данные вводятся в виде списка. Третья переменная – «вид» – указывает формируемый вид булевой функции (СДНФ или СКНФ). Нажатие функциональных кнопок «Очистить поля» и «Закрыть» приводит к выполнению описанного действия – закрытию Maplet или удалению введенных значений. Использование вспомогательных кнопок «Помощь» и «О маплете» предоставляет вспомогательную информацию о порядке использования Maplet или его предназначении. Выпадающий список позволяет подключить необходимый порядок вычисления (обеспечивает подключение необходимых функций вычисления). Приведем фрагмент програм- много кода, осуществляющего такой вывод: > Описание_таблицы_истинности_ SKNF_или_SDNF_по_номерам := proc(T::set (nonnegint),переменные::list(symbol), вид::symbol) local Накопление, значения, форма; % используемые переменные if вид=SDNF then СДНФ_по_но- мерам(T,переменные); % процедуры для преобразования elif вид=SKNF then СКНФ_по_но- мерам(T,переменные); else error "Нет такой формы"; end if; end proc: Создание графического интерфейса пользователя для программного кода Для разработки интерактивного приложения получения СДНФ или СКНФ в зависимости от вводимых данных использован метод визуально-ориентированного программирования [19]. Данный метод представлен в Maple с использованием специальной библиотеки Maplet, функции которой обеспечивают формирование графического интерфейса. Графи-ческий интерфейс разрабатываемого интерак- тивного приложения создается путем описания нужных элементов будущего приложения из этой библиотеки. Необходимые действия прописываются при активации элементов и при обработке событий элементов пользовательского интерфейса. Для удобства использования подготовленного приложения был разработан графический интерфейс GUI [27]. Нажатием кнопок «Описание наборов» и «Номера наборов» обеспечивается выбор формы вводимых данных и описания макстермов или минтермов в выбранном виде. Нажатие любой из них приводит к открытию соответствующего Maplet. При описании наборов в виде переменных true или false Maplet (Maplet построения СКНФ или СДНФ по таблице истинности (по описанию наборов в виде: true или false)) имеет три зоны действия: вспомогательную, ввода информации и вывода результата. Вспомогательная зона содержит четыре кнопки: справочные «Помощь» и «О маплете» и функциональные «Очистить поля» и «Закрыть». Зона ввода включает в себя два поля ввода информации и поле с выпадающим списком. Поля ввода обеспечивают входными данными разработанные внутренние функции Описание_таблицы_истинности_SDNF, Описание_таблицы_истинности_SKNF, СДНФ_по _номерам, СКНФ_по_номерам, то есть позволяют формировать макстерм или минтерм. Выбранное значение из поля со списком дает возможность получить булеву функцию – СДНФ или СКНФ. Зона вывода результата включает две кнопки – «Получить» и «Совершенная форма логической функции». Нажатие кнопки «Получить» позволяет сформировать СКНФ или СДНФ в соответствующем поле вывода в виде значений библиотеки Logic, а нажатие кнопки «Совершенная форма логической функции» – получить СДНФ или СКНФ в виде математической записи. Все элементы созданного интерфейса GUI для удобства использования имеют соответствующие обозначения. Виды Maplet (Maplet построения СКНФ или СДНФ по таблице истинности (по номе- рам макстермов или минтермов)) существенных отличий по структуре между собой не имеют. Выбор необходимого вида преобразования обеспечивается первоначальным выбором, а также данными, выводимыми по умолчанию. Для этого в Maplet (Maplet построения СКНФ или СДНФ по таблице истинности (по описанию наборов в виде: true или false)) по умолчанию в полях ввода выводится форма представления вводимых данных: {[true, false]}, для Maplet построения СКНФ или СДНФ по таблице истинности (по номерам макстермов или минтермов): {0}. В поле ввода «Введите используемые переменные в описание логической функции» по умолчанию выводится [a, b], то есть булева функция зависит от двух переменных. При ошибках формата ввода будет выведено сообщение об ошибке. Изменения возможны без перезапуска приложения. Существуют ограничения использования приложения: для описания входных переменных необходимо использовать строчные буквы латинского алфавита, ввод наименований с верхними или нижними индексами запрещен. Эффективность использования програм- много кода и созданного интерактивного графического приложения проверялась в ходе учебных занятий по математической логике, дискретной математике, а также в научных исследованиях при выполнении построения кодопреобразователей. Таблица 2 Усвоение учебного материала (%) Table 2 Acquisition of learning material (%)
Анализ полученных данных (табл. 2) показывает, что по сравнению с традиционными методами обучения использование как программного кода, так и интерактивного графического приложения дает улучшение понимания учебного материала от 4 до 18 процентов. Заключение Сферы применения дискретной математики постоянно расширяются. Ее методы нашли приложение в системах тестирования программных продуктов, при разработке реляционных БД, в логистике. Новой областью использования дискретной математики могут стать криптографические протоколы аутентификации, реализованные в модулярных кодах классов вычетов. С помощью данных методов можно заменить вычислительное устройство, реализующее операцию возведения в степень по модулю, на кодопреобразователь. В результате сложная вычислительная операция будет выполнена за один такт. Очевидно, что эффективность работы кодопреобразователей определяется прежде всего правильным переходом от таблицы истинности к СДНФ и СКНФ. Авторы данного исследования разработали про- граммный код и интерактивное графическое приложение для получения СДНФ и СКНФ, получаемых из описания таблицы истинности двумя способами: описанием макстермов (минтермов) с использованием логических констант true и false и описанием макстермов (минтермов) по номерам наборов. Интерактивные приложения позволяют получать представление и в виде формулы. Для написания исходного кода программ использован встроенный язык системы компьютерной алгебры Maple. Для удобства применения программные коды представлены в виде интерактивных приложений, способных к запуску на любом компьютере с установленной системой Maple. Благодаря возможности выбора вида формы данный программный код и графические интерактивные приложения можно использовать для решения широкого круга задач, связанных с синтезом простейших цифровых устройств, а также для преподавания математической логики и дискретной математики. Список литературы 1. Kalmykov I., Lapina M., Provornov I., Voloshin E. Development of imitation-resistant authentication protocol for low-orbital space satellite communication system. Ceur WS Proc., 2019, vol. 2500, pp. 1–10. 2. Pashintsev V.P., Zhuk A.P., Kalmykov M.I., Olenev A.A. Redundant modular codes for development of fault-tolerant systems of satellite identification. IJETER, 2020, vol. 8, no. 7, pp. 3160–3168. doi: 10.30534/ijeter/2020/47872020. 3. Valueva M.V., Nagornov N.N., Lyakhov P.A., Valuev G.V., Chervyakov N.I. Application of the residue number system to reduce hardware costs of the convolutional neural network implementation. Math. and Comput. in Simulation, 2020, vol. 177, рр. 232–243. doi: 10.1016/j.matcom.2020.04.031. 4. Tchernykh A., Schwiegelsohn U., Talbi E., Babenko M. Towards understanding uncertainty in cloud computing with risks of confidentiality, integrity, and availability. J. of Computational Sci., 2019, vol. 36, art. 100581. doi: 10.1016/j.jocs.2016.11.011. 5. Samimi N., Kamal M., Afzalli-Kusha A., Pedram M. Res-DNN: A Residue number system-based DNN accelerator unit. IEEE Transactions on Circuits and Systems I: Regular Papers, 2020, vol. 67, no. 2, рр. 658–671. doi: 10.1109/TCSI.2019.2951083. 6. Mosley A. An Introduction to Logic: From Everyday Life to Formal Systems. Northampton, Massachusetts, 2019, 385 p. 7. O’Leary M.L. A First Course in Mathematical Logic and Set Theory. NJ, John Wiley & Sons Publ., 2016, 416 p. 8. Rosen K.H. Discrete Mathematics and its Applications. NY, McGraw-Hill Publ., 2019, 1118 p. 9. Rusnak P. Transformation of Boolean expression into disjunctive or conjunctive normal form. CERes J., 2017, vol. 3, no. 1, pp. 43–49. 10. Бибило П.Н., Романов В.И. Система логической оптимизации функционально-структурных описаний цифровых устройств на основе продукционно-фреймовой модели представления знаний // Проблемы разработки перспективных микро- и наноэлектронных систем. 2020. № 4. С. 9–16. doi: 10.31114/2078-7707-2020-4-9-16. 11. Михеева Е.А., Еникеева А.Ф. Минимизация булевых функций геометрическим методом // Ученые записки УлГУ. Сер. Математика и информационные технологии. 2018. № 1. С. 72–82. 12. Riznyk V., Solomko M. Minimization of Boolean functions by combinatorial method. Technology Audit and Production Reserves, 2017, vol. 4, no. 36, pp. 49–64. doi: 10.15587/2312-8372.2017.108532. 13. Feng J., Zhao R., Cui Y. Simplification of logical functions with application to circuits. Electronic Research Archive, 2022, vol. 30, no. 9, pp. 3320–3336. doi: 10.3934/era.2022168. 14. Поттосин Ю.В. Метод многоблочной параллельной декомпозиции системы частичных булевых функций // Информатика. 2017. № 3. С. 92–98. 15. Поттосин Ю.В. Параллельная декомпозиция системы частичных булевых функций // Вестн. ТГУ. УВТиИ. 2018. № 45. С. 83–91. doi: 10.17223/19988605/45/10. 16. Alharbi E. Truth graph: A novel method for minimizing Boolean algebra expressions by using graphs. In: LNAI. Proc. Diagrams, 2020, pp. 461–469. doi: 10.1007/978-3-030-54249-8_36. 17. Martin É. Disjunctive logic programs, answer sets, and the cut rule. Archive for Math. Logic, 2022, vol. 61, no. 7-8, pp. 903–937. doi: 10.1007/s00153-022-00821-x. 18. Rozo J.H.B. Using Boolean algebra to model the economic decision-making. Brazilian J. of Business, 2021, vol. 3, no. 2, pp. 1413–1426. doi: 10.34140/bjbv3n2-009. 19. Оленев А.А., Киричек К.А., Потехина Е.В. Математическая логика: построение логических схем из логических элементов в Maple // Вестн. КРАУНЦ. Физико-матем. науки. 2021. Т. 36. № 3. С. 155–164. doi: 10.26117/2079-6641-2021-36-3-155-164. 20. Durcheva M., Varbanova E. Applications of CAS in the teaching and learning of discrete mathematics. Math. in Comput. Sci., 2017, vol. 11, pp. 305–314. doi: 10.1007/s11786-017-0310-8. 21. Olenev A.A., Zvereva L.G., Saieg T.H. Improving the learning and teaching of mathematical logic elements using Maple. JHETP, 2022, vol. 22, no. 8, pp. 51–57. doi: 10.33423/jhetp.v22i8.5315. 22. Оленев А.А., Киричек К.А., Потехина Е.В. Программа для визуализации основных логических операций: Свид. о регистр. ПрЭВМ № 2021613965. Рос. Федерация, 2021. 23. Durcheva M., Nikolova E. Modeling mathematical logic using MAPLE. AIP Conf. Proc., 2018, vol. 2048, art. 060010. doi: 10.1063/1.5082125. 24. Nieto S., Ramos H. Constructing extended Boolean functions from truth tables using the Mathematica system. Proc. SIIE, 2016, pp. 1–6. doi: 10.1109/SIIE.2016.7751828. 25. Бибило П.Н., Логинова И.П. Экспериментальное сравнение эффективности программ минимизации систем булевых функций в классе дизъюнктивных нормальных форм // Информатика. 2022. Т. 19. № 2. С. 26–55. 26. Оленев А.А., Калмыков И.А., Киричек К.А., Проворнов И.А. Программа для визуализации построения совершенных нормальных форм формул алгебры логики: Свид. о регистр. ПрЭВМ № 2023614273. Рос. Федерация, 2023. 27. Thompson I. Understanding Maple. UK, Cambridge University Press, 2017, 233 p. Reference List 1. Kalmykov, I., Lapina, M., Provornov, I., Voloshin, E. (2019) ‘Development of imitation-resistant authentication protocol for low-orbital space satellite communication system’, Ceur WS Proc., vol. 2500, pp. 1–10. 2. Pashintsev, V.P., Zhuk, A.P., Kalmykov, M.I., Olenev, A.A. (2020) ‘Redundant modular codes for development of fault-tolerant systems of satellite identification’, IJETER, 8(7), pp. 3160–3168. doi: 10.30534/ijeter/2020/47872020. 3. Valueva, M.V., Nagornov, N.N., Lyakhov, P.A., Valuev, G.V., Chervyakov, N.I. (2020) ‘Application of the residue number system to reduce hardware costs of the convolutional neural network implementation’, Math. and Comput. in Simulation, 177, рр. 232–243. doi: 10.1016/j.matcom.2020.04.031. 4. Tchernykh, A., Schwiegelsohn, U., Talbi, E., Babenko, M. (2019) ‘Towards understanding uncertainty in cloud computing with risks of confidentiality, integrity, and availability’, J. of Computational Sci., 36, art. 100581. doi: 10.1016/j.jocs.2016.11.011. 5. Samimi, N., Kamal, M., Afzalli-Kusha, A., Pedram, M. (2020) ‘Res-DNN: A Residue number system-based DNN accelerator unit’, IEEE Transactions on Circuits and Systems I: Regular Papers, 67(2), рр. 658–671. doi: 10.1109/TCSI.2019.2951083. 6. Mosley, A. (2019) An Introduction to Logic: From Everyday Life to Formal Systems. Northampton, Massachusetts, 385 p. 7. O’Leary, M.L. (2016) A First Course in Mathematical Logic and Set Theory. NJ: John Wiley & Sons Publ., 416 p. 8. Rosen, K.H. (2019) Discrete Mathematics and its Applications. NY: McGraw-Hill Publ., 1118 p. 9. Rusnak, P. (2017) ‘Transformation of Boolean expression into disjunctive or conjunctive normal form’, CERes J., 3(1), pp. 43–49. 10. Bibilo, P.N., Romanov, V.I. (2020) ‘The system of logical optimization of functional structural descriptions of digital circuits based on production-frame knowledge representation model’, Problems of Advanced Micro- and Nanoelectronic Systems Development, (4), pp. 9–16 (in Russ.). doi: 10.31114/2078-7707-2020-4-9-16. 11. Mikheeva, E.A., Enikeeva, A.F. (2018) ‘Minimization of Boolean functions by a geometric method’, Scientific Notes of UlGU. Series: Mathematics and Information Technology, (1), pp. 72–82 (in Russ.). 12. Riznyk, V., Solomko, M. (2017) ‘Minimization of Boolean functions by combinatorial method’, Technology Audit and Production Reserves, 4(36), pp. 49–64. doi: 10.15587/2312-8372.2017.108532. 13. Feng, J., Zhao, R., Cui, Y. (2022) ‘Simplification of logical functions with application to circuits’, Electronic Research Archive, 30(9), pp. 3320–3336. doi: 10.3934/era.2022168. 14. Pottosin, Yu.V. (2017) ‘A method for multi-block parallel decomposition of a system of partial Boolean functions’, Informatics, (3), pp. 92–98 (in Russ.). 15. Pottosin, Yu.V. (2018) ‘Parallel decomposition of a system of partial Boolean functions’, Tomsk State University J. of Control and Comput. Sci., (45), pp. 83–91 (in Russ.). doi: 10.17223/19988605/45/10. 16. Alharbi, E. (2020) ‘Truth graph: A novel method for minimizing Boolean algebra expressions by using graphs’, in LNAI. Proc. Diagrams, pp. 461–469. doi: 10.1007/978-3-030-54249-8_36. 17. Martin, É. (2022) ‘Disjunctive logic programs, answer sets, and the cut rule’, Archive for Math. Logic, 61(7-8), pp. 903–937. doi: 10.1007/s00153-022-00821-x. 18. Rozo, J.H.B. (2021) ‘Using Boolean algebra to model the economic decision-making’, Brazilian J. of Business, 3(2), pp. 1413–1426. doi: 10.34140/bjbv3n2-009. 19. Olenev, A.A., Kirichek, K.A., Potekhina, E.V. (2021) ‘Mathematical logic: Construction of logic circuits from logical elements in Maple’, Bull. KRASEC. Physical and Math. Sci., 36(3), pp. 155–164 (in Russ.). doi: 10.26117/2079-6641-2021-36-3-155-164. 20. Durcheva, M., Varbanova, E. (2017) ‘Applications of CAS in the teaching and learning of discrete mathematics’, Math. in Comput. Sci., 11, pp. 305–314. doi: 10.1007/s11786-017-0310-8. 21. Olenev, A.A., Zvereva, L.G., Saieg, T.H. (2022) ‘Improving the learning and teaching of mathematical logic elements using Maple’, JHETP, 22(8), pp. 51–57. doi: 10.33423/jhetp.v22i8.5315. 22. Olenev, A.A., Kirichek, K.A., Potekhina, E.V. (2021) Program for Visualization of basic Logical Operations, Pat. RF, № 2021613965. 23. Durcheva, M., Nikolova, E. (2018) ‘Modeling mathematical logic using MAPLE’, AIP Conf. Proc., 2048, art. 060010. doi: 10.1063/1.5082125. 24. Nieto, S., Ramos, H. (2016) ‘Constructing extended Boolean functions from truth tables using the Mathematica system’, Proc. SIIE, pp. 1–6. doi: 10.1109/SIIE.2016.7751828. 25. Bibilo, P.N., Loginova, I.P. (2022) ‘Experimental comparison of the effectiveness of programs for minimizing systems of Boolean functions in the class of disjunctive normal forms’, Informatics, 19(2), pp. 26–55 (in Russ.). doi: 10.37661/1816-0301-2022-19-2-26-55. 26. Olenev, А.A., Kalmykov, I.A., Kirichek, K.A., Provornov, I.A. (2023) A Program for Visualizing the Construction of Perfect Normal Forms of Logic Algebra Formulas. Pat. RF, № 2023614273. 27. Thompson, I. (2017) Understanding Maple. UK: Cambridge University Press, 233 p. |
| Permanent link: http://swsys.ru/index.php?page=article&id=5010&lang=&lang=en&like=1 |
Print version |
| The article was published in issue no. № 3, 2023 [ pp. 349-360 ] |
Perhaps, you might be interested in the following articles of similar topics:
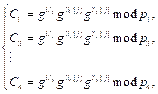 (8)
(8)