Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (koganow@niisi.msk.ru) - , Ph.D, (sazonov@rg.ru) - | |
| Keywords: reliability, computational environment, graph, fail-safety |
|
| Page views: 14038 |
Print version Full issue in PDF (8.40Mb) |
Вычислительной средой (или итерационной сетью) называется совокупность функциональных элементов, описываемых формальными автоматами и расположенных в вершинах графа (в общем случае ориентированного), причем входная информация каждого элемента формируется как совокупность выходов элементов, расположенных в вершинах, из которых на вершину данного элемента идет стрелка графа. Такие математические конструкции широко используются для моделирования распределенных процессов на дискретных пространствах или приближенного описания процессов с непрерывным носителем. Наиболее распространены вычислительные среды для расчета схем конечных разностей и конечных элементов. В последнее время появилось много итерационно-сетевых имитационных моделей в биологии и экономике. Однако непосредственное применение модели этого типа находят в комплексах вычислительных машин, связанных в информационную сеть.
Авторы ранее исследовали отказоустойчивость вычислительных сетей на графе в модели отказа для случаев стационарного или растущего графа сети [1–4]. При этом было обнаружено свойство появления положительной вероятности неограниченно долгой безотказной работы сети при достаточно быстром наращивании. Вычислительные среды с разрушением и восстановлением Обобщенная модель вычислительной среды рассматривается в виде направленного графа с помеченными вершинами, где метки (цвета) вершин соответствуют типам узлов, а дуги – односторонним каналам передачи данных. Каждая из задач, выполняющихся на вычислительной среде, может занимать один или несколько узлов. Поэтому можно рассматривать модель задачи (МЗ), основанную на модели вычислительной сети (МВС). Такая МЗ также будет направленным графом с мечеными вершинами. Для выполнения задачи на данной вычислительной сети (ВС) необходимо, чтобы МЗ была изоморфна какому-либо подграфу МВС. Оставшаяся работоспособной часть системы в случае выхода из строя некоторых компонентов ВС называется разрушенной ВС (РВС). Поскольку задача может использовать не все узлы исходной ВС, а также из-за возможности дублирования элементов в некоторых случаях исходная задача сможет выполняться и на РВС. Для выполнения задачи на ВС необходимо ассоциировать каждую вершину МЗ с вершиной МВС того же типа, чтобы при этом в полученном образе задачи на графе МВС существовали все дуги, соответствующие дугам на графе МЗ. В данной работе рассматривается случай, когда несколько однотипных вершин графа МЗ могут быть ассоциированы с одной и той же вершиной МВС того же типа. При этом предполагается, что локальные пересылки данных с одного узла ВС на самого себя всегда возможны. Под разложимостью графа МЗ на граф МВС или РВС понимается возможность указанного отображения (гомеоморфного вложения) вершин МЗ на вершины МВС (РВС). Для исследования отказоустойчивости МЗ может быть выбрана так, чтобы ее граф совпадал с графом исходной ВС. Такая МЗ называется полной (ПМЗ). В этом случае работа задачи на РВС (при условии, что граф РВС не совпадает с графом ВС) будет возможна, если в ВС было дублирование узлов и существуют все необходимые задаче дуги графа РВС. Если на РВС выполнима модель ПМЗ, то и модель любой задачи, разрешимой на исходной МВС, разрешима на этой РВС. Модель разрушения и восстановления МВС на каждом шаге следующая. Такт работы ВС состоит из трех последовательных подтактов. В первом подтакте на множестве исправных элементов реализуется испытание Бернулли с вероятностью разрушения p. Вероятности разрушения элементов в совокупности независимы. Во втором подтакте на множестве всех разрушенных элементов (включая оставшиеся с предыдущих тактов) реализуется испытание Бернулли с вероятностью восстановления q. Вероятности восстановления элементов в совокупности независимы. В третьем подтакте проверяется разрешимость задачи на полученной РВС. Наработкой на отказ в реализации считается номер первого такта, на котором задача неразрешима. Средней наработкой T (или наработкой сети) называется математическое ожидание наработки на отказ для ПМЗ. В общем случае вычисление или оценка наработки ВС требует длительного численного эксперимента. Для простейших графов иногда удается провести аналитический расчет [5]. Изменяемая вычислительная сеть (ИВС) – сеть, у которой на каждом такте изменяется граф связи элементов. При этом новый граф включает предыдущий, то есть сеть растет. Это соответствует введению нулевого подтакта, на котором вводятся несколько новых вершин и дуг графа сети. Каждой новой вершине сопоставлен некий тип элемента, который первоначально находится в рабочем состоянии. Однако уже на первом подтакте он может разрушиться. Соответственно, совокупность текущих состояний элементов вершин графа (рабочее/разрушен) на каждом такте после второго подтакта (частичное восстановление) назовем разрушенной ИВС (РИВС). Растущие корпоративные ВС Теоретически важным частным случаем, дающим аппарат для анализа ИВС общего вида, является ВС с полным графом связи между элементами одного типа (МВС в этом случае – полный немеченый граф). Такие сети входят в класс корпоративных сетей (МВС – полный меченый граф) [3]. Определение 1. Такт работы корпоративной сети определяется как два испытания Бернулли на элементах сети: процесс разрушения (D) и процесс восстановления (R). Процесс D происходит только на элементах в макросостоянии 1. Он с вероятностью p меняет их макросостояние на 0 (разрушен). Процесс R происходит только на элементах в макросостоянии 0. Он с вероятностью q переводит их в макросостояние 1 (исправен). Имеются два режима работы сети в зависимости от последовательности процессов D и R на каждом такте: с ремонтом перед выполнением задания (последовательность DR) и после выполнения задания (последовательность RD). Теорема 1. Обозначим
то имеется положительная вероятность H безотказной работы корпоративной сети неограниченное время. Если хотя бы для одного типа элементов выполнено условие
то с вероятностью 1 отказ сети наступит за конечное число тактов. Теорема 2. Если принять параметрический закон роста
то критическая точка параметра Фазовый переход отказоустойчивости корпоративной сети по скорости роста имеет вид: Приведем доказательство теорем. Аналитическая оценка вероятности отказа растущей корпоративной ВС. Рассмотрим растущую корпоративную сеть, в которой задано число элементов сети типа i на такте работы t: Тогда
Далее будем исходить из условий вероятности разрушения и восстановления, обеспечивающих антимонотонную зависимость вероятности отказа от числа исправных элементов на предыдущем такте. Это достаточно малая вероятность восстановления. Лемма 1. При Доказательство. Рассмотрим режим RD. Тогда, если k – число элементов, которые были восстановлены до начала нового разрушения, то
Первый член этого выражения соответствует значению k, которое есть при значении параметра n, но отсутствует при n+1. Разность под знаком суммы соответствует k, общему для обоих значений параметра. Неравенство следует из условия теоремы p/(1-q)<1. Это доказывает антимонотонность функции u(n). Рассмотрим режим DR. Для этого случая восстановление происходит после разрушения. Поэтому Эта функция всегда антимонотонна. При выполнении условий леммы 1 верна оценка для любого
Для режима с ремонтом после выполнения задания Для режима с ремонтом перед выполнением задания С учетом условия
Верна оценка для любого
Тогда из (6a) и (6b)
Поскольку разрушения и восстановления элементов разных типов происходят независимо, вероятность безотказной работы системы
Лемма 2. Если выполнено условие антимонотонности (лемма 1), то вероятность сохранения заданное время каждого типа элементов сети заключена между двумя геометрическими прогрессиями (6) и (7), зависящими от режима работы сети. В режиме DR обе оценки выше. Для вероятности отказа сети в зависимости от режима верны оценки (8) или (9), также геометрические прогрессии. Фазовый переход в растущей сети. Исследуем, при каком темпе роста числа элементов каждого типа возникает положительная вероятность безотказной работы сети неограниченное время. Используем нижние оценки (5) и (6). Обозначим
Из (5) следует
Определим Из (10) следует
Рассмотрим ситуацию, когда
Используем (10a) для режима DR:
Неравенство (11) в силу (12) эквивалентно условию Это и есть условие на скорость роста Тогда условие (13) соответствует Аналогично используем верхнюю оценку (7):
Из (10b) следует:
Поэтому условие (14) соответствует
Для степенной шкалы скорости роста
Теорема 1 следует из (13) и (15). Теорема 2 следует из (16) и (17), поскольку расходимость рядов (17) соответствует условию Замечание 1. Условия (1) и (2) выделяют некий диапазон последовательностей Замечание 2. Внутри указанного в теореме 2 интервала значений критической точки (3) использованный метод анализа не дает информацию о поведении вероятности отказа. Замечание 3. Выбор степенной шкалы роста произвольный. В каждом параметрическом классе функций условие (1) будет соответствовать специфичной критической точке и особой зависимости числа элементов сети от времени. Сами условия (1) и (2) непараметрические. В этом смысле можно говорить о непараметрическом фазовом переходе по скорости роста сети. Алгоритмы роста ИВС Теоремы 1 и 2 позволяют утверждать, что получить положительную вероятность неограниченного времени работы сети можно, добавив к исходной сети растущую корпоративную сеть с подходящим составом типов элементов. Действительно, если число вершин каждого типа в полном графе не меньше, чем в графе исходной сети, то ее можно изоморфно вложить в полный граф. Это означает, что доказанный фазовый переход имеет место и в случае произвольной исходной сети при некотором алгоритме ее роста. Однако указанный алгоритм предполагает возможность объединения элементов сети в полный граф, что не всегда выполняется для реального оборудования вычислительных сетей. Например, непонятно, как объединить в полный граф процессор, монитор и принтер. Поэтому требуется найти алгоритм изменения ВС, не предполагающий введения связей между элементами таких типов, которые не связаны в исходной сети. ИВС моделируются алгоритмом нулевого подтакта. Рассмотрим три алгоритма, которые применимы к любой начальной ВС и не вводят связей между элементами двух разных типов, если их не было в исходной сети. Последнее требование с прикладной точки зрения соответствует учету технологических ограничений, которые действуют для данной ВС. При этом полная задача соответствует исходной сети. Алгоритм 1. Простое дублирование сети. На нулевом подтакте добавляется Для такой сети отказа нет, если хотя бы одна компонента не дает отказа. В теории надежности это соответствует горячему резерву. Вероятность отказа
Алгоритм 2. Связное дублирование сети. На нулевом подтакте добавляется n(t) новых экземпляров (копий) исходной сети. Затем на элементах всех экземпляров, которые соответствуют одному элементу исходного графа, строится полный граф, а на объединении вершин всех экземпляров исходной ВС строятся дуги, соединяющие те пары элементов (с учетом ориентации), у которых соединены дугой прообразы в исходном графе. Новый граф соответствует дублированию каждой вершины исходного графа с кратностью m(t). Такая сеть соответствует снижению вероятности отказа элемента исходной сети: При этом вероятность восстановления Алгоритм 3. Селективное дублирование элементов. Строится полный граф на элементах простого дублирования сети, а потом убираются все дуги между парами элементов тех типов, которые не имеют связи в исходном графе сети. Алгоритмы 1 и 2 дают подграфы (иногда собственные) этого графа. Теорема 3. Если исходная ВС содержит хотя бы одну дугу, соединяющую элементы разных типов, то наработка при простом дублировании ниже, чем при связном дублировании той же кратности m(t). Доказательство. Представим случайный процесс отказов и восстановлений элементов сетей двух указанных видов как параметрические функции с параметром времени t (число тактов работы всех сетей) на пространстве случайных событий с вероятностной мерой Значением каждой такой функции будет конфигурация отказов на элементах соответствующей сети на указанном такте. Для наших целей удобно определить функции, соответствующие разным сетям как коррелированные, но без корреляции отказов элементов для каждой сети. Соответственно, сети обозначим А, В. Исходную сеть обозначим С (дублирование состоит из экземпляров С* этой сети). Назовем элементы из одной сети родственными, а из разных сетей адекватными, если они соответствуют одному элементу исходной сети. В сетях А и В родственные элементы образуют наборы из m(t) элементов. У каждой группы есть адекватная в другой сети. Будем считать, что элементы каждой сети пронумерованы двойными числами. Порядок нумерации определен нумерацией элементов на С (первая компонента номера) и нумерацией вводимых новых экземпляров С* (вторая компонента). Поэтому адекватные элементы сетей А и В образуют одинаковые номера, и можно говорить об адекватности по номеру для элементов с одинаковыми номерами. Функцию Теорема 4. Отказ сети селективного дублирования наступает только при тех конфигурациях отказов вершин графа, при которых наступает отказ соответствующей корпоративной системы. (Доказательство очевидно, поскольку изоморфное вложение полной задачи не может использовать отброшенные дуги полного графа: дуги между элементами этих типов в исходном графе отсутствуют.) Следствие. Вероятность отказа при селективном дублировании на любом такте не выше, чем на корпоративной сети с тем же составом элементов. Фазовый переход наработки по скорости роста в ИВС При реализации ИВС любым из методов дублирования для произвольной начальной ВС возникает эффект, аналогичный теоремам 1, 2 для корпоративных ИВС. Такие ИВС будем называть дублирующими. Для селективного дублирования это следует из теоремы 4. Для алгоритмов 1 и 2 доказательство требует специального анализа. Замечание 4. Рассмотрим корпоративную сеть с одним типом элементов. Отказ такой сети соответствует разрушению всех элементов, поскольку полная задача в этом случае может быть отображена в одну вершину полного графа. По той же причине отказ произвольной ВС с одним типом элементов соответствует отказу всех элементов. Определение 2. Макросетью для дублирующей ИВС назовем сеть, элементами которой являются экземпляры исходной ВС, составляющие ИВС, а граф связей элементов соответствует дугам между экземплярами сети. Для простого дублирования макросеть состоит из m(t) вершин без дуг. Для связного дублирования макросеть будет полным графом на m(t) вершинах. Все элементы макросети (макроэлементы) дублирующей ИВС имеют один тип – экземпляры исходной сети. Но у макроэлементов, кроме пары состояний «исправен/отказ», имеются промежуточные состояния частичного разрушения РВС. На этих состояниях есть вероятностная матрица переходов марковского процесса. В нашей постановке все вероятности в ней положительны и матрица конечная. Поэтому можно определить минимальную P¢ и максимальную P¢¢ вероятность перехода в «отказ» по всем предыдущим возможным состояниям. Аналогично имеются минимальная Q¢ и максимальная Q¢¢ вероятности перехода в одно из работоспособных состояний из состояния «отказ». Тогда по замечанию 4 макросеть имеет наработку не меньшую, чем корпоративная ИВС с одним типом элементов и вероятностями отказа и восстановления P¢,P¢¢ и Q¢,Q¢¢. Число элементов при этом равно m(t). При достаточно малом исходном значении p выполняется Замечание 5. Для непростого дублирования оценка наработки, полученная по замечанию 4, заведомо занижена, так как полная задача строится относительно исходной ВС, а не макросети. Поэтому возможно сохранение работоспособности ИВС при формальном отказе всех экземпляров исходной ВС. Для получения верхней оценки наработки требуется оценить сверху число возможных вложений исходной сети в расширенную сеть. Обозначим это число S(t). Тогда для простого дублирования S(t)=m(t). Для связного дублирования каждая связь продублирована не более чем Из замечания 5 и теорем 1, 2 следуют теоремы 5 и 6. Теорема 5. Пусть
то имеется положительная вероятность H безотказной работы корпоративной сети неограниченное время. Если выполнено условие
то с вероятностью 1 отказ сети наступит за конечное число тактов. Теорема 6. Если принять параметрический закон роста
Критическая скорость роста, ниже которой гарантировано, что отказ произойдет за конечное время, соответствует неравенству
По оценкам замечания 5 из (21) для разных типов дублирования получаем: - простое дублирование
- связное дублирование:
- селективное дублирование (N – число элементов исходной ВС):
Для разных типов дублирования величины Из доказанного видно, что неограниченное время безотказной работы ИВС возможно при логарифмическом росте по времени числа дублирующих экземпляров сети. Разумеется, при этом есть положительная вероятность отказа за конечное время. Коэффициент при логарифме должен быть не ниже указанного в (20). Различие между способами дублирования хорошо проявляется в оценке (21)–(24) для нижней критической скорости роста. Для методов дублирования со связями между экземплярами исходной сети оценка роста снижается до корня из логарифма времени. Однако при этом увеличивается методический интервал неопределенности критерия, поскольку полученная оценка верхней критической скорости не зависит явно от способа дублирования. Список литературы 1. Коганов А.В., Сазонов А.Н. Анализ отказоустойчивости вычислительной среды корпоративного типа. // Тр. Междунар. конф. – М.–Ижевск, НИЦ Регулярная и хаотическая динамика, 2006. – С. 228–234. 2. Коганов А.В., Сазонов А.Н. Корпоративные вычислительные сети с разрушением и восстановлением. Фазовый переход в растущих сетях.// Сб. науч. тр. – М.–Ижевск: НИЦ «Регулярная и хаотическая динамика». – 2007. – Т. 2. – С. 48–59. 3. Коганов А.В., Сазонов А.Н. Анализ критических точек отказоустойчивости вычислительной среды планетарного типа. // Программные продукты и системы. – 2007. – № 3. – С. 27–31. 4. Коганов А.В. Индукторные пространства как средство моделирования. // Вопросы кибернетики. – 1999. – С. 119–181. 5. Коганов А.В., Сазонов А.Н. Анализ отказоустойчивости вычислительной среды планетарного типа. // Тр. Междунар. конф. М. –Ижевск, НИЦ Регулярная и хаотическая динамика. – 2006. – С. 235–248. 6. Цициашвили Г.Ц., Маркова Н.В. Переходные явления в объединенной системе резервирования с восстановлением. // Дальневосточ. матем. журн. – 2001. – Т. 2. – № 2. – С. 106–114. |
| Permanent link: http://swsys.ru/index.php?id=1609&lang=en&page=article |
Print version Full issue in PDF (8.40Mb) |
| The article was published in issue no. № 4, 2008 |
Perhaps, you might be interested in the following articles of similar topics:
- Особенности модернизации центра обработки данных и космоцентра
- Модель надежности отказоустойчивого кластера с миграцией виртуальных машин
- Построение структуры предметной области на основе анализа концептуальной схемы
- Алгоритмическая основа генерации тестов с учетом радиационного воздействия
- Метод построения интерактивных систем мониторинга на основе гибких технологических процессов
Back to the list of articles
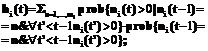

 (10b)
(10b)
 (15)
(15)