Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (Сибирский государственный аэрокосмический университет им. акад. М.Ф. Решетнева, г. Красноярск) - , Ph.D, Semenkin E.S. (styugin@rambler.ru) - Academician M.F. Reshetnev Siberian State Aerospace University, Krasnoyarsk, Russia, () - , Tynchenko V.S. (vadimond@mail.ru) - Academician M.F. Reshetnev Siberian State Aerospace University (Associate Professor), Krasnoyarsk, Russia, Ph.D | |
| Keywords: automatic projecting, , structural and parametrical synthesis, |
|
| Page views: 11598 |
Print version Full issue in PDF (4.72Mb) |
Искусственные нейронные сети (ИНС) успешно применяются для решения разнообразных научно-технических задач, таких как автоматизация процессов распознавания образов, адаптивное управление, аппроксимация функционалов, прогнозирование, создание экспертных систем, организация ассоциативной памяти и др. Однако эффективное применение на практике данного подхода широким кругом специалистов не всегда возможно из-за отсутствия формализованных процедур, полностью охватывающих весь процесс построения нейросетевых моделей. Разработанная программная система предназначена для автоматизации структурно-параметрического синтеза нейросетевой модели с произвольными связями между нейронами. Формализация процесса нейросетевого моделирования требует решения сложных многопараметрических оптимизационных задач выбора эффективной структуры нейросети и настройки ее весовых коэффициентов. При решении подобного рода задач оптимизации хорошо зарекомендовали себя генетические алгоритмы (ГА), которые не требуют информации о свойствах оптимизируемой функции и позволяют вести глобальный поиск в пространстве решений [1]. Выполнение расчетов по ГА требует значительных вычислительных ресурсов, однако указанные алгоритмы потенциально обладают свойством массового параллелизма при обработке информации, допуская их эффективную параллельную реализацию. Распараллеливание ГА на базе распределенной вычислительной системы позволяет существенно сократить время, затрачиваемое на решение задачи, за счет как параллельного выполнения вычислений, так и применения более эффективных, чем в последовательном случае, способов реализации алгоритмов [2]. Предлагаемая система автоматизации проектирования ИНС основана на комплексном применении разработанных авторами постановки многокритериальной задачи оптимизации структуры нейросетевой модели с учетом критерия минимизации вычислительной сложности этой структуры, а также нового многокритериального многопопуляционного параллельного ГА (ПГА). Формализованная постановка задачи многокритериальной оптимизации структуры ИНС выглядит следующим образом:
где C – матрица связей ИНС размерности Nн´Nн; W – матрица весов связей ИНС размерности Nн´Nн; Для структурно-параметрического синтеза нейросетевых моделей в программной системе используется разработанный авторами многокритериальный многопопуляционный ПГА с процедурой реструктуризации топологии связей между популяциями в ходе решения оптимизационной задачи. Данная процедура реализуется следующим образом: к выбранной базовой топологии связей между популяциями динамически добавляются временные связи между изолированными друг от друга популяциями, чтобы популяции, недостаточно хорошо функционирующие в текущий момент, могли получить дополнительных мигрантов из лучших индивидов тех популяций, которые показывают достаточно хорошие результаты. Приведем схему многокритериального многопопуляционного ПГА с реструктуризацией топологии связей между популяциями. Введем обозначения: N – количество популяций; mi – скорость миграции i-й популяции ( Рассмотрим работу алгоритма на примере l-й популяции. 1. Выполнить kl циклов многокритериального ГА. 2. Вычислить значения 3. Если 4. Выполнить миграцию в соответствии с полученной топологией.
При Разработанная программная система предоставляет пользователю возможности: − устанавливать и изменять в ходе работы программы параметры ГА при настройке весов связей ИНС, а также при выборе эффективной структуры ИНС (объем популяции, генетические операторы, количество итераций и т.д.); − устанавливать параметры ПГА (топологию связи между субпопуляциями, скорость и схему миграции, а также миграционный интервал); − отслеживать в ходе работы программной системы построение графиков пригодности лучшего и худшего индивидов популяции, а также средней пригодности популяции при настройке весов ИНС; − отслеживать в ходе работы программной системы количество недоминируемых индивидов популяции, а также построение графиков средней пригодности популяции и пригодности худшего индивида популяции при выборе эффективной структуры ИНС. Разработанная программная система была использована для выбора эффективной структуры ИНС, а также весов связей при решении практической задачи моделирования процесса рудно-термической плавки [3]. Размерность вектора входных воздействий на процесс и вектора выходных параметров равна 10. Для проведения экспериментов использовалась выборка из 47 точек. Вычислительные эксперименты проводились в сети из пяти однотипных персональных компьютеров с процессорами Athlon64 3200+. При решении задачи были выбраны следующие параметры многопопуляционного ПГА: размер популяции – 20 индивидов; количество поколений – 30; турнирная селекция (3 индивида в турнире); равноточечная рекомбинация; средняя мутация; максимальное количество скрытых нейронов – 10; скорость миграции – 2 индивида; синхронная миграция с интервалом в 3 поколения; схема миграции – для перемещения случайным образом отбираются недоминируемые индивиды; замещаются индивиды с наименьшим значением функции пригодности. В результате решения данной задачи была получена аппроксимация Парето-множества – множество из 16 нейросетевых моделей с ошибкой настройки от 3,42 до 3,74 % и вычислительной сложностью, лежащей в пределах от 357,04 до 369,27. Приближение фронта Парето на последнем поколении ГА показано на рисунке. Таким образом, полученные результаты свидетельствуют об эффективности применения предложенного модельно-алгоритмического и программного обеспечения к решению задач нейросетевого моделирования. Разработанная система автоматизации проектирования ИНС многокритериальными ПГА позволяет значительно ускорить процесс построения нейросетевых моделей, повысить их качество и предоставить возможность выбора нейросетевой модели из множества альтернатив, исходя из требуемой точности и имеющихся вычислительных ресурсов. Литература 1. Гладков Л.А., Курейчик В.В., Курейчик В.М. Генетические алгоритмы. М.: Физматлит, 2006. 320 с. 2. Cantu-Paz E. Designing scalable multi-population parallel genetic algorithms // IllGAL Report 98009. The University of Illinois, 1998, pp. 82–122. 3. Гонебная О.Е. Экспертная система рудно-термической плавки: дисс. … канд. технич. наук. Красноярск: ГУЦМиЗ, 2004. 136 с. |
| Permanent link: http://swsys.ru/index.php?id=2269&lang=en&page=article |
Print version Full issue in PDF (4.72Mb) |
| The article was published in issue no. № 2, 2009 |
Perhaps, you might be interested in the following articles of similar topics:
- Программная система структурно-параметрического синтеза системы защиты информации
- Программная реализация метода автоматизированного проектирования фюзеляжа воздушного судна с помощью объектно-ориентированных технологий
- Автоматизированное формирование персональных должностных инструкций сотрудников проектных организаций
- Модель расчета емкости автоматического склада продукции
Back to the list of articles

 – вектор активационных функций на нейронах в ИНС размерности Nн; Nн – количество нейронов в ИНС;
– вектор активационных функций на нейронах в ИНС размерности Nн; Nн – количество нейронов в ИНС;  – реальное значение k-го выхода ИНС, имеющей структуру
– реальное значение k-го выхода ИНС, имеющей структуру  , при подаче на ее входы j-го образа;
, при подаче на ее входы j-го образа;  – идеальное (желаемое) выходное состояние k-го нейрона; n – количество нейронов на выходе сети; m – размер обучающей выборки; Nсв – количество связей ИНС;
– идеальное (желаемое) выходное состояние k-го нейрона; n – количество нейронов на выходе сети; m – размер обучающей выборки; Nсв – количество связей ИНС;  – коэффициент относительной сложности вычисления активационной функции на i-м нейроне;
– коэффициент относительной сложности вычисления активационной функции на i-м нейроне;  – время вычисления активационной функции на i-м нейроне; Tсв – время обработки одной связи ИНС.
– время вычисления активационной функции на i-м нейроне; Tсв – время обработки одной связи ИНС.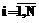 ); ki – период миграции i-й популяции (
); ki – период миграции i-й популяции ( ,
,  , показателей качества работы всех алгоритмов.
, показателей качества работы всех алгоритмов. , добавить временную связь от популяции j, для которой
, добавить временную связь от популяции j, для которой  , к популяции l с вероятностью
, к популяции l с вероятностью  , где
, где  .
. Качество работы параллельно функционирующих популяций оценивается в соответствии со следующим выражением:
Качество работы параллельно функционирующих популяций оценивается в соответствии со следующим выражением: , где
, где 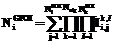 – количество глобально Парето-оптимальных индивидов в популяции i-го алгоритма;
– количество глобально Парето-оптимальных индивидов в популяции i-го алгоритма;  – количество Парето-оптимальных индивидов в популяции i-го алгоритма;
– количество Парето-оптимальных индивидов в популяции i-го алгоритма; 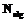 – количество параллельно функционирующих алгоритмов;
– количество параллельно функционирующих алгоритмов;  , где
, где  – i-й недоминируемый индивид j-го алгоритма;
– i-й недоминируемый индивид j-го алгоритма;  – метрика в пространстве индивидов.
– метрика в пространстве индивидов. :
:  , при
, при  :
:  , где k – коэффициент участия «плохих» алгоритмов.
, где k – коэффициент участия «плохих» алгоритмов.