Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Keywords: traffic flows, virtual reality, , modeling |
|
| Page views: 16183 |
Print version Full issue in PDF (4.72Mb) |
В современных условиях развития технологий виртуальной реальности значительно возросло число кибернетических систем, целью функционирования которых является имитация окружающего мира. Наиболее жесткие требования по реалистичности моделируемого окружения предъявляются к обучающим системам, используемым для отработки навыков специфических профессий. Тренажеры обучения вождению используют результаты компьютерного моделирования для их визуального отображения и воздействия на обучаемого – человека, проходящего обучение. Исследование, проведенное американским центром по контролю и предотвращению заболеваний, показало, что степень точности имитации окружающей обстановки является ключевым показателем при подготовке водителей на тренажерах вождения. Таким образом, к системам имитации дорожного движения, применяемым в обучении, предъявляются дополнительные требования по реалистичности создаваемого виртуального окружения. Основная проблема, возникающая при решении задачи имитации реалистичной дорожной обстановки, заключается в многоаспектности факторов, влияющих на ее восприятие обучаемым. Можно выделить следующие основные подзадачи, требующие решения [1]: - синтез реалистичной картины проезжей части; - синтез реалистичной динамики виртуального мира в условиях ограниченных вычислительных ресурсов; - синтез реалистичного поведения динамических объектов. Синтез реалистичного поведения динамических объектов позволяет обеспечить поведение участников дорожного движения, в высокой степени схожее с их поведением в реальном мире. Также необходимо обеспечить их адекватную реакцию на действия друг друга и действия обучаемого и возможность отработки сценариев для выполнения обучающих упражнений. Традиционно модели дорожного движения классифицируются по уровню детализации на макроскопические, микроскопические и мезоскопические. Использование разрабатываемых моделей в тренажерных обучающих системах с их последующей визуализацией требует детальной имитации отдельных участников движения, таким образом исключая из рассмотрения макроскопические модели. Применение микроскопических моделей обеспечивает в высокой степени точную имитацию динамики поведения участников дорожного движения. Недостатком является высокая ресурсоемкость процесса моделирования. В свою очередь, мезоскопические модели страдают от недостатка реалистичности поведения и взаимодействий при приемлемом уровне использования вычислительных ресурсов. Для решения поставленной задачи предлагается применить подход, объединяющий достоинства микроскопических и мезоскопических моделей. В частности, предлагается использование многоагентного подхода, теории стаи и клеточных автоматов в качестве микроскопических и мезоскопических моделей соответственно. Данный подход призван обеспечить процесс моделирования, удовлетворяющий ключевым показателям реалистичности и производительности. Абстрактный подход многоагентных систем (МАС) заключается в представлении рассматриваемой системы в виде множества агентов, существующих в едином окружении (среде) и взаимодействующих между собой для достижения определенных целей. Агентом можно называть любую программную или аппаратную сущность, которая способна воспринимать свою среду посредством перцепторов и воздействовать на нее посредством исполнительных механизмов для достижения некоторых целей [2]. Применение агентно-ориентированного подхода к области моделирования дорожного движения позволяет рассматривать всех участников дорожного движения как интеллектуальных агентов. Для рассмотрения агента в контексте конкретной области – моделировании дорожного движения – необходимо интерпретировать ряд свойств агента в терминах этой области: - общественное поведение – необходимость сосуществования с другими участниками дорожного движения; - реактивность – реакция на изменяющуюся дорожную обстановку (светофоры, пешеходы и другие участники дорожного движения); - адаптируемость – способность изменять маршрут или отменять маневр; - знания – знания агентом характеристик транспортного средства, правил дорожного движения и пр.; - убеждения – знания о положении и намерениях других транспортных средств, сигнале светофора и др.; - желания – состояния, характеризующиеся движением на безопасной дистанции, с определенной скоростью и др.; - намерения – намерения выполнить определенный маневр: перестроение, поворот и пр.; - цели – достижение промежуточной или конечной точки маршрута движения. Агента, обладающего перечисленными свойствами, назовем трафик-агентом. В соответствии с классификацией, предложенной в [3], область моделирования дорожного движения как среда функционирования агентов имеет следующие свойства. Частично наблюдаемая – водитель не имеет данных о том, какие маневры собираются выполнять другие водители. Стохастическая – невозможно точно предсказать поведение всех других участников движения. Последовательная – для выполнения маневра необходимо выполнить ряд последовательных взаимозависимых действий. Динамическая – при принятии решения водитель и другие участники движения продолжают движение. Непрерывная – скорость и местоположение водителя и других участников движения изменяются в определенном диапазоне и непрерывны с течением времени. Многоагентная – существует множество подобных транспортных средств, каждое из которых стремится прибыть в пункт назначения. Обладающая всеми перечисленными свойствами среда дорожного движения относится к классу наиболее трудномоделируемых сред. Функционирование агента в среде при условии соблюдения неких ограничений (правил дорожного движения) определяется парой , где Env – среда, а Y: R®{0,1} – предикат последовательности действий R агента Ag [2]. Тогда множество последовательностей действий агента Ag в среде Env, удовлетворяющих критерию Y, представляется в виде RY(Ag, Env)={r | rÎR(Ag, Env)ÙY(R)}. Таким образом, для имитации трафика, удовлетворяющего правилам дорожного движения, необходимо разработать программу трафик-агента, преобразующую его восприятия в действия, отвечающие поставленным критериям.
Разработка модели агента, помимо программы, функционирование которой отражено в его архитектуре, включает построение физической модели участника дорожного движения. Физическая модель имитирует динамику передвижения транспортного средства, схожую с динамикой в реальном мире. Таким образом, программа трафик-агента на каждом шаге выработки действия должна учитывать ограниченную возможность исполнения этих действий. Если считать, что скорость автомобиля является единственным параметром физической модели, то множество возможных воздействий записывается в виде Ac(v)={v*| ||v*|| Для организации взаимодействия между агентами можно применить аппарат теории стаи. Теория стаи, входящая в область исследования коллективного интеллекта, рассматривает вопросы самоорганизации многочисленных взаимодействующих динамических объектов. Несложность применяемых методов делает теорию пригодной для использования в различных областях: групповое передвижение роботов, анимация передвижения вооруженных сил и потоков людей, исследования поведения стай животных в природе и др. Применение теории стаи к области моделирования дорожного движения позволяет рассматривать транспортный поток как результат множества последовательных простых взаимодействий между участниками дорожного движения. На стаю в дорожном движении накладываются дополнительные ограничения. Перемещение членов стаи в пространстве ограничено рамками проезжей части текущего участка маршрута движения. При этом движение должно ориентироваться по направлению дороги, а расположение объектов согласовываться с полосами движения. Последнее может нарушаться в случае препятствий на проезжей части или затрудненного движения (затора). В свою очередь, правила локальных взаимодействий между соседними членами стаи должны подчиняться правилам дорожного движения. Можно выделить следующие типы поведения объектов в транспортном потоке [1]: - следование – согласование скорости объекта с соседними объектами; - - обгон – согласование скорости и направления движения для преодоления препятствия; - разъезд – согласование скорости и направления движения во избежание лобовых столкновений; - поперечное движение – согласование положения на проезжей части при движении в полосе и при выполнении маневров.
Модель КА представляет собой дискретную динамическую систему, состоящую из следующих частей: КА=(L, Σ, N, δ), где L – физическое окружение, представленное дискретной решеткой; Σ – множество возможных состояний клетки; N – частично упорядоченное множество смежных клеток; δ – локальное правило перехода. Каждая i-я клетка решетки в момент t находится в состоянии
Состояние i-й клетки на шаге t+1 вычисляется с помощью правила δ на основе состояний смежных клеток в момент времени t, где |N| – количество смежных клеток. При применении концепции КА к моделированию дорожного движения физическое окружение представляет собой дорогу, по которой движутся автомобили. В классической однополосной реализации КА дорожное полотно представляется в виде одномерной решетки. Пример пространственно-временной динамики классического КА приведен на рисунке 1, где две автомашины, i и j, движутся по одномерной решетке. Представлены конфигурации КА в последовательные моменты t и t+1. Типичная дискретизация модели подразумевает, что ∆T=1 cек., а ∆X=7,5 м, что соответствует изменению скорости ∆V=∆X/∆T=27 км/ч. Единицы дискретизации были выбраны исходя из средней длины автомобиля на дороге и среднего времени реакции водителя. Движение отдельного участника в дорожном потоке описывается набором правил, которые отражают его поведение при следовании и перестроении. В КА для этого используется локальное правило перехода, задающее передвижение машин по мере того, как сам автомат эволюционирует с течением времени. Таким образом, в классической постановке состояние системы изменяется посредством синхронных пересчетов позиций всех участников. Для каждого автомобиля вычисляется новая скорость, после чего пересчитывается его позиция исходя из новой скорости и возможного маневра при смене полосы. Существует и другой механизм изменения состояния автомата, который заключается в случайном последовательном пересчете. Пример интеграции микроскопических и мезоскопических моделей на участке дороги показан на рисунке 2. Совокупное использование перечисленных моделей позволяет обеспечить процесс моделирования, удовлетворяющий ключевым требованиям реалистичности и производительности. Данный подход был использован при разработке программного комплекса тренажеров вождения, обеспечивающего подготовку водителей маршрутных транспортных средств. Тренажеры вождения автобуса ЛиАЗ-5256, разработанные производственной фирмой «ЛОГОС» (г. Москва), успешно функционируют на учебно-курсовом комбинате Мосгортранс. Литература 1. Olstam J.J., Lundgren J., Adlers M., Matstoms P. A framework for simulation of surrounding vehicles in driving simulators. ACM transactions on Modeling and Computer Simulation. 2008. Vol. 18. № 3. pp. 1–24. 2. Wooldridge M. An Introduction to multiagent systems. Chichester, England: John Wiley & Sons, 2002. 348 p. 3. Рассел С., Норвинг П. Искусственный интеллект: современный подход; пер. с англ. М.: Вильямс, 2006. 2-е изд. 1408 с. 4. Low K.H., Leow W.K., Ang M.H. A hybrid mobile robot architecture with integrated planning and control. Proceeding of the international joint conference on Autonomous Agents and Multiagent Systems. Bologna, Italy, 2002. pp. 219–226. 5. Van den Berg J., Lin M., Manocha D. Reciprocal velocity obstacles for real-time multi-agent navigation. Proceedings of the 2008 IEEE International Conference on Robotics and Automation. 2008. pp. 1928–1935. |
| Permanent link: http://swsys.ru/index.php?id=2290&lang=en&page=article |
Print version Full issue in PDF (4.72Mb) |
| The article was published in issue no. № 2, 2009 |
Perhaps, you might be interested in the following articles of similar topics:
- Информационно-вычислительная система моделированияи прогнозирования торфяных пожаров
- Алгоритм и программа расчета напряженно-деформированного состояния песчаных грунтов при циклическом нагружении
- Моделирование информационных процессов систем управления большими данными для решения задач кибербезопасности
- Моделирование оптимальных условий биосинтеза
- Разработка и исследование гибридного метода генетического программирования
Back to the list of articles
 В свою очередь, архитектура агента определяет, как будет построена компьютерная система, удовлетворяющая определенным свойствам трафик-агента. В условиях городской обстановки агент сталкивается с непредвиденными пространственно-временными событиями внешнего мира и другими агентами. В обоих случаях он должен адекватно реагировать и принимать решения, поэтому архитектура должна позволять ему справляться с неопределенностью и неполнотой информации и реагировать на непредвиденные события, пользуясь относительно простыми правилами. Данным требованиям удовлетворяет класс гибридных архитектур [4], сочетающий достоинства архитектур, основанных на знаниях (делиберативных) и на поведении (реактивных) [2]. Часть архитектуры, основанная на знаниях, решает задачу планирования передвижений по городу. Реактивная составляющая определяет поведение агента в сложившейся неопределенной дорожной ситуации. Явно выделяются следующие функциональные блоки реактивной компоненты: блок достижения поставленной точки маршрута, блок движения без столкновений и блок межагентного взаимодействия. Инвариантными по отношению к применяемым концепциям построения архитектур являются модуль глобальной модели мира и модуль, реализующий характерные особенности поведения агента.
В свою очередь, архитектура агента определяет, как будет построена компьютерная система, удовлетворяющая определенным свойствам трафик-агента. В условиях городской обстановки агент сталкивается с непредвиденными пространственно-временными событиями внешнего мира и другими агентами. В обоих случаях он должен адекватно реагировать и принимать решения, поэтому архитектура должна позволять ему справляться с неопределенностью и неполнотой информации и реагировать на непредвиденные события, пользуясь относительно простыми правилами. Данным требованиям удовлетворяет класс гибридных архитектур [4], сочетающий достоинства архитектур, основанных на знаниях (делиберативных) и на поведении (реактивных) [2]. Часть архитектуры, основанная на знаниях, решает задачу планирования передвижений по городу. Реактивная составляющая определяет поведение агента в сложившейся неопределенной дорожной ситуации. Явно выделяются следующие функциональные блоки реактивной компоненты: блок достижения поставленной точки маршрута, блок движения без столкновений и блок межагентного взаимодействия. Инвариантными по отношению к применяемым концепциям построения архитектур являются модуль глобальной модели мира и модуль, реализующий характерные особенности поведения агента.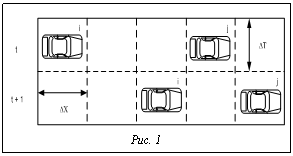 перестроение – согласование скорости и направления движения для межполосного перемещения;
перестроение – согласование скорости и направления движения для межполосного перемещения;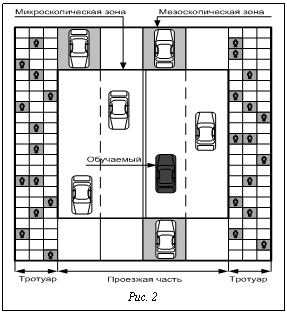 Использование микроскопических моделей, отражающих точные динамические характеристики участников движения, на всей области имитации дорожного движения невозможно вследствие их повышенной ресурсоемкости. В последние годы сформировалось направление, использующее интеграцию клеточных автоматов (КА) и МАС, где первое используется в качестве физической модели, служащей основой для модели верхнего уровня, определяющей поведение отдельного водителя. Применение подобных мезоскопических моделей в обучающих системах ограничено из-за недостаточно реалистичной динамики. Наиболее эффективной является имитация пешеходных и транспортных потоков на основе клеточного автомата на определенном удалении от обучаемого.
Использование микроскопических моделей, отражающих точные динамические характеристики участников движения, на всей области имитации дорожного движения невозможно вследствие их повышенной ресурсоемкости. В последние годы сформировалось направление, использующее интеграцию клеточных автоматов (КА) и МАС, где первое используется в качестве физической модели, служащей основой для модели верхнего уровня, определяющей поведение отдельного водителя. Применение подобных мезоскопических моделей в обучающих системах ограничено из-за недостаточно реалистичной динамики. Наиболее эффективной является имитация пешеходных и транспортных потоков на основе клеточного автомата на определенном удалении от обучаемого. , а смежные с ней клетки решетки есть Ni(t). Тогда локальное правило перехода представляется в виде
, а смежные с ней клетки решетки есть Ni(t). Тогда локальное правило перехода представляется в виде .
.