Планирование процессов обработки потока запросов в распределенных вычислительных системах (РВС) осуществляется исходя из цели, архитектуры вычислительной системы и модели потока запросов. Существует множество методов планирования, отличающихся целью, используемыми моделями РВС и потоками запросов, а также алгоритмами распределения ресурсов. Эффективность использования существующих методов планирования в большой степени зависит от их соответствия области применения. Основной задачей при планировании является обеспечение требуемого качества предоставляемых услуг по обработке запросов пользователей. Для этого необходимо выбрать и применить оптимальный для конкретной области метод планирования. Наличие множества различных по эффективности альтернатив обусловливает сложность выбора. Снижение оперативности, простой ресурсов в результате неоптимального выбора определяют особую актуальность задачи оценивания методов планирования процессов обработки запросов в РВС.
 При сравнительной оценке методов планирования широко применяется моделирование процесса обработки запросов в РВС, в том числе с использованием полунатурных моделей. Согласно работе [1], для оценивания методов планирования необходимы модели вычислительной системы, входного потока запросов и системы планирования. В настоящее время существуют полунатурные модели РВС и систем планирования, которые могут использоваться при исследовании процесса обработки запросов. Кроме того, есть адекватные модели потоков запросов для имитационных систем моделирования, например, в системах SimGrid, OptorSim. Полунатурные модели, представленные в виде генераторов нагрузки, не обладают требуемой для оценивания методов планирования точностью, что приводит к необходимости разработки новой модели для каждой исследуемой РВС. Отсутствие полунатурных моделей с требуемой адекватностью и значительные потери при необоснованном выборе метода планирования определяют особую актуальность задачи разработки полунатурной структурно и параметрически настраиваемой модели потока запросов в РВС.
При сравнительной оценке методов планирования широко применяется моделирование процесса обработки запросов в РВС, в том числе с использованием полунатурных моделей. Согласно работе [1], для оценивания методов планирования необходимы модели вычислительной системы, входного потока запросов и системы планирования. В настоящее время существуют полунатурные модели РВС и систем планирования, которые могут использоваться при исследовании процесса обработки запросов. Кроме того, есть адекватные модели потоков запросов для имитационных систем моделирования, например, в системах SimGrid, OptorSim. Полунатурные модели, представленные в виде генераторов нагрузки, не обладают требуемой для оценивания методов планирования точностью, что приводит к необходимости разработки новой модели для каждой исследуемой РВС. Отсутствие полунатурных моделей с требуемой адекватностью и значительные потери при необоснованном выборе метода планирования определяют особую актуальность задачи разработки полунатурной структурно и параметрически настраиваемой модели потока запросов в РВС.
К модели предъявляются следующие требования:
– адекватность, определяемая возможностью настройки структуры модели и ее параметров по критерию пригодности в соответствии с требованиями эксперимента по выбору метода планирования;
– обеспечение повторяемости реализаций моделей потоков запросов, а также взаимодействия с различными системами планирования.
Поток запросов L состоит из последовательности запросов. При этом он является случайным и представляет собой последовательность событий, наступающих в случайные промежутки времени. Событием является факт поступления запроса пользователей в РВС для обработки. Каждый запрос QÎL требует выделения ресурсов из их ограниченного множества. Для оценивания метода планирования предлагается использовать модель потока запросов  , которая генерируется системой генерации G из исходной гибкой модели потока запросов F(L) путем ее структурной и параметрической настройки:
, которая генерируется системой генерации G из исходной гибкой модели потока запросов F(L) путем ее структурной и параметрической настройки:
 , (1)
, (1)
где S – структурная, P – параметрическая настройка исходной модели; G – генерация полунатурной модели.
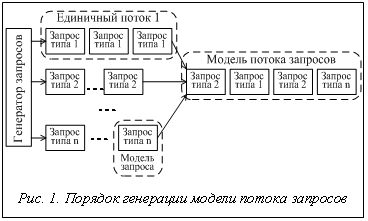
Предлагается моделировать поток запросов с использованием концептуальной модели следующего вида (рис. 1):
 , (2)
, (2)
 , (3)
, (3)
где PL – параметры модели потока запросов; F(li) – параметрически и структурно настраиваемая модель потока однотипных запросов (единичный поток); n – количество единичных потоков в модели; r – связи между потоками. Количество параметров может изменяться экспериментатором в зависимости от условий. Обоснованность выделения потоков однотипных запросов определяется работой [2], в которой указывается, что для большинства вычислительных систем набор из порядка десяти потоков однотипных запросов определяет 85–90 % вычислительной нагрузки.
Каждая модель единичного потока формируется на основе модели запроса, образующего поток, и параметров потока:
 , (4)
, (4)
 , (5)
, (5)
где  – параметры модели i-го единичного потока; F(Qi) – модель запроса; i – интенсивность поступления запросов; g – вид закона распределения времени между поступлениями запросов; {pg} – параметры закона распределения; w – закон изменения интенсивности. Список параметров модели настраивается экспериментатором в зависимости от условий проведения экспериментов.
– параметры модели i-го единичного потока; F(Qi) – модель запроса; i – интенсивность поступления запросов; g – вид закона распределения времени между поступлениями запросов; {pg} – параметры закона распределения; w – закон изменения интенсивности. Список параметров модели настраивается экспериментатором в зависимости от условий проведения экспериментов.
Модель запроса описывается кортежем вида
 , (6)
, (6)
где x=x(t) – требования по своевременности обработки запроса; R – объективная ресурсоемкость запроса, определяющая совокупность требований к ресурсам различного типа; l – объем запроса (входных данных). Ресурсоемкость запроса R описывается кортежем вида
 , (7)
, (7)
где v – вычислительная ресурсоемкость; op – объем требуемой оперативной памяти; net – требуемый сетевой ресурс; arch. – требуемая архитектура вычислительного узла; m – количество одновременных потоков; po – требуемое программное обеспечение (системное и прикладное).
Предлагается генерировать полунатурную модель  путем формирования потока полунатурных моделей запросов (рис. 2) системой генерации полунатурных моделей G. Полунатурная модель запроса FПН(Q) будет реализовываться в виде гибкой вычислительной задачи, которая представляет собой программу, потребляющую ресурсы в соответствии с настройками. Программа запускается как в последовательном, так и в параллельном режиме. Настройки текущего экземпляра программы передаются одновременно с самой программой. В результате прогнозирования параметров потока и образующих единичные потоки запросов на основе исходной модели запроса генерируется текущий вариант полунатурной модели
путем формирования потока полунатурных моделей запросов (рис. 2) системой генерации полунатурных моделей G. Полунатурная модель запроса FПН(Q) будет реализовываться в виде гибкой вычислительной задачи, которая представляет собой программу, потребляющую ресурсы в соответствии с настройками. Программа запускается как в последовательном, так и в параллельном режиме. Настройки текущего экземпляра программы передаются одновременно с самой программой. В результате прогнозирования параметров потока и образующих единичные потоки запросов на основе исходной модели запроса генерируется текущий вариант полунатурной модели  путем ее настройки. После настройки параметров и структуры образующих запросов задаются настройки единичных потоков. Единичные потоки выделяются путем проведения кластерного анализа исходной выборки. Объединение сгенерированных единичных потоков
путем ее настройки. После настройки параметров и структуры образующих запросов задаются настройки единичных потоков. Единичные потоки выделяются путем проведения кластерного анализа исходной выборки. Объединение сгенерированных единичных потоков 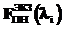 образует полунатурную модель
образует полунатурную модель  , требуемую для проведения экспериментов по выбору метода планирования. Период генерации потока устанавливается экспериментатором. Адекватность полунатурной модели определяется возможностью гибкой настройки модели путем определения ее структуры и параметров. Повторяемость реализаций модели потока запросов предлагается обеспечивать путем сохранения настроек всех сгенерированных моделей запросов. Для взаимодействия с различными системами планирования используются полунатурные модели запросов с настраиваемыми экспериментатором служебными заголовками.
, требуемую для проведения экспериментов по выбору метода планирования. Период генерации потока устанавливается экспериментатором. Адекватность полунатурной модели определяется возможностью гибкой настройки модели путем определения ее структуры и параметров. Повторяемость реализаций модели потока запросов предлагается обеспечивать путем сохранения настроек всех сгенерированных моделей запросов. Для взаимодействия с различными системами планирования используются полунатурные модели запросов с настраиваемыми экспериментатором служебными заголовками.
 Для практической реализации предлагаемой гибкой полунатурной модели был разработан прототип системы генерации, состоящий из сервера генерации и программы, реализующей полунатурную модель запроса. (Программа DataFlowModelGenerator защищена свидетельством о государственной регистрации программ для ЭВМ № 2009614467 / И.В. Логинов, Е.В. Лебеденко.) Прототип сервера генерации реализован на языке высокого уровня С++ для работы в среде Windows.
Для практической реализации предлагаемой гибкой полунатурной модели был разработан прототип системы генерации, состоящий из сервера генерации и программы, реализующей полунатурную модель запроса. (Программа DataFlowModelGenerator защищена свидетельством о государственной регистрации программ для ЭВМ № 2009614467 / И.В. Логинов, Е.В. Лебеденко.) Прототип сервера генерации реализован на языке высокого уровня С++ для работы в среде Windows.
Прототип полунатурной модели запроса может использоваться в операционных системах Windows и Linux. Он позволяет обеспечивать требуемую интенсивность потребления ресурсов различных типов: коммуникационных, вычислительных и оперативной памяти в соответствии с заданными настройками. Перспективой развития сервера генерации моделей потоков запросов является его реализация на языке сценариев для обеспечения возможности использования на вычислительных узлах с различной архитектурой. Интенсивность потребления ресурсов вычислительного узла моделью запроса определяется файлом настроек, формируемым сервером генерации для каждого запроса. Такой файл представляет собой документ типа XML, в котором содержатся все настройки модели запроса.
Согласно алгоритму на рисунке 2 была разработана полунатурная модель потока запросов к распределенному почтовому серверу, состоящему из двух вычислительных узлов. В процессе анализа входного потока в нем были выделены три единичных потока, образованных почтовыми запросами разного типа. С использованием прототипа сервера генерации настроена модель  и осуществлена генерация полунатурной модели
и осуществлена генерация полунатурной модели  . Анализ результатов обработки полунатурной модели потока запросов на узлах сервера показал ее адекватность для выбора метода планирования.
. Анализ результатов обработки полунатурной модели потока запросов на узлах сервера показал ее адекватность для выбора метода планирования.
В результате исследований предложена гибкая параметрически и структурно настраиваемая модель потока запросов, предназначенная для использования при анализе систем планирования процессов обработки запросов в РВС. Предложенный алгоритм генерации позволяет получать полунатурную модель потока запросов с требуемой для проведения экспериментов адекватностью путем настройки гибкой исходной модели с использованием сервера генерации.
Литература
1. Проблемы моделирования GRID-систем и их реализации // О.И. Самоваров [и др.] // Научный сервис в сети Интернет: решение больших задач: тр. Всеросс. науч. конф. (22–27 сентября 2008 г., Новороссийск). М.: Изд-во МГУ, 2008. 468 с.
2. Ларионов А.М., Майоров С.А., Новиков Г.И. Вычислительные комплексы, системы и сети. Л.: Энергоатомиздат, 1987. 288 с.
 При сравнительной оценке методов планирования широко применяется моделирование процесса обработки запросов в РВС, в том числе с использованием полунатурных моделей. Согласно работе [1], для оценивания методов планирования необходимы модели вычислительной системы, входного потока запросов и системы планирования. В настоящее время существуют полунатурные модели РВС и систем планирования, которые могут использоваться при исследовании процесса обработки запросов. Кроме того, есть адекватные модели потоков запросов для имитационных систем моделирования, например, в системах SimGrid, OptorSim. Полунатурные модели, представленные в виде генераторов нагрузки, не обладают требуемой для оценивания методов планирования точностью, что приводит к необходимости разработки новой модели для каждой исследуемой РВС. Отсутствие полунатурных моделей с требуемой адекватностью и значительные потери при необоснованном выборе метода планирования определяют особую актуальность задачи разработки полунатурной структурно и параметрически настраиваемой модели потока запросов в РВС.
При сравнительной оценке методов планирования широко применяется моделирование процесса обработки запросов в РВС, в том числе с использованием полунатурных моделей. Согласно работе [1], для оценивания методов планирования необходимы модели вычислительной системы, входного потока запросов и системы планирования. В настоящее время существуют полунатурные модели РВС и систем планирования, которые могут использоваться при исследовании процесса обработки запросов. Кроме того, есть адекватные модели потоков запросов для имитационных систем моделирования, например, в системах SimGrid, OptorSim. Полунатурные модели, представленные в виде генераторов нагрузки, не обладают требуемой для оценивания методов планирования точностью, что приводит к необходимости разработки новой модели для каждой исследуемой РВС. Отсутствие полунатурных моделей с требуемой адекватностью и значительные потери при необоснованном выборе метода планирования определяют особую актуальность задачи разработки полунатурной структурно и параметрически настраиваемой модели потока запросов в РВС. , которая генерируется системой генерации G из исходной гибкой модели потока запросов F(L) путем ее структурной и параметрической настройки:
, которая генерируется системой генерации G из исходной гибкой модели потока запросов F(L) путем ее структурной и параметрической настройки: , (1)
, (1) , (2)
, (2) , (3)
, (3) , (4)
, (4) , (5)
, (5) – параметры модели i-го единичного потока; F(Qi) – модель запроса; i – интенсивность поступления запросов; g – вид закона распределения времени между поступлениями запросов; {pg} – параметры закона распределения; w – закон изменения интенсивности. Список параметров модели настраивается экспериментатором в зависимости от условий проведения экспериментов.
– параметры модели i-го единичного потока; F(Qi) – модель запроса; i – интенсивность поступления запросов; g – вид закона распределения времени между поступлениями запросов; {pg} – параметры закона распределения; w – закон изменения интенсивности. Список параметров модели настраивается экспериментатором в зависимости от условий проведения экспериментов. , (6)
, (6) , (7)
, (7) путем ее настройки. После настройки параметров и структуры образующих запросов задаются настройки единичных потоков. Единичные потоки выделяются путем проведения кластерного анализа исходной выборки. Объединение сгенерированных единичных потоков
путем ее настройки. После настройки параметров и структуры образующих запросов задаются настройки единичных потоков. Единичные потоки выделяются путем проведения кластерного анализа исходной выборки. Объединение сгенерированных единичных потоков 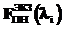 образует полунатурную модель
образует полунатурную модель 
 и осуществлена генерация полунатурной модели
и осуществлена генерация полунатурной модели 