Journal influence
Bookmark
Next issue
Model of the elementary particles accelerator
The article was published in issue no. № 2, 2010Abstract:Today the Accelerator of Ideal elementary Particles (AIP) is created in Russia which allows already to receive experimental acknowledgement or disproof of existing fundamental physical theories supposed to answer the most secret questions of mankind. The feature of this accelerator is its sizes. It can be placed inside computer that allows to turn existing submissions about accelerators as the most expensive and bulky machines which the mankind ever created for checking theories.
Аннотация:В России создан ускоритель идеальных элементарных частиц, позволяющий уже сегодня получать эксперимен-тальные подтверждения или опровержения существующих фундаментальных физических теорий, призванных ответить на волнующие человечество вопросы. Особенностью этого ускорителя являются его размеры. Он умещается в компьютере, что позволяет перевернуть существующие представления об ускорителях как самых дорогостоящих и громоздких машинах, которые когда-либо создавались для проверки теорий.
| Authors: (gan56@mail.ru) - , Ph.D, (md_net@mail.ru) - | |
| Keywords: computer modeling, elementary particle accelerator |
|
| Page views: 12102 |
Print version Full issue in PDF (4.97Mb) Download the cover in PDF (1.38Мб) |
Внимание ученых-физиков всего мира приковано к новому сверхмощному ускорителю элементарных частиц, так называемому большому адронному коллайдеру (БАК) (Large Hadron Collider – LHC), запущенному в Европейском центре ядерных исследований [1]. Интерес к вводу этого гигантского сооружения (кольцо ускорителя по периметру составляет чуть меньше 30 км) вызван прежде всего тем, что, по мнению большинства ученых, сторонников этого проекта, он поможет дать ответ на фундаментальные вопросы физики, в частности, откуда появляется именно такая масса, которую мы получаем в экспериментах, позволит проверить достаточное количество теоретических (в основном математических) конструкций. К таким абстрактным конструкциям можно отнести нашумевшие в последнее время теорию великого объединения, теорию суперструн и всевозможные ее модификации, правильную квантовую теорию поля, включающую гравитационное, и многие другие. Теории – это представления, выведенные в виде некоторых текстов. Практически любой важный не только для небольшого количества специалистов, занимающихся данной тематикой, но и для каждого человека вопрос может быть поставлен следующим образом: существует ли какой-либо реальный процесс, стоящий за всеми математическими абстракциями, теориями, и как его можно смоделировать, не прибегая к таким дорогостоящим конструкциям, каковой является БАК. Известно, что даже при успешной работе коллайдера для получения ответов на вопросы, поставленные физиками, потребуется не менее 10 лет. А ответы на вопросы, касающиеся всех людей, – вообще туманная перспектива. Поэтому желательно было бы иметь альтернативу коллайдеру. Как только появились компьютеры, возникла мысль об альтернативных способах работы с физикой. Тем более, что сами объекты исследования (частицы, в частности протоны) и продукты их столкновений (еще более мелкие частицы) никто никогда не видел и не увидит: с промежутков времени, измеряемых в аттосекундах (10-18 сек.), ничего увидеть невозможно, все наши представления являются либо математическими, либо компьютерными моделями. В свое время Р. Фейнман высказал идею, которую назвал моделированием физики на компьютерах [2]. Однако попытки ее реализации не привели к желаемому результату. Так, машины клеточных автоматов, идея разработки которых была высказана сотрудниками Исследовательского центра IBM Р. Ландауэром и Ч. Беннетом, а также первые специализированные машины клеточных автоматов Тоффоли так и остались машинами, позволяющими решать некоторые практические задачи. Все чаще они вспоминаются скорее как курьез, чем серьезное начинание, точнее, серьезная альтернатива существующим способам моделирования и экспериментальных проверок. Кроме этого, предпринимаются активные попытки визуализации частиц и процессов, происходящих на микроуровне [3]. Компьютерное моделирование прочно заняло свое место в физике. Однако это не более чем красивые анимации, так как не предоставляют возможности получать данные, имеющие хоть какое-то отношение к достигнутым в реальных экспериментах. Эти анимации строятся на основе данных, полученных либо математическими расчетами, либо экспериментально, но не по явлениям, смоделированным в компьютерных системах. Понятие «идеальные частицы» было введено Р. Фейнманом [4] в его знаменитых лекциях. Идеальный электрон, идеальный фотон – это некая математическая конструкция, абстракция, существующая в интуиции человека как нечто и позволяющая полуаналитическим (с использованием математических зависимостей), полуграфическим методом (методом вращающихся стрелок) определять n и j, то есть аналог массы и аналог заряда. Однако из его же слов следует, что идеальных частиц не существует. Отсюда и трудности перехода от полученных n и j к реальным m – массе и e – заряду частиц. Метод, по которому удалось все-таки осуществить этот переход, был назван методом перенормировки, который Р. Фейнман не оценил как строгое в математическом плане решение вопроса, понимая, что в физике микромира есть некая фундаментальная непонятность. Так что же было сделано для того, чтобы можно было заявить о создании ускорителя идеальных частиц? Опишем логический путь, который привел к возможности создания такого ускорителя. Сегодня, как известно, строгим научным методом вывода существующих в сознании представлений (идей), включая идеи, появляющиеся в интуиции, является математика с ее абстракциями. Интуиция – это данная природой естественная способность строить собственные представления об окружающем мире и о нас самих. Математика занимается исключительно формальным описанием либо процессов, сопровождающих порождение представлений, либо конкретных представлений, порожденных этой природной способностью [5]. Идеальная частица – это тоже некоторая идея, абстрактная структура, существующая в сознании человека. Как известно, естественным носителем любых идей является человек со своими способностями, то есть человек – это иерархическая структура способностей. С другой стороны, для описания свойств и в конечном счете визуализации объектов, существующих в микромире как что-то целое, кроме математических, других сколько-нибудь эффективных методов не существует. Это означает, что сами объекты микромира являются не чем иным, как носителями человеческих способностей, причем начиная с простейших – способностей быть. Именно этим можно объяснить широкое распространение так называемого мысленного эксперимента при изучении микромира. Назовем все частицы способностями, например, оставлять свои следы. Это определение будет точным и для электронов, и для фотонов, и прочих частиц, так как в экспериментах по исследованию микромира и мира частиц в качестве так называемых сырых результатов или данных, кроме следов от них, ничего не получается. Таким образом, если создать нечто, обладающее способностью оставлять свои следы, и если в дальнейшем механизм этого нечто будет соответствовать лежащему в основе реализации человеческих способностей, начиная от способностей быть до способностей мыслить, то можно получить именно то, что сегодня называется частицами. Если такое нечто создать, например, в компьютере, то останется проверить, будет ли оно при его экспериментальном исследовании давать те же результаты, что получаются на столь дорогостоящих ускорителях. Такова логика постановки задачи на построение компьютерной системы, обладающей собственными способностями (КСС) [6]. Суть подхода, реализованного в виде КСС, в следующем. Прежде всего под способностью понималось множество потенциальных возможностей, возможных действий. В основе их реализации лежит супервзаимодействие, рассматриваемое как элементарное взаимодействие (на уровне атрибутов), сторонами которого уже являются взаимодействия. Именно этот факт непосредственно связывает построенную КСС с физикой, с проблемами поиска хиггс-механизма в физике, наделяющего, по предположению физиков, частицы стандартной модели (СМ) массами. Способность рассматривалась как появляющееся эмерджентное свойство на реально организованном в компьютерной среде супервзаимодействии. С математикой КСС объединяет то, что в основе любых математических формализмов также лежит способность иметь собственные представления и понятия, называемые математическими абстракциями. Необходимо отметить, что математика в процессе своей эволюции часто возвращается к основам множества, подтвержение этому – постоянные попытки обобщений. Результатом таких обобщений, как правило, являются очень простые системы и понятия. Есть и другой подход выстраивания математических теорий на основе постулатов и аксиом, которые вводятся априори в качестве так называемых неопределяемых простейших понятий и определений. В силу дуалистичности способности как таковой (в основе которой лежит супервзаимодействие) в математике часто наблюдаются прямо противоположные подходы к решению одних и тех же проблем или определению одних и тех же понятий, а точнее, самой способности иметь собственные понятия. Одним из таких примеров является определение Б. Риманом и К. Вейерштрассом функции в рамках теории функций комплексной переменной, в конечном итоге они просто более полно рассматривают саму способность порождать и выстраивать сложные математические конструкции, порождать математические понятия. К таковым относятся элемент функции Á(z-a) и аналитический образ Вейерштрасса (аналитическая функция), являющийся сложной конструкцией из нескольких рядов, связанных путем их аналитических продолжений, имеющих общие области их кругов сходимости, а также функция комплексного переменного Римана f(z), где z=x+iy – комплексное число; значение самой функции также является комплексным числом, но уже с другими переменными w=u+iv. Такие функции должны удовлетворять так называемым условиям Коши–Римана, выраженным в предположении непрерывности и дифференцируемости следующими уравнениями с частными производными:
Таким образом, если сегодня принципиально невидимые как целое объекты, такие как частицы, могут быть выражены только путем записи математических уравнений, то КСС, визуализируя сами процессы, которые обеспечивают возможность получения этих уравнений, визуализируют частицы как целое. По сути КСС позволяет не только изучать свойства и характеристики ранее принципиально невидимых объектов, но и проводить с ними эксперименты. Так, на рисунке 1 продемонстрирован эксперимент по определению спектра атомной структуры. В окне слева показан аналитический образ Вейерштрасса, или аналитическая функция Римана. В верхнем окне справа выводится спектр данных, генерируемых аналитическим образом, полученный с использованием преобразования Фурье. В нижней части окна показана возможность получения графиков любых характеристик данного явления. В связи с тем, что функции, выводимые в виде визуальных образов, могут стать многозначными (выражаясь словами Римана, многолистными), КСС позволяет записывать и проигрывать истории проведенных экспериментов, снимая эту неоднозначность. (Известно, что в экспериментах на реальных коллайдерах следы частиц часто и очень быстро замазывают результаты предыдущих измерений, что является большой проблемой и лишний раз подтверждает идентичность процессов, протекающих в ускорительных экспериментах и в экспериментах, проводимых в КСС.) КСС, обладая понятием «частица», позволяет проводить самые различные эксперименты с ними. На фрагменте процесса взаимодействия двух частиц (рис. 2) показано образование, которое в физике имеет название глюбол, но еще ни разу не полученное экспериментально. В разработанной КСС это явление действительно получается и действительно «висит в пространстве» рядом с основным процессом взаимодействия. Оно получено в КСС экспериментально. Это означает, что можно определить все необходимые для возникновения этого явления значения параметров. Достаточно перенести их на реальный ускоритель с учетом масштабов. Именно на этом основана возможность использования КСС в качестве ускорителя идеальных элементарных частиц. КСС обеспечивает возможность и позволяет визуализировать сами абстракции частиц на уровне понятий о них. Кроме этого, она позволяет организовывать различные взаимодействия между такими частицами и получать результаты этих взаимодействий. Результаты экспериментальных исследований могут не только наблюдаться, но и измеряться в привычных для человека пространстве и времени. Количественные данные, полученные при проведении экспериментов с таким ускорителем, могут подвергаться различным видам обработки, в том числе с построением графиков значений интересующих переменных, таблиц, зависимостей, с применением привычных в подобных экспериментах математических аппаратов.
На основе КСС предлагается разработать не лабораторный, а полномасштабный ускоритель элементарных частиц как инструмент, позволяющий существенно повысить эффективность проведения экспериментов на реальных ускорителях, а может быть, и существенно пересмотреть подобные программы в сторону их удешевления или скорейшего получения искомых ответов. Литература 1. URL: http://elementy.ru/LHC/news (дата обращения: 18.01.2010). 2. Фейнман Ричард П. Department of physics, California Institute of Technology, Pasadena. California. 3. Visualizing the kinematics of relativistic wave packets. Bernd Thaller Institute for Mathematics and Scientific Computation, University of Graz Heinrichstrasse 36, A-8010 Graz, Austria. 4. Фейнман Р. Ф 36 КЭД – странная теория света и вещества; пер. с англ. М.: Наука. Глав. ред. Физматлит, 1988. 144 с. 5. Вигнер Юджин. Этюды о симметрии; пер. с англ. Ю.А. Данилова; под ред. Я.А. Смородинского. М.: Мир, 1971. 6. Васильев Н.Г. Математическая модель псевдоорганизма. КАУС – путь к созданию искусственного интеллекта. Т. 1. № 4. 1996. С. 37–42. Сознание и физическая реальность (Естествознание). |
| Permanent link: http://swsys.ru/index.php?id=2526&lang=en&page=article |
Print version Full issue in PDF (4.97Mb) Download the cover in PDF (1.38Мб) |
| The article was published in issue no. № 2, 2010 |
Perhaps, you might be interested in the following articles of similar topics:
- Программа расчета пропускной способности гибких производственных ячеек
- Алгоритмы автоматизированной системы управления испытанием оборудования на надежность
- Компьютерное моделирование для интеллектуальной оценки динамического взаимодействия твердых тел
- Концепция математического и компьютерного моделирования тепловых процессов в электронных системах
- Метод испытания радиолокационных станций с использованием беспилотного летательного аппарата и бортового оборудования
Back to the list of articles
 , следствием из них является Du=0; Dv=0. Заметим, здесь, как и в идеальных частицах по Р. Фейнману, имеются четыре различные переменные – x, y, u, v (у Фейнмана – n, j, m, e). Так вот Р. Фейнман реализовал процесс – рисование вращающихся стрелочек, который в принципе обеспечивал возможность получения уравнений Коши–Римана. А так как Коши и Риман наверняка не рисовали никаких вращающихся стрелочек, то аналогичные процессы просто протекали в их сознании при выведении или понимании этих уравнений. Таким образом, получается, что Р. Фейнман просто предложил верный процесс, который в каком-то отношении оказался эквивалентным сопровождающим мышление механизмам. Для использования метода Р. Фейнмана человек должен был непрерывно рисовать все эти вращающиеся стрелочки для получения результата. Однако Р. Фейнман не усмотрел в своем методе связи с представлениями Римана и Вейерштрасса. В разработанной КСС реализовано длящееся в пространстве и времени супервзаимодействие как носитель механизма, обеспечивающего существование переменных и операций, связывающих их в геометрическом виде, полностью соответствующих уравнениям Коши–Римана. Получается, что это не просто уравнения, записанные на бумаге, а существующие, в отличие от представлений человека, скрытых в сознании или интуиции, непосредственно видимые понятия и представления, обеспечивающие получение этих уравнений. Поэтому наблюдение этого процесса в виде символьных обозначений или же собственно процессов становится делом вкуса или привычки. Этот пример с идеальными частицами Р. Фейнмана и представлениями о функции комплексного переменного Римана и Вейерштрасса приведен лишь для иллюстрации того, что реализовано в КСС.
, следствием из них является Du=0; Dv=0. Заметим, здесь, как и в идеальных частицах по Р. Фейнману, имеются четыре различные переменные – x, y, u, v (у Фейнмана – n, j, m, e). Так вот Р. Фейнман реализовал процесс – рисование вращающихся стрелочек, который в принципе обеспечивал возможность получения уравнений Коши–Римана. А так как Коши и Риман наверняка не рисовали никаких вращающихся стрелочек, то аналогичные процессы просто протекали в их сознании при выведении или понимании этих уравнений. Таким образом, получается, что Р. Фейнман просто предложил верный процесс, который в каком-то отношении оказался эквивалентным сопровождающим мышление механизмам. Для использования метода Р. Фейнмана человек должен был непрерывно рисовать все эти вращающиеся стрелочки для получения результата. Однако Р. Фейнман не усмотрел в своем методе связи с представлениями Римана и Вейерштрасса. В разработанной КСС реализовано длящееся в пространстве и времени супервзаимодействие как носитель механизма, обеспечивающего существование переменных и операций, связывающих их в геометрическом виде, полностью соответствующих уравнениям Коши–Римана. Получается, что это не просто уравнения, записанные на бумаге, а существующие, в отличие от представлений человека, скрытых в сознании или интуиции, непосредственно видимые понятия и представления, обеспечивающие получение этих уравнений. Поэтому наблюдение этого процесса в виде символьных обозначений или же собственно процессов становится делом вкуса или привычки. Этот пример с идеальными частицами Р. Фейнмана и представлениями о функции комплексного переменного Римана и Вейерштрасса приведен лишь для иллюстрации того, что реализовано в КСС. С одной стороны, разработанная КСС еще достаточно проста для моделирования сложных способностей человека, например, говорить на естественном языке или переводить тексты с одного языка на другой, однако это больше ее достоинство, чем недостаток в силу того, что в физике микромира сегодня как раз и надо проявить элементарные начала. С другой стороны, она достаточно сложна, чтобы позволять проводить с ней эксперименты с получением данных, подобных тем, которые сегодня получаются при исследовании микромира. Если для человека, который является, пожалуй, самым сложным для него же самого комплексом способностей, понять и увидеть самые элементарные способности – слишком сложная задача, то для разработанной КСС, обладающей своими элементарными способностями, которые по механизму их реализации аналогичны человеческим, такая задача является элементарной, а точнее сказать, естественной.
С одной стороны, разработанная КСС еще достаточно проста для моделирования сложных способностей человека, например, говорить на естественном языке или переводить тексты с одного языка на другой, однако это больше ее достоинство, чем недостаток в силу того, что в физике микромира сегодня как раз и надо проявить элементарные начала. С другой стороны, она достаточно сложна, чтобы позволять проводить с ней эксперименты с получением данных, подобных тем, которые сегодня получаются при исследовании микромира. Если для человека, который является, пожалуй, самым сложным для него же самого комплексом способностей, понять и увидеть самые элементарные способности – слишком сложная задача, то для разработанной КСС, обладающей своими элементарными способностями, которые по механизму их реализации аналогичны человеческим, такая задача является элементарной, а точнее сказать, естественной.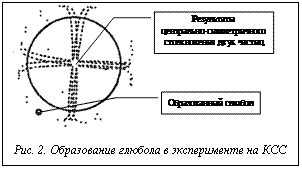 Короче говоря, физик-экспериментатор будет ощущать себя во вполне привычных условиях. Только в отличие от настоящих он практически отработает методики перехода к реальным частицам, атомам, молекулам и веществам. Физик-теоретик не будет зависеть от запуска сверхмощного и сверхдорогого ускорителя для определения верности своего решения. Он способен самостоятельно проверить свои теоретические выкладки, проводя многочисленные эксперименты, не выходя из дома.
Короче говоря, физик-экспериментатор будет ощущать себя во вполне привычных условиях. Только в отличие от настоящих он практически отработает методики перехода к реальным частицам, атомам, молекулам и веществам. Физик-теоретик не будет зависеть от запуска сверхмощного и сверхдорогого ускорителя для определения верности своего решения. Он способен самостоятельно проверить свои теоретические выкладки, проводя многочисленные эксперименты, не выходя из дома.