Software & Systems

Товарные запасы торговых предприятий имеют основной удельный вес в стоимости их активов, являются главным источником пополнения собственных средств за счет прибыли от реализации и вместе с тем создают большую проблему ежедневного контроля. В России оптимизация запасов на уровне торговых предприятий, обеспечивающая максимальный уровень обслуживания потребителей при минимальных инвестициях в запасы, минимальных затратах на заказ и транспортировку, пока осуществляется, как правило, методом проб и ошибок. Для управления запасами используется системный подход, то есть запасы рассматриваются во взаимосвязи с различными сторонами деятельности фирмы. В настоящее время актуальным является применение научного управления запасами, что сокращает стихийные регуляторы этого процесса [1].

В статье рассматриваются задачи управления товарными запасами в системе складов на предприятиях розничной торговли. К логистическим задачам управления товарными запасами можно отнести определение оптимального уровня запасов на всех складах торговой сети, объемов и сроков поставок, выбор лучших поставщиков, контроль уровня товарных запасов и автомати- ческая подготовка проектов заказов на их пополнение [2].

Для определения оптимального уровня запасов на всех складах торговой сети решаются подзадачи: пополнение запасов региональных складов с центрального склада, перераспределение товарных запасов между региональными складами с целью увеличения продаж, выбор лучших поставщиков и заказ товара у них.

Запасы региональных складов пополняются с центрального склада ритмичными еженедельными поставками или по его указанию со складов изготовителей. Поставляемые партии комплектуются на основе предложений центрального склада по номенклатуре и количеству, подтвержденными региональными складами.

Управление товарными запасами в системе складов (филиалов)

ЛПР (товаровед, директор магазина и т.п.) получает рекомендации системы поддержки принятия решений (СППР) относительно того, какой товар лучше добавить в поставку филиалу для быстрой реализации. ЛПР посылает запрос системе учета товара по сбору статистической информации из своих баз и/или хранилищ данных. Эти данные передаются СППР, которая выдает рекомендации по управлению в приемлемом для пользователя виде.

Очевидно, что использование естественного языка со всем набором имеющихся в нем выразительных средств для рассуждений и принятия решений с помощью качественных представлений, понятий и оценок типа «мало», «много», «редко», «часто» и т.д. позволяет всесторонне и компактно описать общую смысловую постановку задач управления. Целесообразность и продуктивность такого подхода для решения задач управления подтверждается рядом практических разработок (см., например, [3]).

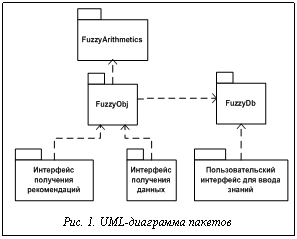
На рисунке 1 представлена диаграмма пакетов СППР, в которые сгруппированы классы и методы, позволяющие использовать методы нечеткой логики, работать с лингвистическими переменными и нечеткой арифметикой.

Класс, реализующий логический вывод, наиболее удачно описан в пакете FuzzyObj, который взаимосвязан с пакетом FuzzyArithmetics, где реализованы функции фаззификации, дефаззификации, вычисления расширенной Т-нор­мы, Т-конормы, сравнения нечетких множеств, арифметические операции над нечеткими переменными, имеющими числовую интерпретацию, и с пакетом Fuzzy­Db, в котором осуществляются доступ к знаниям, хранящимся в БЗ, и манипулирование ими.

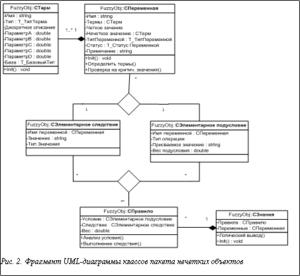
На рисунке 2 представлен фрагмент статической структуры пакета FuzzyObj в терминологии классов объектно-ориентированного программирования, приведены классы, реализующие функции и поведение объектов, участвующих в логическом выводе. Термы задаются в системе функциями принадлежности, имеющими предопределенный вид: П-, S-, Z-образные. Переменные могут быть входящими, исходящими, промежуточными, а также лингвистического, логического или числового типов.

При управлении товарными запасами выделим следующие критерии: складские остатки в филиалах, значимость филиалов в распределении выбранной товарной позиции, продажи выбранной товарной позиции в филиалах, количество товара, подлежащего распределению/пере­распределению, стоимость доставки партии из филиала в филиал в случае перераспределения и прибыльность высвобождаемых средств.

Эксперт формулирует ряд правил, которые можно записать согласно поддерживаемой системой структуре:

Правило ::= 'IF' Условие 'THEN' заключение ['WITH' вес_правила] ';'

Условие ::= (подусловие | Имя_переменной) { 'AND' (подусловие | имя_переменной)}

Подусловие ::= имя_переменной 'IS' имя_терма ['WITH' вес_подусловия]

Заключение ::= (подзаключение) { 'AND' (подзаключение)}

Подзаключение ::= (имя переменной | имя_переменной 'IS' имя_терма | Арифм_выраж)| внешняя_функция {'AND' ( имя_переменной | (имя_переменной 'IS' имя_терма) | Арифм_выраж ) | внешняя_функция }

Арифм_выраж ::= (имя_переменной | имя_терма) арифметическая_операция (имя_переменной | имя_терма) {арифметическая_операция (имя_переменной| имя_терма) арифметическая_операция (имя_переменной | имя_терма)}

Арифметическая_операция ::= +|-|*|/

Вес_правила ::= 0..1

Вес_подусловия ::= 0..1

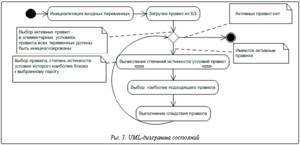
Логический вывод в сети таких правил организуется в СППР и носит циклический характер (рис. 3). Для выбора наиболее подходящего правила следует сравнить истинность условия правила с заданным значением лингвистической переменной, которая определяется полнотой покрытия правилами БЗ данной предметной области. Она определена на интервале [0,1] и может принимать значения «удовлетворительно», «безупречно» и т.п. На основании этого сравнения принимается решение о выполнении следствия правила, причем при означивании переменных, определенных в следствии, степень истинности того, что переменная принимает заданное значение, становится равной степени истинности условия правила [4].

Так, согласно представленной структуре для задачи распределения товарных ресурсов могут быть сформулированы правила следующего типа:

ЕСЛИ Остатки_филиала_i= «Низкие» [важность «Высокая»] И Важность_филиала_i= «Высокая» И Продажи_филиала_i = «Высоке» И Количество_товара_для_рас­пределения >0 ТО INC(Количество_товара_ для _фили­ала_i ) И DEC(Количество_товара_для_распределения ) И DEC(Важность_филиала_i ) [вес_правила = Высокий]

ЕСЛИ Остатки_филиала_1 = «Норма» И Остатки_фи­лиала_2 = «Норма» … И Остатки_филиала_N = «Норма» ТО РАСПРЕДЕЛИТЬ_СОГЛАСНО_ПРОДАЖАМ

Где РАСПРЕДЕЛИТЬ_СОГЛАСНО_ПРОДАЖАМ – внешняя функция.

Для решения задачи перераспределения товарных ресурсов между филиалами пример правила, по которому может приниматься решение о перемещении товара из филиала в филиал, следующий:

ЕСЛИ Остатки_на_филиале_доноре_i = «больше нормы» И Остатки_на_филиале_доноре_i = «больше среднего кол-ва по складам» И Остатки_на_филиале_реципиенте_j = «меньше нормы» И Остатки_на_филиале_реципиенте_j = «меньше среднего кол-ва по складам» И Прибыльность_от_высвобождаемых средств = «высокая» ТО «Выбрать Q наиболее подходящих изделий для перемещения» И INC(Остатки_на_филиале_реципиенте_j , Q) И DEC(Ос­татки_на_филиале_доноре_i ,Q)

Необходимо отметить, что каждому параметру, выбранному в качестве регулирующего товарные запасы, должно соответствовать либо количественное, либо качественное значение. Во втором случае требуется построить функции принадлежности терм-множеств лингвистической переменной в разрезе каждого товара или групп, принятых к учету. При большой номенклатуре построение соответствующих функций принадлежности затруднительно. Для автоматизации этого процесса использовался метод построения функций принадлежности по накопленным статистическим наблюдениям исходя из распределения данных. Метод основан на кластеризации [5], с помощью которой синтезируют функции принадлежности при экстракции нечетких моделей.

Литература

1.   Добронравин Е.Р. Организация системы управления запасами // Genobium, 2006. URL: http://www.genobium.com/ r/a28_thesis.htm (дата обращения: 20.11.2009).

2.   Волгин В.В. Склад: организация, управление, логистика. М.: Издат.-торг. корпор. «Дашков и К», 2005.

3. Прикладные нечеткие системы; под ред. Т. Тэрано, К. Асам, М. Сугено. М.: Мир, 1993.

4. Синюк В.Г., Пивненко Е.В. Применение нечеткой истинности в логическом выводе, основанном на активации сети

продукций // Интеллектуальные системы (AIS'07); Интеллектуальные САПР (CAD-2007): тр. Междунар. науч.-технич. конф. В 4-х т. М.: Физматлит, 2007. Т. 2. С. 221–223.

5. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику // Консультационный центр Matlab компании Softline, 2006. URL: http://matlab.exponenta.ru/fuzzylogic/book1/ index.php (дата обращения: 15.12.2009).