Journal influence
Bookmark
Next issue
Fuzzy search of proper names using lk-representations
The article was published in issue no. № 3, 2010Abstract:For fuzzy search of proper names in special bases of personal data the technique of fuzzy words comparison and search is proposed based on lk-representations. This technique guarantees matching of words with fixed degree of relative distortions.
Аннотация:Для решения задачи нечеткого поиска именных групп в специализированных базах персональных данных предложен метод нечеткого сравнения и поиска слов с использованием их lk-представлений, обеспечивающий гарантированное нахождение соответствий, характеризуемых заданной степенью искажений.
| Authors: Bondarenko A.V. (bond@fgosniias.ru) - Moscow Institute of Physics and Technology (Professor), Dolgoprudny, Russia, Ph.D, (viz@GosNIIAS.ru) - , Ph.D, (info@gosniias.ru) - , Ph.D, (klyshinsky@itas.miem.edu.ru) - , Ph.D | |
| Keywords: lk-representations, levenshtein distance, fuzzy search |
|
| Page views: 13645 |
Print version Full issue in PDF (5.84Mb) Download the cover in PDF (1.43Мб) |
При организации поиска именных групп (ИГ) в базах персональных данных возникают характерные проблемы, связанные с наличием в запросах орфографических и фонетических ошибок, ошибок ввода информации, а также с отсутствием единых стандартов транскрипции с иностранных языков. Вследствие указанных причин задача поиска в базах данных, содержащих ИГ, не может быть в полной мере решена только методами проверки на точное соответствие, в связи с чем становится актуальной задача разработки специальных методов и технологий нечеткого поиска. В настоящее время методы нечеткого поиска применяются для решения таких задач, как текстовый и мультимедийный поиск, поиск гомологических цепочек макромолекул в молекулярной биологии, поиск в графах и т.д. Однако универсальной методики их решения не существует, поскольку каждая проблема имеет собственную оригинальную специфику. В данной работе предлагается специализированный метод нечеткого поиска фамильно-именных групп, предназначенный для применения в автоматизированных информационных системах, содержащих персональные данные. Под нечетким поиском понимается поиск по ключевым словам с учетом возможных произвольных ошибок в написании ключевого слова или, напротив, ошибок написания слова в целевом запросе. Достаточно полный и подробный обзор современных методов поиска можно найти, например, в [1]. Основными аспектами организации текстового поиска являются способ построения поискового индекса, выбор поисковой метрики и собственно алгоритмы нечеткого поиска. Структуры данных информационного поиска, как правило, относятся к одной из двух основных групп: векторные и кластерные модели либо модели на основе ключевых слов. Основная идея векторных методов состоит в том, что считаются заданными m поисковых слов и каждый поисковый объект отображается в вектор, называемый профилем, причем величина k-го элемента профиля зависит от частоты вхождения в документ k-го поискового слова, например, слова, строки или подстроки длиной n символов (n-граммы). Поисковое выражение также рассматривается как документ с соответствующим профилем, и ключевым моментом организации поиска является выбор функции корреляции профилей. В выборку попадают документы, для которых корреляционное значение превышает пороговое. Недостатком векторных методов является необходимость считывания профилей всех документов. Устранить этот недостаток можно, разбив все документы на группы (кластеры) и определив в каждом кластере характерного представителя (центроид кластера), что позволяет сначала сравнивать поисковый запрос лишь с центроидами кластеров. В случае релевантности центроида запросу поиск продолжается далее внутри кластера, причем процесс разбиения выборки на кластеры может быть иерархическим (многоуровневым). При поиске по ключевым словам, как правило, осуществляют выборку всех документов, содержащих хотя бы одно ключевое слово, а затем ранжируют результаты поиска по релевантности. В основе поиска по ключевым словам лежит использование специализированных индексных словарей двух основных типов. Инвертированный файл (ИФ) – множество пар <ключевое слово, адрес вхождения ключевого слова в документ>. Сигнатурные файлы (СФ) содержат сигнатуры данных, представляющие собой их упрощенные профили, в которых каждый элемент кодируется одним битом. Сжатые ИФ существенно превосходят СФ по производительности для коротких запросов, но проигрывают им на длинных и очень длинных запросах. Ключевым элементом организации нечеткого поиска является выбор меры сходства слов или обратной функции – функции расстояния между словами, часто называемой метрикой даже в тех случаях, когда она не является метрикой в строгом математическом смысле. Наибольшее распространение здесь получили трансформационные метрики, в области текстового поиска называемые также расстояниями редактирования. Наиболее известны поисковые метрики следующих типов. Расстояние Хемминга между словами одинаковой длины определяется как число позиций, в которых символы не совпадают. Расстояние Левенштейна [2], позволяющее сравнивать слова различной длины, равно минимальному числу операций преобразования одного слова в другое, причем допустимы только операции вставки, удаления и замены, которым присвоена единичная стоимость. При определении расстояния Дамерау–Левенштейна перестановка символов принимается за единую операцию редактирования с весом 1. Известны меры сходства Джаро и Джаро–Уинклера [3], представляющие собой нормированные коэффициенты, специально разработанные для сравнения коротких строк, например, компонентов ИГ. Также получили распространение метрики, основанные на подсчете количества общих подстрок равной длины (n-грамм). Большинство практических алгоритмов по- иска ключевого слова в словаре основаны на модификациях одного из известных методов: последовательный поиск (полный перебор всех слов словаря), метод расширения выборки (query extension), метод n-грамм, поиск с использованием хеширования, методы на основе неравенства треугольника (триангуляционные деревья). Последовательный поиск предполагает последовательный перебор слов из словаря и сравнение каждого из них с запросом в соответствии с принятой метрикой. Данный метод применяется, например, в системах Agrep и Glimpse. Метод расширения выборки предполагает построение множества всевозможных ошибочных слов, например, получающихся из исходного в результате одной операции редактирования Левенштейна, после чего построенные поисковые запросы ищутся в словаре на точное совпадение. Метод широко используется в программах проверки орфографии, например Ispell, и часто связан с применением морфологического анализа, в частности стемминга. Метод n-грамм основан на том, что для поиска слов строится инвертированный файл, в котором роль документов играют слова, а роль слов – подстроки длины n, называемые n-граммами. Поиск с использованием хеширования состоит в подборе отображения (хеш-функции) слова, например, во множество чисел или строк, сохраняющего основные характеристики исходного слова и устойчивого к наиболее распространенным ошибкам. Известным примером является хеш-функция Soundex, встроенная в коммерческие СУБД Sybase, MS SQL Server, Oracle. Триангуляционные деревья позволяют индексировать множества произвольной структуры при условии, что на них задана метрика (необязательно евклидова). В основу построения триангуляционных деревьев положена идея расположения близких в смысле заданной метрики объектов в одинаковых поддеревьях. При поиске в текстовых массивах данный метод менее эффективен, чем при поиске в базах изображений или больших документов. Рассмотрим конкретную задачу нечеткого поиска фамильно-именных групп. Пусть имеется алфавит A={a1,a2,a3,…as}, |A|=s,s>1 – любое конечное множество символов. Слово w в алфавите A длины n определяется как конечная последовательность символов алфавита A: w=, wiÎA, i=1, ..., n. Словарем именных компонент U назовем заданное конечное множество слов, определенных на алфавите A: U={u1, u2, u3, …, um}, |U|=m, m³1. С учетом этого рассматриваемая в работе задача может быть формально поставлена следующим образом. Дано: слово-образец w, словарь U, целое k>0 и функция расстояния d, являющаяся метрикой. Требуется найти все j, такие, что d(w, uj)£k, ujÎU, где d – расстояние Левенштейна, определяемое как минимальное количество операций замены, вставки и удаления символов, необходимых для преобразования одного слова в другое. При этом необходимо построить алгоритм поиска, который вычислительно был бы более эффективен, чем метод полного перебора элементов словаря. Метод нечеткого сравнения и поиска слов с использованием lk-представлений Рассмотрим известный метод n-грамм, применяемый при решении подобных задач, в котором подстрока длины n слова w= называется n-граммой слова w. Обозначим множество всех n-грамм слова w как Nn(w). Идея использования n-грамм в задачах нечеткого сравнения слов такова. Если слово v похоже на слово u, то у них должны быть общие подстроки. Следовательно, если расстояние Левенштейна между v и u не превышает k: d(v, u)£k, причем ||Nn(u)||>k и ||Nn(v)||>k, то ||Nn(u)ÇNn(v)||³1, где норма множества определяется как количество его элементов. Принципиальным недостатком системы на основе классических n-грамм является чувствительность к выбору параметров (длина n-граммы, выбор порога фильтрации k). Кроме того, критерии отождествления, вычисляемые на основе n-грамм, зависят не только от расстояния Левенштейна, но и от расположения несовпадающих символов в сравниваемых словах, что недопустимо в задачах поиска ИГ. Для преодоления указанных недостатков перейдем от n-грамм к более полным представлениям слов. Введем следующие обозначения: − w Å v – результат конкатенации слов w и v; − w(w,t,l) – оператор выделения подстроки длины l из слова w, начинающейся c символа в позиции t; − e(w,t)=w(w,1,t-1) Å w(w,t+1,l-t) – оператор удаления из слова w символа в позиции t; − d(w,t,a)=w(w,1,t-1) Å a Å w(w,t+1,l-t) – оператор вставки в слово w символа a в позиции t; − m(w) – длина (число символов) слова (w). Введем ряд новых понятий и определений. Пусть нормировочным алфавитом ANR для алфавита A называется любой алфавит, такой, что ANRÇA=Æ. l-нормализованным словом для слова w называется слово wl*=w(w Å a,1,l), где a – нормировочное слово длины ||ANR||, содержащее все символы алфавита ANR в лексикографическом порядке, причем ||ANR||³l. lk-граммой слова w для фиксированных целых неотрицательных значений l и k называется последовательность символов, определяемая по индукции следующим образом: − l0-граммой слова w длины является l-нормализованное слово wl0=wl*; − l1-граммой слова w является слово wl1(i)= =e(wl0,i): iÎ{1,..,l}; − lk-граммой слова w " l³k>1 является слово wlk(i)=e(wlk-1(j),i): iÎ{1,..,l-k-1}, jÎ{1,..,l-k}. При этом параметры l и k имеют смысл длины нормализованного слова и допустимой степени искажения соответственно. Для фиксированных l и k множество всех lk-грамм слова w называется lk-представлением слова и обозначается Nlk(w), а множество всех lk-грамм слов, входящих в состав словаря U, называется lk-представлением словаря и обозначается Nlk(U): Nlk(U)= Функцией lk-принадлежности подстроки v слову w называется функция clk(w,v) = lk-спектром подстроки v по словарю U называется вектор Slk(w,U)=: uiÎNlk(U), i=1, ..., m, где m=||Nlk(U)||. Показателем lk-корреляции слов w и v по словарю U называется скалярное произведение их спектров: rlk(w,v)=(Slk(w,U),Slk(v,U))= где mNU=||Nlk(U)||. Скалярное произведение здесь понимается стандартно как сумма покомпонентных произведений векторов. При этом для произвольных w и uÎU выполняется следующее соотношение 0£rlk(w,u)£rmax(l,k)=rlk(u,u). Это позволяет определить соответствующую нормированную характеристику близости двух слов в пространстве lk-представлений. Нормированным коэффициентом lk-корреляции слов w и v по словарю U назовем коэффициент Klk(w,v)=rlk(w,v)/rmax(l,k). Относительно его свойств доказано следующее утверждение. Утверждение. Пусть даны два слова w и u, рассматривается словарь U={u}, l>max(m(w), m(u)) и l>k³0. Тогда нормированный коэффициент lk-корреляции Klk(w,u) обладает свойствами: 1) "w: 0£Klk(w,u)£1; 2) Klk(u,u)=1; 3) "w: Klk(w,u)=0Þd(w,u)>k, где d – расстояние Левенштейна. Доказательство. Свойства 1 и 2 следуют из определения. Докажем свойство 3, эквивалентное тому, что d(w,u)£k Þ rlk(w,u)>0. Перейдем к l-нормированным строкам wl* и ul*. Если l>max(m(w),m(v)), то легко показать, что каждое из элементарных преобразований слова (перечислены ниже) всегда может быть представлено эквивалентной комбинацией (суперпозицией) пары операций удаления и вставки символов: − удаление символа в позиции t: d(e(wl*,t),l,#), где #ÎANR; − вставка символа a в позиции t: d(e(wl*,l), t,#), где #ÎANR; − замена символа в позиции t на символ b: d(e(wl*,t),t,b); − перестановка пары соседних символов a и b: d(e(wl*,t),t+1,a); − тождественное преобразование также может быть представлено операциями фиктивного удаления и фиктивной вставки нормировочных символов конце слова: d(e(wl*,l),l,#), где #ÎANR. Пусть последовательность элементарных преобразований, переводящая слово w в слово u, содержит не более k элементарных преобразований перечисленных типов. Представим каждое из этих преобразований парой операций вставки и удаления, как показано выше. Отсортируем преобразования таким образом, чтобы сначала осуществлялись все вставки, а затем – все удаления. Получаем последовательное объединение двух цепочек однотипных преобразований (вставок и удалений), каждая из которых содержит не более k преобразований. Дополняем обе цепочки фиктивными преобразованиями таким образом, чтобы в общей последовательности оказалось в точности k удалений и k вставок. Поскольку описанные эквивалентные преобразования цепочек элементарных преобразований слова можно сделать всегда, то из условия d(wl*,ul*)£k следует существование последовательности из k вставок {ei: i=1,…,k} и k удалений {di: i=1,…,k}, такой, что: v1=e1(wl*), v2=e2(v1),…,vk=ek(vk-1), vk+1=d1(vk),…,v2k-1=dk-1(v2k-2), ul*=dk(v2k-1). Отсюда vkÎNlk(w) и vkÎNlk(u). Таким образом, Nlk(w)ÇNlk(u)¹ÆÞrlk(w,u)>0, что и требовалось доказать. Данное утверждение позволяет сформулировать численный критерий lk-отождествимости слов w и uÎU: Klk(w,u)³Kmin(l,k,x), где Kmin(l,k,x) – минимально допустимое значение нормированного коэффициента lk-корреляции, рассматриваемое как функция от максимально допустимого расстояния x=d(w,u) при фиксированных l и k. При этом важно, что формула для вычисления Kmin(l,k,x) может быть получена в явном виде. Для описанной рекурсивной процедуры построения lk-грамм справедлива оценка максимального показателя lk-корреляции: rmax(l,k)=k!Сlk, где Сlk = rlk(w,u)=r(l,k,x)= Таким образом, Klk(w,u)=rlk(w,u)/rmax(l,k)= = Полученную оценку порогового значения lk-корреляции можно проиллюстрировать следующими простыми примерами. Пусть l=7, k=3, x=1. Тогда Kmin(l,k,x)= Пусть l=7, k=2, x=1. Тогда Kmin(l,k,x)= Таким образом, как следует из всего вышесказанного, задача сравнения слов может быть решена с использованием описанного математического аппарата lk-представлений. Для проведения нечеткого поиска в словаре требуется предварительная подготовка данных, которая заключается в построении lk-представления словаря (индексного файла). При этом добавление информации о каждом новом словарном слове требует построения lk-представления данного слова и занесения соответствующих lk-грамм в lk-представление словаря. Для каждой добавленной lk-граммы хранятся ссылки на все слова, в lk-представлениях которых она встречалась. Алгоритм нечеткого поиска тестового слова в подготовленных данных состоит из трех основных этапов. 1. Вычисление lk-представления тестового слова. 2. Голосование lk-грамм тестового слова в пользу слов-гипотез из словаря. 3. Подсчет числа голосов и сравнение их с пороговым значением. Вычисление rlk(w,uj), ujÎU, реализуется на втором этапе алгоритма как процедура голосования всех lk-грамм wlk(i) слова w в пользу слов uj с весами, равными clk(uj,wlk(i)). На третьем этапе полученная суммарная оценка rlk(w,uj) для всех ujÎU сравнивается с порогом rmin(l,k,x), соответствующим Kmin(l,k,x). Оценка вычислительной сложности данного алгоритма имеет порядок O(||Nlk(w)||*ln(||Nlk(U)||)), что существенно эффективнее алгоритмов прямого поиска в словаре. Метод нечеткого сравнения и поиска многокомпонентных именных групп с использованием lk-представлений
Показателем lk-корреляции ИK w по МИГ U назовем rlk(w,U)=maxj rlk(w,uj). Пусть ИК w считается успешно отождествленной на МИГ U с точностью x, если rlk(w,U)³r(l,k,x). Показателем lkx-сходства qlkx(W,U) назовем количество ИК МИГ W, успешно отождествленных с точностью x на МИГ U. МИГ W будем считать успешно отождествленной с МИГ U с точностью x, если qlkx(W,U)³qmin, qmin£n. Данное выражение описывает критерий lkx-отождествимости многокомпонентных ИГ. Если бы при словарном поиске выполнялось непосредственное попарное сравнение ИК двух МИГ, то вычисление показателя сходства qlkx(W,U) не составляло бы проблемы. Для этого потребовалось бы, помимо словаря ИК, создать еще один словарь МИГ, размер которого чрезвычайно велик, как и время поиска в нем. Однако требования достижения большей вычислительной эффективности приводят к необходимости одновременного голосования всех компонент МИГ W в пользу всех компонент МИГ U, что делает нетривиальной задачу вычисления показателя сходства qlkx(W,U). Сформулируем ее математически. Суммарным показателем lk-корреляции МИГ W по МИГ U назовем rlk(W,U) = åi åj rlk(wi,uj). Данная статистика вычисляется для МИГ в целом на основе lk-представлений отдельных ИК. При этом " w,u: rlk(w,u)Îr, где r= – заранее известный набор значений, которые могут принимать показатели lk-корреляции отдельной ИК при фиксированных l и k. Значит, вне зависимости от числа отдельных компонент и того, как они отождествляются, суммарный показатель lk-корреляции всегда может быть представлен в следующем виде: rS=åt=0,..,l-1 qt´rt, где rS=rlk(W,U); rt=r(l,k,t)Îr; qt³0 – количество ИК МИГ W, отождествленных на U с точностью t. Отсюда искомый показатель lkx-сходства может быть определен по формуле qlkx(W,U)=åt=0,..,x qt. Таким образом, чтобы проверить критерий lkx-отождествимости, необходимо для вычисленного по запросу суммарного показателя сходства rS при заранее известном наборе констант r определить набор весов q=.
Итак, разработанный аппарат lk-представлений позволяет решать задачу сравнения и эффективного поиска в словаре не только отдельных именных компонент, но и многокомпонентных именных групп. Экспериментальные исследования и выбор параметров Как было показано выше, для гарантированного нахождения слова в словаре, содержащем слова различной длины, необходимо, чтобы используемый параметр нормализации l на единицу превышал длину самого длинного слова в словаре. С другой стороны, на практике для снижения объема индексного файла целесообразно ограничить значение l минимально возможным числом, определяющим так называемую значимую часть слова. При этом с уменьшением величины l объем индексного файла снижается, однако возрастает число ошибок первого рода. Для оценки минимально необходимого значения l на исследуемой базе ИГ была проведена серия вычислительных экспериментов, в которых исследовались распределение записей по количеству ИК в МИГ, распределение длин ИК, зависимость количества ошибок первого рода при различных l в условиях поиска с точностью до различных значений k. Экспериментально установлено, что значение l=7 является точкой насыщения в процессе уменьшения ошибок первого рода. В связи с этим значение l=7 было принято в качестве базового параметра при построении практических алгоритмов поиска ИГ. На рисунке 1 представлена эмпирическая функция распределения длин слов для ИГ в экспериментальных базах. Эмпирические зависимости количества ошибок первого рода (ложного отождествления слова с образцом) от длины нормализованного слова l и порогового значения коэффициента lk-корреляции K при k=1, 2 и 3 отражены на рисунках 2, 3, 4 соответственно. В заключение отметим, что в статье рассмотрена задача нечеткого поиска ИГ в специализированных базах персональных данных. Дана формальная постановка задачи, для решения которой предложен метод нечеткого сравнения и поиска слов с использованием lk-представлений, являющийся дальнейшим развитием подхода к поиску ИГ, описанного в [5]. Определены понятия lk-граммы, lk-представления слова Nlk(w) и словаря Nlk(U), lk-спектра слова по словарю, а также показателя и нормированного коэффициента lk-кореляции слов. Доказаны свойства нормированного коэффициента lk-кореляции. Получены аналитические зависимости пороговых значений показателя lk-кореляции от расстояния Левенштейна. Описан алгоритм нечеткого поиска ИГ с использованием lk-представлений, обеспечивающий гарантированное нахождение соответствий в базе для таких ИГ, степень искажения которых в метрике Левенштейна не превышает заданной. Данный алгоритм имеет сложность порядка O(||Nlk(w)||*ln(||Nlk(U)||)) операций, что существенно эффективнее алгоритмов прямого поиска в словаре. С целью определения оптимальных значений параметров алгоритма нечеткого поиска ИГ проведено экспериментальное исследование с использованием фрагментов реальных БД, содержащих ИГ. Экспериментально установлено, что значение l=7 является точкой насыщения в процессе уменьшения ошибок первого рода (ложных отождествлений ИГ). Литература 1. Бойцов Л.М. Классификация и экспериментальное исследование современных алгоритмов нечеткого словарного поиска // Электронные библиотеки: перспективные методы и технологии, электронные коллекции: RCDL2004: тр. 6-й Всеросс. науч. конф. URL: http://www.rcdl.ru/papers/2004/paper27. pdf (дата обращения: 10.01.10). 2. Левенштейн В.И. Двоичные коды с исправлением выпадений, вставок и замещений символов: докл. АН СССР. 1965. Т. 163. № 4. 3. Winkler W.E. Overview of Record Linkage and Current Research Directions // Research Report Series, 2006. 4. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1974. 222 с. 5. Бондаренко А.В., Герасименко А.А. Об одном алгоритме нечеткого поиска именных компонент в специализированных базах данных // Вестник компьютер. и информ. технол. 2005. № 8 (12). С. 29–34. |
| Permanent link: http://swsys.ru/index.php?id=2559&lang=en&page=article |
Print version Full issue in PDF (5.84Mb) Download the cover in PDF (1.43Мб) |
| The article was published in issue no. № 3, 2010 |
Back to the list of articles
 {Nlk(ui)}, где uiÎU; mU=||U||.
{Nlk(ui)}, где uiÎU; mU=||U||.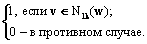
 clk(w,ui)´clk(v,ui),
clk(w,ui)´clk(v,ui), – биномиальный коэффициент. Соответственно,
– биномиальный коэффициент. Соответственно,
 =
= , откуда Kmin(l,k,x)=
, откуда Kmin(l,k,x)= .
. =
= =3/7.
=3/7. =2/7.
=2/7.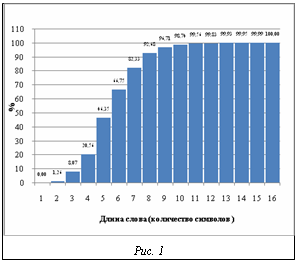 Рассмотрим задачу нечеткого отождествления ИГ, состоящих из нескольких именных компонент (ИК). Пусть даны две многокомпонентные ИГ (МИГ): словарная U== и тестовая (МИГ-запрос) W==.
Рассмотрим задачу нечеткого отождествления ИГ, состоящих из нескольких именных компонент (ИК). Пусть даны две многокомпонентные ИГ (МИГ): словарная U== и тестовая (МИГ-запрос) W==.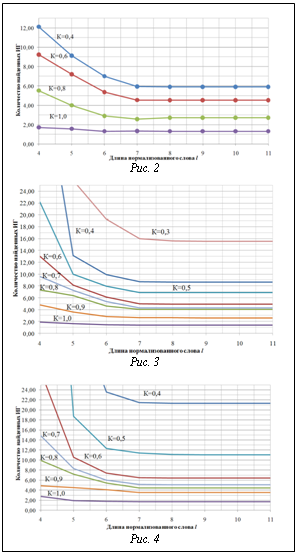 Легко заметить, что эта задача эквивалентна задаче представления числа rS в системе счисления с основаниями из r. К сожалению, такое разложение не будет единственным, поскольку система счисления r не является строго позиционной. Иными словами, сформулированная задача является некорректной. Однако, как известно из работ А.Н. Тихонова (например [4]), некорректные задачи становятся корректными, если удается их регуляризировать, то есть включить в нее некоторые дополнительные условия или критерии. Семантика рассматриваемой задачи позволяет естественным образом определить регуляризирующее условие, связанное с тем, что наличие ненулевых коэффициентов при малых t означает обнаружение в поисковом запросе неискаженных или слабо искаженных именных компонент, а вхождение ненулевых коэффициентов при больших t должно трактоваться как наличие большого количества отличающихся или сильно искаженных компонент. При этом информация о сильном совпадении небольшого количества ИК семантически более значима, чем информация о слабом совпадении большого количества ИК, так как на практике вероятность ошибок редактирования не столь велика. Это позволяет определить однозначную процедуру решения данной задачи, основанную на том, что в последовательности r каждый следующий элемент всегда меньше предыдущего ненулевого "t0)Þ(rt+10: pt=pt-1 mod rt-1, qt=pt div rt, t=1,…,l-1, где (a div b) –целочисленное деление a на b; (a mod b) – взятие остатка a по модулю b. После вычисления коэффициентов разложения критерий lkx-отождествимости МИГ вычисляется по приведенным выше формулам.
Легко заметить, что эта задача эквивалентна задаче представления числа rS в системе счисления с основаниями из r. К сожалению, такое разложение не будет единственным, поскольку система счисления r не является строго позиционной. Иными словами, сформулированная задача является некорректной. Однако, как известно из работ А.Н. Тихонова (например [4]), некорректные задачи становятся корректными, если удается их регуляризировать, то есть включить в нее некоторые дополнительные условия или критерии. Семантика рассматриваемой задачи позволяет естественным образом определить регуляризирующее условие, связанное с тем, что наличие ненулевых коэффициентов при малых t означает обнаружение в поисковом запросе неискаженных или слабо искаженных именных компонент, а вхождение ненулевых коэффициентов при больших t должно трактоваться как наличие большого количества отличающихся или сильно искаженных компонент. При этом информация о сильном совпадении небольшого количества ИК семантически более значима, чем информация о слабом совпадении большого количества ИК, так как на практике вероятность ошибок редактирования не столь велика. Это позволяет определить однозначную процедуру решения данной задачи, основанную на том, что в последовательности r каждый следующий элемент всегда меньше предыдущего ненулевого "t0)Þ(rt+10: pt=pt-1 mod rt-1, qt=pt div rt, t=1,…,l-1, где (a div b) –целочисленное деление a на b; (a mod b) – взятие остатка a по модулю b. После вычисления коэффициентов разложения критерий lkx-отождествимости МИГ вычисляется по приведенным выше формулам.