Software & Systems

Создание высокопроизводительных вычислительных систем всегда являлось стратегическим приоритетом лидирующих мировых держав и входит в первую десятку жизненно важных научно-технических программ. Без суперкомпьютеров невозможно обеспечить конкурентоспособность страны на мировом рынке, нельзя поддерживать обороноспособность государства на должном уровне. Неоценима роль высокопроизводительных вычислителей для бортовых систем, область применения которых обширна.

Успешное развитие многопроцессорных вычислительных систем обеспечивается в основном за счет роста технологических возможностей, в частности, за счет уменьшения топологических размеров при изготовлении кремниевых микросхем, вследствие чего повышается плотность компоновки вентилей на одном кристалле и возрастает скорость работы процессоров. Помимо технологических путей повышения производительности вычислительных систем, существуют алгоритмические, программные и архитектурные методы. Алгоритмические методы сводятся к построению более эффективных математических методов решения задач, программные состоят в разработке программ, обеспечивающих эффективное использование вычислительных систем. Важнейшим направлением повышения производительности вычислительных систем являются архитектурные методы.

Специалистами ведущих фирм мира за последние полвека были реализованы конвейерные, векторные, векторно-конвейерные, матричные, тороидальные, гиперкубовые, иерархические, кластерные и множество иных архитектур вычислительных систем. Лидирующие позиции в области высокопроизводительных систем занимают системы с кластерной архитектурой, представляющей собой объединение множества традиционных коммерчески доступных процессорных узлов с помощью стандартных сетевых решений. Однако данная архитектура имеет существенные недостатки, обусловленные относительно низкой скоростью процедур межпроцессорного обмена, недостаточной пропускной способностью сети передачи данных и необходимостью синхронизации множества взаимосвязанных последовательных процессов, каждый из которых выполняется на отдельном процессоре.

Все это приводит к тому, что высокую реальную производительность кластерная архитектура демонстрирует в основном только при решении слабосвязанных задач, не требующих интенсивного обмена данными между процессорными узлами, в то время как при решении сильносвязанных задач их реальная производительность не превышает 5–10 % от прогнозируемой. При этом увеличение числа процессорных узлов в системе зачастую не только не повышает ее реальную производительность, а наоборот, ведет к ее снижению, поскольку на организацию параллельного вычислительного процесса требуется больше времени, чем на его исполнение. Данное положение характерно для большинства существующих архитектур многопроцессорных вычислительных систем, то есть, если на некоторых классах задач при конкретной архитектуре достигается производительность, близкая к пиковой, то при решении других классов задач производительность той же вычислительной системы может резко падать, уменьшаясь на порядок или даже на несколько порядков.

Это обусловлено противоречием, вытекающим из неадекватности конкретной архитектуры многопроцессорной системы и внутренней структуры решаемой задачи. Снять его можно, разработав системы с реконфигурируемой архитектурой, изменяемой от задачи к задаче в отличие от многопроцессорных вычислительных систем с жесткой архитектурой. Таким образом, реализация концепции реконфигурируемых архитектур обеспечивает возможность адаптации архитектуры вычислительной системы под структуру решаемой проблемы, а также высокую реальную производительность многопроцессорной вычислительной системы, близкую к пиковой, на широком классе задач (в том числе при решении сильносвязанных задач) и практически линейный рост производительности при увеличении числа процессоров в системе [1].

Специалисты, использующие программируемые логические интегральные схемы (ПЛИС), считают, что применение данных кристаллов обеспечивает более чем на два порядка большую производительность систем в сравнении с реализованными на стандартных микропроцессорах системами с аналогичной потребляемой мощностью и стоимостью [2]. Особенно целесообразно применение данного подхода при создании встраиваемых бортовых вычислительных систем. Следует отметить, что концепция построения реконфигурируемых вычислительных структур открывает широкие перспективы использования ПЛИС в качестве элементной базы для создания больших вычислительных полей, в рамках которых могут создаваться проблемно-ориентирован­ные вычислительные системы, адаптируемые под структуру решаемой задачи.

Возможность создания таких систем обеспечит максимум эффективности при решении конкретной вычислительной задачи. Однако это только одна сторона медали. Другую формируют проблемы, связанные с привлечением высококвалифицированных специалистов, со специфичностью и сложностью программирования при разработке таких систем. Для реализации подобных систем необходимо программирование не только каждого отдельного процессорного элемента, но и структуры связей между ними в соответствии с информационным графом решаемой задачи.

Это требует больших временных затрат, применения нестандартных средств программирования, а также высокой квалификации программистов, разработчиков архитектурных решений. Именно этим объясняется то, что реконфигурируемые вычислительные системы до сих пор не нашли широкого применения. Их использование для решения часто меняющихся задач с одиночным вектором входных данных малоэффективно, но положение дел резко меняется для класса задач, при решении которых преимущества реконфигурируемых мультиконвейерных вычислительных систем проявляются в полной мере. Это задачи обработки больших массивов (потоков) данных по одному алгоритму.

Примерами могут служить задачи математической физики, цифровой обработки сигналов, криптографии и т.д.

Рассмотрим потоковую задачу, сформулированную следующим образом: существует некоторое упорядоченное множество векторов данных Vin=V1,V2,…Vn, каждый элемент которого должен быть обработан по фиксированному алгоритму A; задача потоковой обработки заключается в преобразовании множества (потока) векторов входных данных Vin во множество (поток) векторов выходных данных Vout. В простейшем случае решение подобных задач связано с применением последовательной вычислительной системы, основным элементом которой является процессор P. Для этого необходимо предварительно запрограммировать процессор на последовательное выполнение всех операций алгоритма и затем подать на вход последовательность векторов. Считая, что время обработки одного вектора на процессоре P равно PA, время, затраченное на последовательную обработку всего потока входных данных, равно n*PA. Самым очевидным путем сокращения времени обработки потока входных векторов является распараллеливание процесса обработки.

В простейшем случае параллельный способ подразумевает наличие нескольких процессоров (P1=P2=…=Pm=P), каждый из которых может работать независимо от других. В этом случае время решения, то есть время обработки всего множества векторов входных данных, будет равно (n/m)*PA, то есть сократится в m раз.

Сократить время решения можно и другим способом, который принято называть конвейерной обработкой. Предположим, что обработка каждого входного вектора проходит несколько стадий A=A1,A2…Am и в системе имеется несколько процессоров, соединенных последовательно, причем каждый из процессоров реализует определенную стадию общего алгоритма. Время обработки массива данных на конвейере процессоров будет зависеть от времени работы самой медленной ступени конвейера (обозначим ее PAi), тогда время обработки всего потока данных будет n*PAi.

Существенным преимуществом конвейерного способа обработки перед параллельным является сокращение числа входных и выходных информационных каналов. Рассмотренные способы оптимизации применимы для схемного представления вычислительной задачи. В рамках существующей парадигмы работы вычислительных систем на следующем шаге необходимо отобразить схемное представление вычислительной задачи в алгоритмическое. Для этого предлагается методика, позволяющая транслировать языки программирования высокого уровня в языки описания аппаратуры.

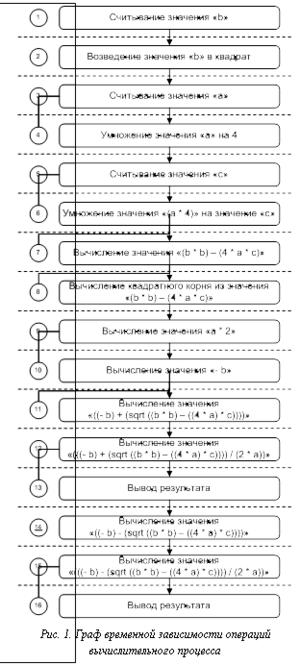Сущность ее заключается в устранении недостатка, связанного с применением графа специального вида. Так, исходный текст на языке программирования высокого уровня, реализующий алгоритм, принято неявно описывать графом вычислительного процесса, определяющим отношение временной зависимости операций алгоритма: Gw=, где O – множество операций нижнего уровня (они представляются операторами языка программирования); W – множество ребер, соответствующих последовательности выполнения операций; In – начальная операция; Out – множество всех возможных завершающих операций.

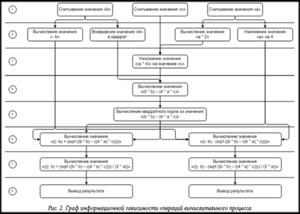
Недостаток подобного представления в том, что вычислительная система, построенная на основе такого графа, не может начать выполнение операции до тех пор, пока не закончится выполнение предыдущей, что соответствует последовательному выполнению алгоритма. Если определить на том же множестве O информационную зависимость операций, то можно получить представление процесса, отражающее граф информационной зависимости операций Gd. Такое представление вычислительного процесса определяет последовательность выполнения операций, зависящую от данных, необходимых для выполнения операции, и является исходным для построения схемного описания вычислительной системы для реконфигурируемой вычислительной системы. Построенный граф информационной зависимости процесса вычисления обладает двумя свойствами:

•    является максимально детальным для описания алгоритма на языке программирования высокого уровня, так как вершины представляют собой неделимые операции, предоставляемые языком программирования;

•    обеспечивает максимальную степень параллельного выполнения операций.

При описании построенного графа на языке описания аппаратуры вершины графа принимают вид аппаратных модулей, в которых определены входные и выходные шины данных, а ребра являются самими шинами данных, через которые проходит информация по вычислительной системе. Архитектура построенной по такому графу вычислительной системы полностью адекватна архитектуре процесса вычисления, что обеспечивает максимальную производительность реконфигурируемого вычислителя. Если полученное схемное решение требует большего количества аппаратных ресурсов, чем может предоставить созданный вычислитель, методика предусматривает оптимизацию схемного решения. На определенном шаге методики предполагается выполнение трех действий:

·     построение графа временной зависимости по алгоритмическому описанию вычислительного процесса;

·     построение графа информационной зависимости на основе графа временной зависимости;

·    

генерация схемного решения на основе графа информационной зависимости.

Граф временной зависимости строится по исходному коду на языке высокого уровня по следующей схеме: проводятся препроцессорная обработка, лексический, синтаксический и семантический анализы исходного текста, в результате чего строится дерево синтаксического разбора. Эти операции успешно осуществляются с помощью классического компилятора, описанного в [3] и имеющего модульную архитектуру, в которой каждая операция выполняется отдельным модулем. Модули препроцессора, лексического и синтаксического анализаторов зависят от исходного языка программирования.

При обработке добавляемого языка программирования эти модули должны быть написаны и заменять собой соответствующие модули. Модуль семантического анализа не зависит от исходного языка программирования и может использоваться для любого поддерживаемого языка программирования. Такая архитектура позволяет обрабатывать большой класс исходных языков программирования за счет взаимозаменяемости модулей, зависимых от исходного языка программирования. Стадии, зависимые от исходного языка программирования, абстрагируют исходный код до описания алгоритма (дерево синтаксического разбора), которое не зависит от исходного языка. Построение графа вычислительного процесса Gw по дереву синтаксического разбора реализуется рекурсивным обходом, при котором сначала выделяются операции, а затем определяются связи, отражающие передачу управления между операциями.

Детализацию методики осуществим на примере реализации алгоритма решения квадратного уравнения. На первом шаге описывается алгоритм на псевдоязыке.

Программа РешениеКвадратногоУравнения;

Начало

    { вводится значение параметра a }

    ПолучитьПараметр (a);

    { вводится значение параметра b }

    ПолучитьПараметр (b);

    { вводится значение параметра c }

    ПолучитьПараметр (c);

    { вычисляется дискриминант }

    Дискриминант = b*b-4*a*c;

    { вычисляется квадратный корень из дискриминанта }

    Переменная1 = КвадратныйКорень (Дискриминант);

    { вычисляется первый корень }

    Ответ1 = (-b - Переменная1)/(2*a);

    { Вывод первого корня }

    Вывести (Ответ1);

    { вычисляется второй корень }

    Ответ2 = (-b + Переменная1)/(2*a);

    { Вывод второго корня }

    Вывести (Ответ2);

Конец.

На втором шаге строится граф Gw (рис. 1), реализующий приведенный псевдокод.

Далее построенный граф процесса вычисления отражает последовательность выполнения действий алгоритма. У каждой операции есть входные и выходные данные, соответствующие передаче управления блоку и завершению его работы. Затем осуществляется переход от графа временной зависимости Gw к графу информационной зависимости Gd. При этом акцент смещается с потока управления на поток данных, что позволяет начать выполнение действия в любой момент после появления всех необходимых данных. Переход реализуется следующим алгоритмом: 1) определяются входные данные; 2) на первый слой графа помещаются операции, зависящие только от входных данных; 3) на каждый следующий слой помещаются операции, информационно зависящие от исходных данных и результов выполнения операций на предыдущих слоях.

Пример графа Gd, построенного по графу Gw, представлен на рисунке 2.

Полученный граф Gd подходит для генерации кода на языке описания аппаратуры в терминах аппаратных модулей, связывающихся друг с другом шинами данных, через которые происходит обмен информацией. То есть программирование аппаратного модуля является описанием графа Gd на языке описания аппаратуры. Код модулей, реализующих операции, пишется на языках описания аппаратуры и многократно используется для построения модулей более высокого уровня, соответствующих подграфам графа Gd.

Предложенный подход описывает преобразование алгоритмического представления вычислительной задачи в схемное. Применение этого подхода на практике позволит описывать вычислительный процесс на алгоритмических языках и преобразовывать его в схемное описание эквивалентного процесса, которое применяется в технологии создания программируемых реконфигурируемых бортовых высокопроизводительных вычислительных систем.

Литература

1.   Каляев А.В., Левин И.И. Модульно-наращиваемые многопроцессорные системы со структурно-процедурной организацией вычислений. М.: Янус-К, 2003. 380 с.

2.   Левин И.И. Методы и программно-аппаратные средства параллельных структурно-процедурных вычислений. Дисс. … докт. техн. наук. Таганрог, 2004. 363 с.

3.   Alfred V. Aho, Ravi Sethi, Jeffrey D. Ullman. Compilers Principles, Techniques, and Tools. 2006.