Journal influence
Bookmark
Next issue
Flying stock model by the linear programming method
The article was published in issue no. № 3, 2010Abstract:aircrafts, parametrical row, linear programming, simplex-method, economic effectiveness.
Аннотация:В статье обоснован и сформулирован метод определения потребного типа воздушного судна для конкретного маршрута из имеющегося множества при моделировании структуры парка воздушных судов. Метод основан на разработанном алгоритме с применением линейного программирования, а именно симплекс-метода.
| Authors: Pripadchev A.D. (aleksejj-pripadchev@rambler.ru) - Orenburg State University (Associate Professor), Orenburg, Russia, Ph.D | |
| Keywords: economical effectiveness, simplex-method, linear programming, parametrical row, aircrafts |
|
| Page views: 12615 |
Print version Full issue in PDF (5.84Mb) Download the cover in PDF (1.43Мб) |
В настоящее время авиапредприятия остро нуждаются в современных воздушных судах (ВС). Устаревший парк и новые требования к летно-техническим характеристикам являются основанием для моделирования структуры потребного парка ВС с использованием методов системного анализа и исследования операций [1]. Задача заключается в том, чтобы определить потребное количество ВС, обеспечивающих выполнение объемов пассажирских перевозок в установленные сроки, а также экономически выгодный тип ВС для каждого маршрута. Решение ее даст ответ на вопросы: какой тип ВС экономически эффективен на конкретном маршруте в процессе пассажирских перевозок (под ним понимается транспортировка пассажиров, выполняемая авиапредприятием на ВС за установленную плату в соответствии с условиями договора), а также сколько необходимо ВС для перевозки пассажиров на конкретном маршруте. Сущность и особенность предлагаемого метода определения структуры потребного парка ВС на основе критерия производственных расходов ВС заключаются в следующем. Методологическая и программная реализация модели – это определение потребной структуры парка ВС при перевозке из определенного пункта А пассажиров по n маршрутам. Целевой функцией является сумма производственных расходов на все рейсы для всех маршрутов при сохранении (увеличении) показателя дохода и при выполнении системы ограничений-равенств. Получаем задачу линейного программирования, которую решаем симплекс-методом. Переменными являются n – количество маршрутов и m – тип ВС. Ограничениями выступает система ограничений-равенств для всех маршрутов. Данная задача решается симплекс-методом, так как легко описывается линейной моделью и однозначно выполняется для минимизации целевой функции. Можно решить ее и стохастически, если имеются данные об изменении производственных расходов за неделю, месяц, квартал, год, однако эта информация является коммерческой тайной авиапредприятия. Решение задачи линейного программирования симплекс-методом носит итерационный характер. Для его методологического построения математическая модель структуры парка ВС представляется в стандартной форме линейных оптимизационных моделей, при этом все ограничения записываются в виде равенства с неотрицательной правой частью, значения всех переменных модели неотрицательны, целевая функция подлежит минимизации. В процессе построения математической модели необходимо четко представлять следующее: - для определения каких величин она строится; - какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделирующего процесса пассажирских перевозок; - в чем цель выбора из всех допустимых значений переменных тех, которые будут соответствовать оптимальному решению задачи. Трудность построения математической модели заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических функций этих переменных. Рассмотрим данный случай. Каждый маршрут обслуживают ВС всех типов, имеющихся в авиапредприятии. Для первого маршрута количество перевозимых пассажиров вычисляем по формуле
где аi,j – количество пассажиров, перевозимых за один рейс на i-м маршруте ВС j-го типа, Общую сумму расходов на все рейсы всех маршрутов вычисляем как
где сi,j – расходы на один рейс на i-м маршруте ВС j-го типа, i=1,2,…,n, j=1,2,…,m. Если необходимо минимизировать общую сумму расходов при выполнении системы ограничений-равенств, получим задачу линейного программирования, то есть этим методом находим Хi,j, где После определения Хi,j, при Если к системе ограничений-равенств добавить систему ограничений-равенств (неравенств) по количеству рейсов ВС каждого типа, получим общее количество рейсов на всех маршрутах для каждого типа ВС:
Добавляя к системе ограничений систему (3), можно минимизировать общую сумму расходов. В результате опять получим задачу линейного программирования, которую решаем симплекс-методом. Для решения необходимо задать bi, aij, cij, Kj, На основе метода линейного программирования разработано программное средство для оптимизации парка ВС [2], позволяющее определить экономически выгодное ВС на конкретном маршруте для конкретного авиапредприятия с имеющейся сетью маршрутов и с такими исходными данными, как тип ВС, количество пассажиров в ВС, количество перевезенных пассажиров в месяц, количество рейсов в месяц, крейсерская скорость, дальность полета, расход топлива, выручка в месяц. Кроме того, данное программное средство дает возможность найти гипотетический парк ВС авиапредприятия. Задавая в исходных данных современные типы ВС отечественного и иностранного производства, программа определяет экономически выгодное ВС с учетом вышеперечисленных исходных параметров. За руководителем (менеджером) авиапредприятия остается право выбора того или иного типа ВС. Поскольку модель содержит только две переменные, задачу можно решить графическим методом, заключающимся в геометрическом представлении допустимых решений, то есть построении области (допустимых) решений, в которой одновременно удовлетворяются все ограничения модели. В каждой точке, принадлежащей внутренней области, все ограничения выполняются, поэтому решение, соответствующее данным точкам, является допустимым. Пространство решений содержит бесконечное число таких точек, что не мешает найти потребное решение. После определения экономически выгодного ВС необходимо вычислить их потребное количество (nпотр) в парке авиапредприятия для осуществления пассажирских перевозок в полном объеме и в установленные сроки по формуле nпотр=Q/A, (4) где Q – количество перевезенных пассажиров в месяц; А – производительность ВС. Результат определения структуры потребного парка ВС для ФГУП «Оренбургские авиалинии» методом линейного программирования представлен в таблице.
На основании изложенного можно выделить следующие отличительные особенности рассмотренного метода, реализация которого предоставляет новые возможности при решении задач по управлению парком ВС авиапредприятий. Информация, полученная с помощью симплекс-метода, позволяет дать экономическую интерпретацию итогового решения. В результате решения уравнения (2) с системой ограничений при помощи программного средства выбран наилучший тип ВС из имеющегося парка ВС авиапредприятия на конкретном маршруте. Предлагаемый метод с программным средством для ЭВМ позволяет определить потребный парк ВС как по отдельным авиапредприятиям, так и по федеральным округам. Уравнение (4) дает возможность сформировать потребный парк ВС авиапредприятий из экономически эффективных типов ВС. В соответствии с таблицей по результатам применения метода линейного программирования потребный парк ВС для ФГУП «Оренбургские авиалинии» составляет 8 ВС типа Б737. Экономический эффект от внедрения метода – увеличение прибыли авиапредприятия в среднем в 1,7 раза за счет уменьшения количества ВС в парке и снижения расхода топлива. Результаты работы по определению потребной структуры парка ВС авиапредприятия отражены в научно-методических рекомендациях [3], утвержденных к применению Приволжским межрегиональным территориальным управлением воздушного транспорта, ФГУП «Оренбургские авиалинии», Минэкономразвития, промышленной политики и торговли Оренбургской области, ОАО «Авиакомпания «Уральские авиалинии», ОАО «ВПК «НПО машиностроения», КБ «Орион». За разработку и внедрение методологии оптимизации парка ВС на примере Оренбургской области ее авторы получили диплом лауреата премии губернатора Оренбургской области за достижения в сфере науки и техники за 2009 г. Литература 1. Припадчев А.Д., Султанов Н.З. Проблемы и перспективы развития рынка гражданской авиации Российской Федерации // Интеллект. Инновации. Инвестиции. 2009. № 1. С. 27–31. 2. Припадчев А.Д., Султанов Н.З., Чеховский А.В. Программа для оптимизации парка воздушных судов. Свид. о гос. регистр. прогр. для ЭВМ № 2010611242. Зарегистр. в Реестре программ для ЭВМ 12 февраля 2010 г. М.: Федеральная служба по интеллектуальной собственности, патентам и товарным знакам, 2010. 3. Припадчев А.Д., Султанов Н.З. Оптимизация парка воздушных судов авиапредприятий: науч.-методич. рекоменд. Оренбург: ОГУ, 2010. | ||||||||||||||||||||||||||||||||||||
| Permanent link: http://swsys.ru/index.php?id=2570&lang=en&page=article |
Print version Full issue in PDF (5.84Mb) Download the cover in PDF (1.43Мб) |
| The article was published in issue no. № 3, 2010 |
Perhaps, you might be interested in the following articles of similar topics:
- Применение метода линейного программирования при автоматизированном проектировании дополнительных аэродинамических поверхностей
- Построение и оптимизация производственной программы разделительного комплекса
- Методика оценки эффективности мероприятий по развитию технологии открытых систем
- Программная реализация метода автоматизированного проектирования фюзеляжа воздушного судна с помощью объектно-ориентированных технологий
- Моделирование вихревых следов в задачах управления воздушным движением
Back to the list of articles
 . (1)
. (1) ,
,  ; bi – количество авиапассажиров, перевозимых по i-му маршруту,
; bi – количество авиапассажиров, перевозимых по i-му маршруту,  , (2)
, (2)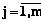 .
. . (3)
. (3)