Создание современных программных средств, обеспечивающих качественную обработку дихотомических результатов тестирования, анализ полученных данных и их интерпретацию, связано с разработкой теоретических основ и алгоритма расчета латентных параметров участников тестирования θ и дихотомических заданий (индикаторов) диагностического теста β. Для решения подобной задачи могут использоваться различные математические методы, которые нашли применение в теории педагогических измерений. Это методы PROX, попарного сравнения [1], моментов, максимального правдоподобия [2] и др. При выборе конкретного метода необходимо учитывать, что расчет латентных параметров зачастую выполняется по нормативным выборкам небольшого объема, поэтому полученные оценки параметров θ* и β* могут отличаться от объективно существующих точных значений θ и β. В связи с этим возникает необходимость в исследовании несмещенности, эффективности и состоятельности оценок θ* и β*. Избежать проведения подобных исследований можно, если теоретическое обоснование алгоритма вычисления латентных параметров провести методом максимального правдоподобия. Этот метод наиболее полно использует данные выборки для расчета параметра, и получаемые с его помощью оценки являются состоятельными, асимптотически несмещенными и асимптотически эффективными [2]. Это обстоятельство позволило выбрать метод максимального правдоподобия для разработки теоретических основ расчета латентных параметров θ и β – уровня подготовленности участника тестирования и уровня трудности индикатора диагностического теста соответственно.
В качестве модели измерения, с использованием которой вычисляются латентные параметры, используется однопараметрическая модель Г. Раша [2, 3]. Некоторые математики-теоретики считают, что эта модель получена и обоснована им экспериментально и не имеет убедительного теоретического обоснования. Поэтому разработку математического аппарата, необходимого для расчета параметров латентных переменных, следует начать с теоретического обоснования допустимости использования однопараметрической модели Раша для оценки результатов образовательной деятельности.
Перед датским математиком Г. Рашем была поставлена задача: исследовать, как в процессе обучения изменяются навыки чтения школьниками незнакомого текста. Исследования должны были выполняться при соблюдении следующих требований:
– соответствие текстов уровню подготовленности школьника: не слишком трудные или слишком легкие;
– использование различных текстов при каждом исследовании;
– измерение значений уровня подготовленности школьников по одной и той же шкале.
При решении поставленной задачи для статистики выбиралось число ошибок, допущенных при чтении. На основе обработки и анализа многочисленных данных и диаграмм Г. Раш предположил в качестве гипотезы, что среднее число ошибок  , сделанных p-м школьником с уровнем подготовленности Dp при чтении t-го текста с трудностью Bt, можно представить в виде
, сделанных p-м школьником с уровнем подготовленности Dp при чтении t-го текста с трудностью Bt, можно представить в виде  .
.
Тогда отношение среднего числа ошибок  и
и  , которые допустит p-й школьник при чтении двух текстов разной трудности B1 и B2, определится только отношением этих трудностей и не будет зависеть от уровня подготовленности школьника:
, которые допустит p-й школьник при чтении двух текстов разной трудности B1 и B2, определится только отношением этих трудностей и не будет зависеть от уровня подготовленности школьника:
 .
.
Исходя из полученного результата Г. Раш пришел к выводу о том, что трудность всех текстов, которые используются для проверки уровня подготовленности школьников в чтении, можно откалибровать относительно некоторого стандартного текста и представить на одной шкале. Школьникам можно дать для проверки навыков чтения любой из текстов, и их уровень подготовки будет измерен по одной и той же шкале.
Один из важнейших выводов, сделанных Рашем в результате обработки и анализа результатов исследования, заключался в том, что для оценки навыков чтения школьником незнакомого текста необходимо использовать вероятностный подход. Это в наибольшей степени соответствует результатам прочтения текста. Например, хорошо подготовленный школьник может допустить много ошибок при прочтении легкого текста, а плохо подготовленный – прочесть трудный текст с малым количеством ошибок. Никогда нельзя точно предсказать, прочтет или не прочтет безошибочно школьник незнакомый текст, но можно сказать, насколько у него высоки шансы сделать это.
Для расчета вероятности Pnj правильного прочтения j-го текста трудностью βj школьником n с уровнем подготовленности θi Рашем была предложена однопараметрическая дихотомическая модель  , (1)
, (1)
которая в дальнейшем нашла широкое применение в оценке результатов образования, для социологических и психодиагностических исследований и в других областях.
Рассмотрим обоснование допустимости использования дихотомической модели Раша для оценки результатов образовательной деятельности с учетом изложенных ранее требований. Пусть n-й студент выполняет тест по учебной дисциплине, состоящий из j заданий (j=1, 2, …, L). Результат выполнения каждого задания обозначим через xnj. Величина xnj может принимать два значения:

Индивидуальный балл n-го студента (общее число успешно выполненных заданий)  позволяет получить представление об уровне знаний материала дисциплины, но на его основании нельзя прогнозировать выполнение других заданий. Для получения прогноза безусловно необходимой информацией является знание того, с какой вероятностью в следующий раз n-й студент успешно выполнит j-е задание теста. Иначе говоря, при оценке уровня подготовленности студента, как и при оценке навыков чтения незнакомого текста школьником, необходимо использовать вероятностную модель. Никогда нельзя точно предсказать, решит или не решит студент задачу, но можно сказать, каковы его шансы решить ее.
позволяет получить представление об уровне знаний материала дисциплины, но на его основании нельзя прогнозировать выполнение других заданий. Для получения прогноза безусловно необходимой информацией является знание того, с какой вероятностью в следующий раз n-й студент успешно выполнит j-е задание теста. Иначе говоря, при оценке уровня подготовленности студента, как и при оценке навыков чтения незнакомого текста школьником, необходимо использовать вероятностную модель. Никогда нельзя точно предсказать, решит или не решит студент задачу, но можно сказать, каковы его шансы решить ее.
Рассмотрим прогноз выполнения задания теста студентами m и n. Обозначим через Pnj вероятность того, что n-й студент успешно выполнит j-е задание теста. Тогда величина (1-Pnj) будет равна вероятности того, что этот студент неверно выполнит то же задание. Аналогичные обозначения введем для m-го студента. В соответствии с теоремой об умножении вероятностей матрица ожидаемых результатов для этих студентов может быть представлена в виде таблицы.
Возможные исходы выполнения задания студентами
|
Студент m
|
Студент n
|
|
Задание выполнено, xnj=1
|
Задание не выполнено, xnj=0
|
|
Задание выполнено, xmj=1
|
PmjPnj
|
Pmj(1–Pnj)
|
|
Задание не выполнено, xmj=0
|
(1–Pmj)Pnj
|
(1–Pmj)(1–Pnj)
|
Пусть два студента выполняют один и тот же набор тестовых заданий, одинаковых по трудности с заданием j и проверяющих один и тот же элемент содержания учебной дисциплины. Обозначим через N11 число заданий, успешно выполненных обоими студентами; N10 – число заданий, успешно выполненных только m-м студентом; N01 – число заданий, успешно выполненных только студентом n; N00 – число заданий, не выполненных обоими студентами.
При сравнении достижений студентов информативными являются только числа N10 и N01, которые соответствуют успешному выполнению заданий одним из студентов. Числа N11 и N00 не дают информации о том, у какого студента уровень подготовленности выше. Из таблицы видно, что число заданий N10, успешно выполненных только студентом m, будет прямо пропорционально произведению вероятностей Pmj(1–Pnj). Аналогично число заданий N01, успешно выполненных только студентом n, будет прямо пропорционально произведению вероятностей (1–Pmj)Pnj. Отношение числа N10 к числу N01 определяется выражением
 ~
~ . (2)
. (2)
При бесконечно большом числе заданий L (L→∞) оно определяет соотношение уровней подготовленности студентов m и n. Логично предположить, что выражение (2) не должно зависеть от трудности заданий в наборе. Поэтому для другого набора множества заданий, одинаковых по трудности с другим заданием k теста и проверяющих один и тот же элемент содержания учебной дисциплины, получится аналогичное выражение. Причем соотношение уровней подготовленности студентов должно остаться прежним. Поэтому для наборов заданий k и j можно записать
 . (3)
. (3)
Из выражения (3) следует, что
 (4)
(4)
Для обеспечения объективности сравнения необходимо, чтобы соотношение между любой парой наборов заданий j и k было справедливо для любого студента m. Поэтому уровень подготовленности некоторого студента с индексом 0 и любого набора заданий одинаковой трудности с индексом 0 могут быть условно приняты в качестве точек отсчета при проведении этих сравнений. Для получения единой шкалы сравнения подготовленности студентов и трудности заданий удобно выбрать одну точку отсчета, считая подготовленность студента и трудность набора заданий с индексами 0 эквивалентными, так что P00 будет равно 0,5. Заменяя в выражении (4) индексы m и k на 0, получим
 (5)
(5)
Первый сомножитель полученного выражения  представляет собой уровень подготовленности n-го студента в выбранной системе отсчета и является только его свойством. Второй сомножитель –
представляет собой уровень подготовленности n-го студента в выбранной системе отсчета и является только его свойством. Второй сомножитель –  – это величина, обратная трудности j-го задания в той же системе отсчета, которая является исключительно свойством этого задания.
– это величина, обратная трудности j-го задания в той же системе отсчета, которая является исключительно свойством этого задания.
С учетом введенных обозначений выражение (5) запишется в виде
 . (6)
. (6)
Таким образом, шанс n-го студента успешно выполнить j-е задание теста определяется отношением его уровня подготовленности к уровню трудности задания.
Прологарифмировав обе части уравнения (6), найдем

Обозначая  , а
, а  , получим:
, получим: 
 или
или  .
.
Решая данное уравнение, найдем вероятность Pnj успешного выполнения j-го задания n-м студентом:
 . (7)
. (7)
Выражение (7) представляет собой вероятность выполнения студентом n задания j, если известны его уровень подготовленности θn и уровень трудности задания βj, выраженные в логитах. Оно совпадает с формулой (1), полученной Рашем. При расчете θn и βj количественно измеряются уровень подготовленности n-го студента и уровень трудности j-го задания соответственно.
Теоретические основы расчета латентных переменных по дихотомическим данным
Параметры латентных переменных – уровня подготовленности студента θn и уровня трудности заданий βj – рассчитываются по результатам тестирования, которые представляются в виде матрицы ответов. Каждая строка такой матрицы – это профиль ответов студента на L заданий теста, а каждый столбец – профиль ответов всех N студентов на одно конкретное задание. Элемент матрицы ответов xnj отражает результат выполнения n-м участником тестирования j-го задания и может принимать значения 1 или 0.
Вероятностная модель значений xnj описывается однопараметрической моделью Раша, которая определяется формулой
 . (8)
. (8)
Найдем выражения для расчета параметров θn и βj, используя для этого решение задачи максимального правдоподобия для матрицы ответов размером N´L в предположении независимости величин Xi, Yj, θn и βj (N – количество участников тестирования, L – количество заданий в тесте). Вероятность правильного ответа всех N участников тестирования на все L заданий теста, представляющая собой функцию максимального правдоподобия Λ, определится произведением вероятностей  , рассчитанных по формуле (8):
, рассчитанных по формуле (8):
 .(9)
.(9)
Логарифмируя левую и правую части выражения (9), получим
 (10)
(10)
где  – первичный балл n-го участника тестирования, равный общему количеству полученных им баллов;
– первичный балл n-го участника тестирования, равный общему количеству полученных им баллов;  – первичный балл j-го задания, равный числу участников тестирования, успешно выполнивших его.
– первичный балл j-го задания, равный числу участников тестирования, успешно выполнивших его.
Для получения выражений, которые позволяют рассчитать значения уровня подготовленности θn n-го участника тестирования и уровня трудности βj j-го задания, найдем максимальное значение логарифмической вероятности l, продифференцировав выражение (10) по латентным переменным θn и βj и приравняв производные к нулю:
 (11)
(11)
Для решения системы уравнений (11) воспользуемся предложенным Ньютоном методом численного решения нелинейного уравнения вида f(x)=0.
Если функция f(x) дважды дифференцируема в окрестности точки x0, значение аргумента x(t+1) на (t+1) шаге итерации может быть вычислено на основе выражения
 . (12)
. (12)
Примем  в качестве функции f(θn), а
в качестве функции f(θn), а  – как функцию f(βj). Для определения производных f ¢(θn) и f ¢(βj) необходимо вычислить вторые производные
– как функцию f(βj). Для определения производных f ¢(θn) и f ¢(βj) необходимо вычислить вторые производные  и
и  от логарифмической функции максимального правдоподобия l. Найдем их. Вторая частная производная от левой части первого уравнения (11) запишется в виде
от логарифмической функции максимального правдоподобия l. Найдем их. Вторая частная производная от левой части первого уравнения (11) запишется в виде
 (13)
(13)
Аналогичным образом найдем вторую частную производную от второго уравнения системы (11):
 . (14)
. (14)
Подставляя f(θn), f(βj), f ¢(θn) и f ¢(βj) из выражений (11), (13), (14) в формулу (12), получим рекуррентные соотношения для расчета значений θn и βj:
 (15)
(15)
 (16)
(16)
 Итерационный процесс вычисления латентных переменных θn и βj завершается при выполнении условия s£D/3, где Δ – заданная погрешность вычислений; σ – значение среднеквадратичного отклонения очередного приближения t-й итерации от аналогичных оценок, полученных на предыдущей итерации (t–1) [2]:
Итерационный процесс вычисления латентных переменных θn и βj завершается при выполнении условия s£D/3, где Δ – заданная погрешность вычислений; σ – значение среднеквадратичного отклонения очередного приближения t-й итерации от аналогичных оценок, полученных на предыдущей итерации (t–1) [2]:
 . (17)
. (17)
Стандартные погрешности расчета e(θn) и e(βj) величин θn и βj определяются знаменателями формул (16) для последней итерации:
 ;
;
 . (18)
. (18)
Алгоритм расчета латентных переменных по дихотомическим данным
На основе полученных выражений определим последовательность выполнения операций для нахождения θn, βj. Алгоритм расчета представляет собой следующую последовательность действий (см. рис.).
1. Определить начальные значения параметров  и
и  на основе выражений
на основе выражений
 ,
,
где Pn=Xn/L – доля баллов, полученных n-м участником тестирования при выполнении L заданий теста;
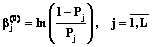 ,
,
где Pj=Yj/N – доля баллов, полученных N участниками тестирования при выполнении j-го задания теста. Если Pn=1, Pj=1 или Pn=0, Pj=0, то профиль ответов n-го участника тестирования или j-го задания из обработки исключается.
2. Используя начальные значения  , вычислить уточненные значения
, вычислить уточненные значения  при t=0 по формуле (15). Итерационные вычисления повторяются до тех пор, пока выполняется условие
при t=0 по формуле (15). Итерационные вычисления повторяются до тех пор, пока выполняется условие
 .
.
3. Используя начальные значения  , найти
, найти  при t=0 по формуле (16). Значения
при t=0 по формуле (16). Значения  после каждой итерации центрируют:
после каждой итерации центрируют:

Итерационные вычисления продолжить до тех пор, пока выполняется условие  .
.
4. Вычислить значение критерия завершения итерационного вычисления латентных переменных θn и βj, используя выражение (17).
5. Если d£D/3, завершить итерационные вычисления (Δ=min(Δθ, Δβ)). В противном случае повторить шаги алгоритма со 2-го по 5-й, используя вместо  и
и  полученные значения
полученные значения  и
и  .
.
6. По формулам (18) вычислить погрешности расчетов для последней итерации.
Рассмотренный алгоритм расчета параметров латентных переменных по дихотомической матрице результатов тестирования используется в программном комплексе RILP-1M [4]. Достоверность полученных с его помощью значений параметров подтверждается высокой сходимостью расчетных данных к эмпирическим, согласием их с оценками, рассчитанными с помощью лицензионной диалоговой системы RUMM 2020.
Литература
1. Wright B.S., Masters G.N. Rating Scale Analysis: Rasch Measurement, Chicago, MESA Press, 1982. 206 p.
2. Нейман Ю.М., Хлебников В.А. Введение в теорию моделирования и параметризации педагогических тестов. М.: Прометей, 2000. 169 с.
3. Rasch G. Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen, Denmark: Danish Institute for Educational Research, 1960. 160 p.
4. Елисеев И.Н., Елисеев И.И., Фисунов А.В. Програм- мный комплекс RILP-1 // Программные продукты и системы. 2009. № 2. С. 178–181.
 , сделанных p-м школьником с уровнем подготовленности Dp при чтении t-го текста с трудностью Bt, можно представить в виде
, сделанных p-м школьником с уровнем подготовленности Dp при чтении t-го текста с трудностью Bt, можно представить в виде  .
. и
и  , которые допустит p-й школьник при чтении двух текстов разной трудности B1 и B2, определится только отношением этих трудностей и не будет зависеть от уровня подготовленности школьника:
, которые допустит p-й школьник при чтении двух текстов разной трудности B1 и B2, определится только отношением этих трудностей и не будет зависеть от уровня подготовленности школьника: .
. , (1)
, (1)
 позволяет получить представление об уровне знаний материала дисциплины, но на его основании нельзя прогнозировать выполнение других заданий. Для получения прогноза безусловно необходимой информацией является знание того, с какой вероятностью в следующий раз n-й студент успешно выполнит j-е задание теста. Иначе говоря, при оценке уровня подготовленности студента, как и при оценке навыков чтения незнакомого текста школьником, необходимо использовать вероятностную модель. Никогда нельзя точно предсказать, решит или не решит студент задачу, но можно сказать, каковы его шансы решить ее.
позволяет получить представление об уровне знаний материала дисциплины, но на его основании нельзя прогнозировать выполнение других заданий. Для получения прогноза безусловно необходимой информацией является знание того, с какой вероятностью в следующий раз n-й студент успешно выполнит j-е задание теста. Иначе говоря, при оценке уровня подготовленности студента, как и при оценке навыков чтения незнакомого текста школьником, необходимо использовать вероятностную модель. Никогда нельзя точно предсказать, решит или не решит студент задачу, но можно сказать, каковы его шансы решить ее. ~
~ . (2)
. (2) . (3)
. (3) (4)
(4) (5)
(5) представляет собой уровень подготовленности n-го студента в выбранной системе отсчета и является только его свойством. Второй сомножитель –
представляет собой уровень подготовленности n-го студента в выбранной системе отсчета и является только его свойством. Второй сомножитель –  – это величина, обратная трудности j-го задания в той же системе отсчета, которая является исключительно свойством этого задания.
– это величина, обратная трудности j-го задания в той же системе отсчета, которая является исключительно свойством этого задания. . (6)
. (6)
 , а
, а  , получим:
, получим: 
 или
или  .
. . (7)
. (7) . (8)
. (8) , рассчитанных по формуле (8):
, рассчитанных по формуле (8): .(9)
.(9) (10)
(10) – первичный балл n-го участника тестирования, равный общему количеству полученных им баллов;
– первичный балл n-го участника тестирования, равный общему количеству полученных им баллов;  – первичный балл j-го задания, равный числу участников тестирования, успешно выполнивших его.
– первичный балл j-го задания, равный числу участников тестирования, успешно выполнивших его. (11)
(11) . (12)
. (12) в качестве функции f(θn), а
в качестве функции f(θn), а  – как функцию f(βj). Для определения производных f ¢(θn) и f ¢(βj) необходимо вычислить вторые производные
– как функцию f(βj). Для определения производных f ¢(θn) и f ¢(βj) необходимо вычислить вторые производные  и
и  от логарифмической функции максимального правдоподобия l. Найдем их. Вторая частная производная от левой части первого уравнения (11) запишется в виде
от логарифмической функции максимального правдоподобия l. Найдем их. Вторая частная производная от левой части первого уравнения (11) запишется в виде (13)
(13) . (14)
. (14) (15)
(15) (16)
(16)
 . (17)
. (17) ;
; . (18)
. (18) и
и  на основе выражений
на основе выражений ,
,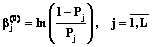 ,
, , вычислить уточненные значения
, вычислить уточненные значения  при t=0 по формуле (15). Итерационные вычисления повторяются до тех пор, пока выполняется условие
при t=0 по формуле (15). Итерационные вычисления повторяются до тех пор, пока выполняется условие .
. , найти
, найти  при t=0 по формуле (16). Значения
при t=0 по формуле (16). Значения  после каждой итерации центрируют:
после каждой итерации центрируют:
 .
. и
и  .
.