Устранение глобальной продовольственной проблемы является одной из основных задач Программы развития ООН, направленной на уменьшение до 2015 года числа людей, страдающих от недоедания [1]. В условиях ограниченности природных ресурсов и наблюдаемого демографического роста использование парников становится одним из альтернативных решений проблемы продовольственной безопасности и эффективного использования природных ресурсов, так как выращивание сельскохозяйственных культур в парниковых условиях в 10 раз эффективнее, чем в открытом грунте [2].
В решении оптимизационных задач накоплен достаточно большой опыт, который в основном касается исследований, связанных с построением детерминированных моделей математического программирования. Применительно к задачам оптимального распределения традиционные модели не учитывают того, что наблюдение за входными величинами и определение имеющихся ограничений по существу проводятся на уровне мягких измерений или в лучшем случае интервально. В то же время использование усредненных данных в моделях, характеризующихся большим числом входных величин и параметров, в конечном итоге приводит к получению неадекватных решений. Поэтому для решения задачи эффективного распределения парниковых площадей между сельскохозяйственными культурами предлагается исходить из категории полезности, которая по своей сути является одной из важных и трудноформализуемых характеристик производственного (в данном случае сельскохозяйственного) поведения.
При исследовании полезности необходимо иметь в виду, что, во-первых, производители сельскохозяйственных культур обладают всей полнотой информации, относящейся к их производственным решениям (о выращиваемых культурах и способности каждой из них обеспечить необходимую полезность, о ценах на эти культуры, а также о собственных доходах), и, во-вторых, они способны ранжировать все мыслимые распределения посевов на основе возможности каждого обеспечить полезность. Сельхозпроизводитель всегда пытается максимизировать свой уровень удовлетворенности, или, как его называют экономисты, полезность, которая определяется как индивидуальное восприятие удовлетворенности от производимого набора выращиваемых парниковых культур.
С математической точки зрения поведение производителя выражается в выборе некоторой точки из пространства выращиваемых культур. Если предположить наличие n парниковых культур, то суммарное количество по каждой из них характеризуется набором X=(x1, x2, …, xn), где xi обозначает количество выращенной i-й тепличной культуры. Все культуры обладают свойством произвольной делимости, то есть может быть выращено любое неотрицательное количество каждой из них. Поэтому все возможные наборы образуют замкнутое выпуклое векторное пространство
C={X=(x1, x2, …, xn)ïxi³0, i=1÷n}, (1)
являющееся слабо упорядоченным и непрерывным [3]. Последнее позволяет утверждать, что на этом пространстве наборов существует непрерывная действительная функция U(·), называемая функцией полезности, для которой при предпочтительности набора X над Y имеет место неравенство U(X)≥U(Y). Если U является некоторым индексом полезности, значение этого индекса зависит от производимых количеств парниковых культур xi.
Формализовать функцию полезности достаточно сложно. Существует несколько ее аналитических интерпретаций [3], однако ни одна из них не может считаться универсальной. Поэтому в настоящей работе предлагается нейронечеткий подход к построению функции полезности в предметной области, основанный на применении метода, описанного в [4]. Отправным моментом здесь является то, что основные экзогенные величины (посевные площади и рыночные цены на тепличные культуры) описываются интервально, а значения соответствующей им функции полезности и вовсе имеют условную природу. Для выборочных распределительных наборов, удовлетворяющих заданным ограничениям на посевные площади и рыночные цены, вычисляются соответствующие значения функции полезности. Далее на базе полученной выборки (набор – полезность) и feedforward нейронной сети с одним скрытым слоем идентифицируется сама функция полезности.
 Сформулируем задачу. Пусть для выращивания тепличных культур пространством всевозможных распределительных наборов будет замкнутое и выпуклое векторное гиперпространст- во (1). В условиях ограниченности площади тепличного хозяйства и рыночных цен на парниковые культуры необходимо построить соответствующую функцию полезности от распределительного набора и идентифицировать ее параметры.
Сформулируем задачу. Пусть для выращивания тепличных культур пространством всевозможных распределительных наборов будет замкнутое и выпуклое векторное гиперпространст- во (1). В условиях ограниченности площади тепличного хозяйства и рыночных цен на парниковые культуры необходимо построить соответствующую функцию полезности от распределительного набора и идентифицировать ее параметры.
Для оптимального распределения посевных площадей между тепличными культурами производитель может пользоваться так называемой картой кривых безразличия, каждая из которых в классической интерпретации представляет собой геометрическое место точек (распределительных наборов) в пространстве, размерность которого определяется числом выращиваемых культур. Очевидно, что в силу ограниченности посевных площадей среди этих кривых безразличия только одна кривая располагает точкой, в которой достигается максимальная полезность от использования соответствующего распределительного набора посевных площадей. В многомерном случае это точка касания соответствующей кривой безразличия с гиперплоскостью прибыли производителя в пространстве цен на культуры.
Пусть xi – количество выращенной i-й сельскохозяйственной культуры, Pi – рыночная цена на одну единицу (тонну) i-й культуры, B – общая прибыль фермера. Тогда для конкретного уровня прибыли от реализации тепличных культур оптимальный распределительный набор можно выявить на основе модели
P1x1+P2x2+…+Pnxn=B, (2)
U(x1, x2, …, xn)®max, (3)
где U(×): Ân®Â – функция полезности от набора (x1, x2, …, xn).
Специалисты в области эконометрики вполне резонно могут возразить такой постановке задачи, так как обычно в качестве целевой функции принято выбирать функцию прибыли (2), а саму задачу линейного программирования для данного случая описывать, например, как

где si – площадь, отводимая для выращивания i-й тепличной культуры; ei – ее урожайность. Однако допустим, что фермер взял у государства кредит и ему заранее необходимо знать, сколько посевной площади для выращивания тепличных культур потребуется и как ее оптимально распределить между культурами, чтобы своевременно возместить кредит, покрыть другие расходы и получить необходимый остаток для дальнейшего развития. Поэтому считаем, что постановка задачи в редакции (2)–(3) наиболее полно отражает существо проблемы, так как с ее помощью можно установить подходящие наборы (x1, x2 ,…, xn) для различных уровней кривых безразличия (рис. 1), описывающих объемы прибыли или предполагаемых кредитов (в каждой точке кривой безразличия функция полезности имеет одни и те же значения).
 Для определения полезности в каждом конкретном случае необходимо иметь в виду, что в условиях динамично развивающегося продовольственного рынка и конкурентной среды цены на парниковые культуры и доходы от их реализации не могут оставаться строго фиксированными. Как правило, они варьируются в определенных пределах и в краткосрочном периоде характеризуются усредненными значениями. В конечном итоге это приводит к погрешностям, которые не позволяют получить адекватные решения. Поэтому для описания рыночных цен на тепличные культуры и прибыли производителей в модели (2)–(3) целесообразно использовать лингвистические переменные со значениями в виде нечетких терм-множеств. Более того, само понятие «полезность» является скорее качественной категорией, нежели количественной, и поэтому как критерий полезности можно также использовать лингвистическую переменную, принимающую нечеткие значения. В результате модель (4)–(5) можно заменить ее нечетким аналогом:
Для определения полезности в каждом конкретном случае необходимо иметь в виду, что в условиях динамично развивающегося продовольственного рынка и конкурентной среды цены на парниковые культуры и доходы от их реализации не могут оставаться строго фиксированными. Как правило, они варьируются в определенных пределах и в краткосрочном периоде характеризуются усредненными значениями. В конечном итоге это приводит к погрешностям, которые не позволяют получить адекватные решения. Поэтому для описания рыночных цен на тепличные культуры и прибыли производителей в модели (2)–(3) целесообразно использовать лингвистические переменные со значениями в виде нечетких терм-множеств. Более того, само понятие «полезность» является скорее качественной категорией, нежели количественной, и поэтому как критерий полезности можно также использовать лингвистическую переменную, принимающую нечеткие значения. В результате модель (4)–(5) можно заменить ее нечетким аналогом:
 , (4)
, (4)
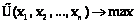 , (5)
, (5)
где  – нечеткая рыночная цена i-й тепличной культуры;
– нечеткая рыночная цена i-й тепличной культуры; 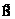 – нечеткая прибыль производителя. Функциональную зависимость в модели (4)–(5), заданную в неявном виде, определим путем построения нечетких правил, где лингвистическую переменную «полезность» будем считать эндогенной величиной, а «прибыль производителя» и «рыночные цены» на тепличные культуры рассматривать как экзогенные лингвистические переменные. В конечном итоге задачей является построение семейства нечетких уровней полезности от реализуемых распределительных наборов парниковых культур, дефаззифицированные значения которых и будут значениями искомой функции полезности.
– нечеткая прибыль производителя. Функциональную зависимость в модели (4)–(5), заданную в неявном виде, определим путем построения нечетких правил, где лингвистическую переменную «полезность» будем считать эндогенной величиной, а «прибыль производителя» и «рыночные цены» на тепличные культуры рассматривать как экзогенные лингвистические переменные. В конечном итоге задачей является построение семейства нечетких уровней полезности от реализуемых распределительных наборов парниковых культур, дефаззифицированные значения которых и будут значениями искомой функции полезности.
Предположим, что для ожидаемой прибыли заранее необходимо выявить оптимальное распределение посевных парниковых площадей между культурами, то есть для каждого уровня прибыли Bk (k=1÷q) необходимо подобрать оптимальный набор 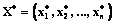 . Тогда функциональную зависимость в модели (4)–(5) представим в виде достаточного набора нечетких правил вида
. Тогда функциональную зависимость в модели (4)–(5) представим в виде достаточного набора нечетких правил вида
если 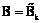 и
и 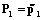 и
и 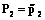
и … и  , то
, то 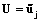 , (6)
, (6)
где  (k=1÷q) – нечеткий k-й уровень прибыли производителя;
(k=1÷q) – нечеткий k-й уровень прибыли производителя; 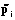 (i=1÷n) – нечеткий уровень цены на i-ю культуру;
(i=1÷n) – нечеткий уровень цены на i-ю культуру; 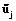 – j-е нечеткое значение критерия полезности U.
– j-е нечеткое значение критерия полезности U.
Для реализации предлагаемого подхода воспользуемся текущими данными о выращивании и реализации парниковых культур в Исламской Республике Иран. В качестве примера выбраны сельскохозяйственные культуры, востребованные на продовольственном рынке Ирана (табл. 1).
Таблица 1
|
Условное обозначение
|
Культура
|
Урожайность (т/га)
|
Розничная цена на рынке за 1 тонну ($)
|
|
a1
|
Помидоры
|
150÷200
|
310÷320
|
|
a2
|
Огурцы
|
250÷300
|
240÷250
|
|
a3
|
Перец
|
150÷200
|
210÷220
|
|
a4
|
Баклажаны
|
90÷130
|
305÷315
|
|
a5
|
Клубника
|
80÷120
|
748÷908
|
|
a6
|
Бананы
|
46÷50
|
481÷641
|
Как видно из этого перечня, цена на тонну тепличной культуры варьируется в соответствующих пределах. Для каждой i-й культуры она может, скажем, принимать 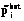 - низкое,
- низкое, 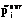 - среднее и
- среднее и 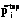 - высокое значения. Изменения в уровне цен в ту или иную сторону делают производителя богаче или беднее.
- высокое значения. Изменения в уровне цен в ту или иную сторону делают производителя богаче или беднее.
Чтобы построить вербальную модель, разобьем объемы прибыли от реализации парниковых культур по уровням: 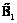 – низкий,
– низкий,  – ниже среднего,
– ниже среднего, 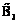 – средний,
– средний,  – выше среднего и
– выше среднего и  – высокий. Тогда, опираясь на данные об урожайности и розничных ценах на тепличные культуры (табл. 1), упорядочим возможные минимальные и максимальные прибыли в $ США в расчете на соответствующие посевные парниковые площади (табл. 2).
– высокий. Тогда, опираясь на данные об урожайности и розничных ценах на тепличные культуры (табл. 1), упорядочим возможные минимальные и максимальные прибыли в $ США в расчете на соответствующие посевные парниковые площади (табл. 2).
Таблица 2
Минимальные и максимальные прибыли от реализации тепличных культур ($)
|
Культура
|
10 га
(низкая прибыль)
|
20 га
(ниже среднего)
|
…
|
50 га (высокая прибыль)
|
|
Min
|
Max
|
Min
|
Max
|
Min
|
Max
|
|
Помидоры
|
465000
|
640000
|
930000
|
1280000
|
2325000
|
3200000
|
|
Огурцы
|
600000
|
750000
|
1200000
|
1500000
|
3000000
|
3750000
|
|
Перец
|
315000
|
440000
|
630000
|
880000
|
1575000
|
2200000
|
|
Баклажаны
|
274500
|
409500
|
549000
|
819000
|
1372500
|
2047500
|
|
Клубника
|
598400
|
1089600
|
1196800
|
2179200
|
2992000
|
5448000
|
|
Бананы
|
221260
|
320500
|
442520
|
641000
|
1106300
|
1602500
|
|
Итого:
|
221260
|
1089600
|
442520
|
2179200
|
1106300
|
5448000
|
В таблице 2 видим, что, если, например, на 10 га выращивать только бананы, то при пессимистическом прогнозе, когда урожайность будет 46 т с одного га, а цена минимальная ($481,00), прибыль составит $221,260.00. Аналогично максимальная прибыль составит $1,089,600.00, если на 10 га выращивать только клубнику при оптимистическом прогнозе на ее урожайность и розничные цены (соответственно 120 т и $908,00).
Для построения функциональной зависимости между эндогенной категорией «полезность» от распределительных наборов, принимающей значения 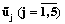 (низкий, ниже среднего, средний, выше среднего и высокий) и экзогенными величинами «цена на тепличные культуры» и «прибыль» в программной оболочке MATLAB/Fuzzy Logic Toolbox было использовано достаточное количество непротиворечивых импликативных правил, где фаззификация входных нечетких терм-множеств проведена на основе гауссовской функции принадлежности, а дефаззификация нечетких выводов (нечетких уровней полезности) – на основе центроидного метода. В частности, при варьируемых ценах на парниковые культуры определены дефаззифицированные уровни (значения) полезности от представленных в таблице 3 распределительных наборов. В данном случае функция полезности зависит от 7 переменных (уровня прибыли и шести цен на культуры), поэтому принимаемые ею значения будут разбросаны в положительном квадранте семимерного гиперпространства. Приведенные в таблице данные (прибыль, варьируемая в интервале [$221260; $5448000], и розничные цены из таблицы 1) масштабированы на отрезке [0, 1].
(низкий, ниже среднего, средний, выше среднего и высокий) и экзогенными величинами «цена на тепличные культуры» и «прибыль» в программной оболочке MATLAB/Fuzzy Logic Toolbox было использовано достаточное количество непротиворечивых импликативных правил, где фаззификация входных нечетких терм-множеств проведена на основе гауссовской функции принадлежности, а дефаззификация нечетких выводов (нечетких уровней полезности) – на основе центроидного метода. В частности, при варьируемых ценах на парниковые культуры определены дефаззифицированные уровни (значения) полезности от представленных в таблице 3 распределительных наборов. В данном случае функция полезности зависит от 7 переменных (уровня прибыли и шести цен на культуры), поэтому принимаемые ею значения будут разбросаны в положительном квадранте семимерного гиперпространства. Приведенные в таблице данные (прибыль, варьируемая в интервале [$221260; $5448000], и розничные цены из таблицы 1) масштабированы на отрезке [0, 1].
Таблица 3
Полезность от потребления произвольных наборов парниковых культур
|
№
п/п
|
Прибыль ($) и ее эквивалент
|
Распределительные наборы и соответствующие данному раскладу эквиваленты розничных цен в масштабе единичного отрезка
|
Полезность
U (у.е.)
|
|
x1/P1
|
x2/P2
|
x3/P3
|
x4/P4
|
x5/P5
|
x6/P6
|
|
1
|
238590
|
80
|
120
|
65
|
140
|
90
|
110
|
|
| |
0.00332
|
0.2
|
0.3
|
0.4
|
0.6
|
0.38750
|
0.06875
|
0.671
|
|
2
|
312320
|
110
|
90
|
95
|
120
|
160
|
140
|
|
| |
0.01742
|
0.2
|
0.3
|
0.4
|
0.6
|
0.38750
|
0.06875
|
0.671
|
|
3
|
323935
|
110
|
90
|
95
|
120
|
160
|
140
|
|
| |
0.01964
|
0.8
|
0.5
|
0.5
|
0.9
|
0.6375
|
0.24375
|
0.405
|
|
4
|
399200
|
150
|
190
|
110
|
170
|
150
|
180
|
|
| |
0.03404
|
0.7
|
0.7
|
0.6
|
0.3
|
0.95
|
0.24375
|
0.323
|
|
5
|
496690
|
180
|
210
|
180
|
160
|
210
|
210
|
|
| |
0.05270
|
0.9
|
0.3
|
0.3
|
0.5
|
0.63750
|
0.61875
|
0.456
|
|
…
|
|
22
|
3914560
|
1350
|
1380
|
1450
|
1450
|
1550
|
1560
|
|
| |
0.70662
|
0.3
|
0.7
|
0.8
|
0.5
|
0.98125
|
0.93125
|
0.39
|
|
23
|
4223270
|
1450
|
1480
|
1550
|
1550
|
1650
|
1760
|
|
| |
0.76568
|
0.2
|
0.9
|
0.9
|
0.9
|
0.95
|
0.86875
|
0.352
|
|
24
|
4667440
|
1550
|
1680
|
1750
|
1750
|
1850
|
1960
|
|
| |
0.85066
|
0.7
|
0.3
|
0.8
|
0.6
|
0.8875
|
0.80625
|
0.343
|
|
25
|
5282480
|
1850
|
1780
|
1750
|
1850
|
2150
|
2260
|
|
| |
0.96833
|
0.2
|
0.6
|
0.7
|
0.5
|
0.91875
|
0.8375
|
0.386
|
|
26
|
5445700
|
1860
|
1790
|
1550
|
2050
|
2160
|
2360
|
|
| |
0.99956
|
0.7
|
0.7
|
0.6
|
0.6
|
0.98125
|
0.93125
|
0.326
|
Полученная на основе реализованных нечетких импликативных правил следующая выборка «набор – полезность»
 (7)
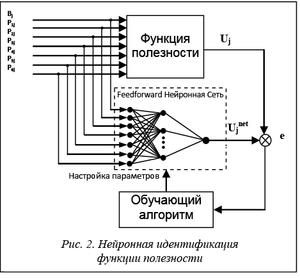
(7)
использована для нейронной идентификации функции полезности для каждого уровня прибыли в отдельности. Для этого применена feedforward нейронная сеть с одним нелинейным скрытым слоем (рис. 2).
На своем выходе нейронная сеть для каждого j-го набора индицирует сигнал
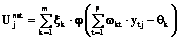 (
(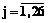 ), (8)
), (8)
где 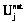 – полезность от j-го набора; p – число нелинейных нейронов в скрытом слое; xk – вес k-й выходной синоптической связи; j(×) – нелинейная функция активации нейронов из скрытого слоя, например, сигмоидного типа:
– полезность от j-го набора; p – число нелинейных нейронов в скрытом слое; xk – вес k-й выходной синоптической связи; j(×) – нелинейная функция активации нейронов из скрытого слоя, например, сигмоидного типа: 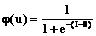 ; wkt – вес связи между k-м нейроном из скрытого слоя и t-м входным нейроном; qk – порог k-го нелинейного нейрона из скрытого слоя; ytj – t-я по счету характеристика j-го набора. После обучения на основе, например, алгоритма error backpropagation нейронную сеть (8) с оптимальными параметрами
; wkt – вес связи между k-м нейроном из скрытого слоя и t-м входным нейроном; qk – порог k-го нелинейного нейрона из скрытого слоя; ytj – t-я по счету характеристика j-го набора. После обучения на основе, например, алгоритма error backpropagation нейронную сеть (8) с оптимальными параметрами 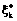 ,
, 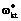 и
и  можно использовать как нелинейную целевую функцию в задаче математического программирования для нахождения оптимального распределения посевных площадей парниковых культур: (s1, s2, …, s6). Зная урожайность каждой из культур (табл. 1), для каждого уровня прибыли последнее можно легко вычислить из полученного на основе данного подхода и, например, метода Лагранжа оптимального решения (
можно использовать как нелинейную целевую функцию в задаче математического программирования для нахождения оптимального распределения посевных площадей парниковых культур: (s1, s2, …, s6). Зная урожайность каждой из культур (табл. 1), для каждого уровня прибыли последнее можно легко вычислить из полученного на основе данного подхода и, например, метода Лагранжа оптимального решения (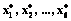 ).
).
На основе нейронечеткого подхода для конкретного желаемого уровня прибыли авторами предложена методика формализации целевой функции полезности для оптимального распределения посевных площадей под сельскохозяйственные культуры. Предлагаемый подход позволяет фермеру заранее определить уровень своей кредитоспособности в рамках сельскохозяйственной деятельности.
Литература
1. United Nations, Millennium Development Goals, published by UN Information Center in Tehran, Tehran. 2003.
2. Mohammad Saeid Nouri Naini, the World's Strategy for Food Security, Quarterly of Social Security, No. 2, pp. 317–342.
3. Интрилигатор М. Математические методы оптимизации и экономическая теория; [пер. с англ.]; под ред. А.А. Конюса. М.: Прогресс, 1975. 606 с.
4. Иманов К.Д., Рзаев Р.Р., Маммадов К.М. Нечеткий подход к моделированию потребительского спроса // Проблемы кибернетики и информатики (PCI–2006): матер. Междунар. конф. (24–26 октября 2006 г., Баку). Баку: Изд-во «Елм», 2006. Т. III. С. 101–104.



 , (4)
, (4)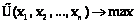 , (5)
, (5) – нечеткая рыночная цена i-й тепличной культуры;
– нечеткая рыночная цена i-й тепличной культуры; 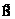 – нечеткая прибыль производителя. Функциональную зависимость в модели (4)–(5), заданную в неявном виде, определим путем построения нечетких правил, где лингвистическую переменную «полезность» будем считать эндогенной величиной, а «прибыль производителя» и «рыночные цены» на тепличные культуры рассматривать как экзогенные лингвистические переменные. В конечном итоге задачей является построение семейства нечетких уровней полезности от реализуемых распределительных наборов парниковых культур, дефаззифицированные значения которых и будут значениями искомой функции полезности.
– нечеткая прибыль производителя. Функциональную зависимость в модели (4)–(5), заданную в неявном виде, определим путем построения нечетких правил, где лингвистическую переменную «полезность» будем считать эндогенной величиной, а «прибыль производителя» и «рыночные цены» на тепличные культуры рассматривать как экзогенные лингвистические переменные. В конечном итоге задачей является построение семейства нечетких уровней полезности от реализуемых распределительных наборов парниковых культур, дефаззифицированные значения которых и будут значениями искомой функции полезности.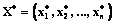 . Тогда функциональную зависимость в модели (4)–(5) представим в виде достаточного набора нечетких правил вида
. Тогда функциональную зависимость в модели (4)–(5) представим в виде достаточного набора нечетких правил вида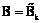 и
и 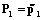 и
и 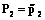
 , то
, то 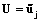 , (6)
, (6) (k=1÷q) – нечеткий k-й уровень прибыли производителя;
(k=1÷q) – нечеткий k-й уровень прибыли производителя; 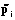 (i=1÷n) – нечеткий уровень цены на i-ю культуру;
(i=1÷n) – нечеткий уровень цены на i-ю культуру; 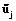 – j-е нечеткое значение критерия полезности U.
– j-е нечеткое значение критерия полезности U.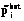 - низкое,
- низкое, 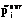 - среднее и
- среднее и 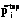 - высокое значения. Изменения в уровне цен в ту или иную сторону делают производителя богаче или беднее.
- высокое значения. Изменения в уровне цен в ту или иную сторону делают производителя богаче или беднее.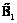 – низкий,
– низкий,  – ниже среднего,
– ниже среднего, 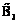 – средний,
– средний,  – выше среднего и
– выше среднего и  – высокий. Тогда, опираясь на данные об урожайности и розничных ценах на тепличные культуры (табл. 1), упорядочим возможные минимальные и максимальные прибыли в $ США в расчете на соответствующие посевные парниковые площади (табл. 2).
– высокий. Тогда, опираясь на данные об урожайности и розничных ценах на тепличные культуры (табл. 1), упорядочим возможные минимальные и максимальные прибыли в $ США в расчете на соответствующие посевные парниковые площади (табл. 2).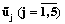 (низкий, ниже среднего, средний, выше среднего и высокий) и экзогенными величинами «цена на тепличные культуры» и «прибыль» в программной оболочке MATLAB/Fuzzy Logic Toolbox было использовано достаточное количество непротиворечивых импликативных правил, где фаззификация входных нечетких терм-множеств проведена на основе гауссовской функции принадлежности, а дефаззификация нечетких выводов (нечетких уровней полезности) – на основе центроидного метода. В частности, при варьируемых ценах на парниковые культуры определены дефаззифицированные уровни (значения) полезности от представленных в таблице 3 распределительных наборов. В данном случае функция полезности зависит от 7 переменных (уровня прибыли и шести цен на культуры), поэтому принимаемые ею значения будут разбросаны в положительном квадранте семимерного гиперпространства. Приведенные в таблице данные (прибыль, варьируемая в интервале [$221260; $5448000], и розничные цены из таблицы 1) масштабированы на отрезке [0, 1].
(низкий, ниже среднего, средний, выше среднего и высокий) и экзогенными величинами «цена на тепличные культуры» и «прибыль» в программной оболочке MATLAB/Fuzzy Logic Toolbox было использовано достаточное количество непротиворечивых импликативных правил, где фаззификация входных нечетких терм-множеств проведена на основе гауссовской функции принадлежности, а дефаззификация нечетких выводов (нечетких уровней полезности) – на основе центроидного метода. В частности, при варьируемых ценах на парниковые культуры определены дефаззифицированные уровни (значения) полезности от представленных в таблице 3 распределительных наборов. В данном случае функция полезности зависит от 7 переменных (уровня прибыли и шести цен на культуры), поэтому принимаемые ею значения будут разбросаны в положительном квадранте семимерного гиперпространства. Приведенные в таблице данные (прибыль, варьируемая в интервале [$221260; $5448000], и розничные цены из таблицы 1) масштабированы на отрезке [0, 1]. (7)
(7)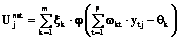 (
(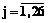 ), (8)
), (8)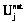 – полезность от j-го набора; p – число нелинейных нейронов в скрытом слое; xk – вес k-й выходной синоптической связи; j(×) – нелинейная функция активации нейронов из скрытого слоя, например, сигмоидного типа:
– полезность от j-го набора; p – число нелинейных нейронов в скрытом слое; xk – вес k-й выходной синоптической связи; j(×) – нелинейная функция активации нейронов из скрытого слоя, например, сигмоидного типа: 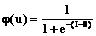 ; wkt – вес связи между k-м нейроном из скрытого слоя и t-м входным нейроном; qk – порог k-го нелинейного нейрона из скрытого слоя; ytj – t-я по счету характеристика j-го набора. После обучения на основе, например, алгоритма error backpropagation нейронную сеть (8) с оптимальными параметрами
; wkt – вес связи между k-м нейроном из скрытого слоя и t-м входным нейроном; qk – порог k-го нелинейного нейрона из скрытого слоя; ytj – t-я по счету характеристика j-го набора. После обучения на основе, например, алгоритма error backpropagation нейронную сеть (8) с оптимальными параметрами 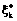 ,
, 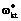 и
и  можно использовать как нелинейную целевую функцию в задаче математического программирования для нахождения оптимального распределения посевных площадей парниковых культур: (s1, s2, …, s6). Зная урожайность каждой из культур (табл. 1), для каждого уровня прибыли последнее можно легко вычислить из полученного на основе данного подхода и, например, метода Лагранжа оптимального решения (
можно использовать как нелинейную целевую функцию в задаче математического программирования для нахождения оптимального распределения посевных площадей парниковых культур: (s1, s2, …, s6). Зная урожайность каждой из культур (табл. 1), для каждого уровня прибыли последнее можно легко вычислить из полученного на основе данного подхода и, например, метода Лагранжа оптимального решения (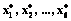 ).
).