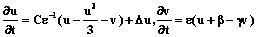Для описания автоволновых процессов в нелинейных динамических системах в настоящее время принято использовать системы нелинейных дифференциальных уравнений в частных производных параболического типа [1]:
 , (1)
, (1)
где Ei – переменная; Fi – нелинейная функция; Di – коэффициент диффузии.
В двухмерном случае система уравнений имеет вид  ,
,
 . (2)
. (2)
Уравнение (1) является более общим, чем (2). В данной работе реализован программный комплекс для расчета режимов нелинейных динамических систем с помощью множества глобально связанных осцилляторов, поскольку он позволяет учесть не только диффузионные связи, но и связи более общего характера.
Точечной системой для (1) является система обыкновенных дифференциальных уравнений
 . (3)
. (3)
Для автоволновых процессов такие системы дифференциальных уравнений жесткие, их исследование требует применения специальных методов.
Гетерогенность и сложная структура областей моделирования значительно усложняют программу и увеличивают время счета. Для повышения эффективности решения с учетом особенностей вычислительной среды MATLAB разработан алгоритм сканирования, основанный на сканировании области.
Сформулируем алгоритм сканирования применительно к нахождению приближенных решений уравнения с использованием сеточного метода прямых, что приведет к системе обыкновенных дифференциальных уравнений. Образование траекторий сканирования рассмотрим для случая прямоугольной области D с узлами на пересечении линий прямоугольной сетки Aij(iDx, jDy), i=1, …, N1, j=1, …, N2 (общее число точек равно N=N1N2). Считаем Dx=Dy=1.
1. 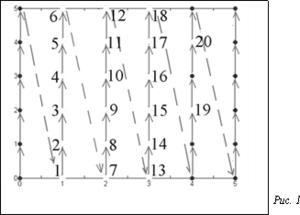 Все элементы AijÎD, i=1, …, N1, j=1, …, N2, последовательно располагаются на ведущей траектории S, получаемой сканированием области D (подобно телевизионной развертке или любой другой), и последовательно нумеруются числами натурального ряда. Предполагается, что SÌD является компактным множеством в D. При сканировании каждой точке AijÎD, i=1, …, N1, j=1, …, N2, ставится в однозначное соответствие натуральный номер k=1, …, N на траектории сканирования. Пример траектории сканирования для двухмерной области представлен на рисунке 1. Таким образом, между точками Aij и точками с номером k на траектории сканирования задается однозначное преобразование L: L(Aij)=k.
Все элементы AijÎD, i=1, …, N1, j=1, …, N2, последовательно располагаются на ведущей траектории S, получаемой сканированием области D (подобно телевизионной развертке или любой другой), и последовательно нумеруются числами натурального ряда. Предполагается, что SÌD является компактным множеством в D. При сканировании каждой точке AijÎD, i=1, …, N1, j=1, …, N2, ставится в однозначное соответствие натуральный номер k=1, …, N на траектории сканирования. Пример траектории сканирования для двухмерной области представлен на рисунке 1. Таким образом, между точками Aij и точками с номером k на траектории сканирования задается однозначное преобразование L: L(Aij)=k.
2. Создается еще l траекторий сканирования Si, i=1, …, l, назовем их вспомогательными (для прямоугольной сетки l=4), которые предназначены для учета связи элемента AijÎD, i=1, …, N1, j=1, …, N2, с соседними. На вспомогательных траекториях Si, i=1, …, l, указываются номера соседних элементов, с которыми связан элемент An, nÎN, на ведущей траектории S в предположении, что соответствующий соседний элемент вспомогательной траектории является элементом ведущей траектории.
3. Метод интегрируется с программной средой MATLAB, граница Г области D определяется средствами MATLAB путем предварительной маркировки области D.
4. Для учета граничных условий создается еще одна траектория сканирования, аналогичная ведущей, назовем ее граничной, и содержащая N элементов. Если точка лежит на границе  , ей присваивается соответствующий номер
, ей присваивается соответствующий номер  ведущей траектории, а всем другим точкам – номер k=0.
ведущей траектории, а всем другим точкам – номер k=0.
5. Для учета гетерогенности области D на ведущей и вспомогательных траекториях наносятся номера точек соответствующей области. Учет наличия границ между областями производится с помощью граничной траектории, как в п. 4.
6. С помощью вспомогательной предпрограммы, работающей до основной программы, создаются ведущая траектория, вспомогательные траектории сканирования, учитываются граничные условия, определяется граница Г области D.
7. Выполняется расчет членов, обусловленных диффузионными связями, а также переменных, продиктованных граничными условиями и гетерогенностью области D. Эти расчеты производятся в основной программе с помощью ведущей, вспомогательных и граничной траекторий сканирования. Практически в выбранной системе программирования MATLAB составляется одномерный вектор правых частей системы нелинейных дифференциальных уравнений (1). Полученный одномерный вектор используется в качестве входных данных для решения жестких систем дифференциальных уравнений (1) средствами MATLAB, с которыми интегрируется метод сканирования.
8. Обратным преобразованием, имеющим вид L–1: L–1(k)=Aij, по известной ведущей траектории и расположению ее элементов в области D полученные с помощью MATLAB решения системы (1) для элементов ведущей траектории отображаются на исходную область D.
 С учетом особенностей точечной системы (3) использовался сеточный метод прямых в сочетании с программной средой MATLAB, позволяющей эффективно решать жесткие системы нелинейных дифференциальных уравнений вида (3). Исследовать автоволновые процессы в активных средах можно, используя граничные условия Дирихле, Неймана, смешанные граничные условия. Для этого реализован вычислительный алгоритм со связью с ближайшими соседями. Введем обозначение для суммарной связи в виде Si. В двухмерном случае использовался алгоритм
С учетом особенностей точечной системы (3) использовался сеточный метод прямых в сочетании с программной средой MATLAB, позволяющей эффективно решать жесткие системы нелинейных дифференциальных уравнений вида (3). Исследовать автоволновые процессы в активных средах можно, используя граничные условия Дирихле, Неймана, смешанные граничные условия. Для этого реализован вычислительный алгоритм со связью с ближайшими соседями. Введем обозначение для суммарной связи в виде Si. В двухмерном случае использовался алгоритм
 , (4)
, (4)
где R – оператор Рунге–Кутта четвертого порядка; n, m – число элементов по горизонтали и вертикали; U=(U11, …, Uij, …, Unm) – вектор начальных условий [2–4]. В формуле (4) Fij – блоки правых частей дифференциальных уравнений точечных элементов возбудимой ткани. При этом
 .
.
Значение Sij можно вычислить в виде
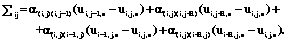
С помощью функций Fij, i=1, …, n, j=1, …, m, формируется вектор, используемый в вычислительной среде MATLAB для численного решения систем дифференциальных уравнений. Частью этого вектора является набор начальных условий. Использование программных средств MATLAB позволяет решать большие системы жестких нелинейных дифференциальных уравнений (порядка 100 000). Была разработана вычислительная система, блок-схема которой показана на рисун- ке 2.
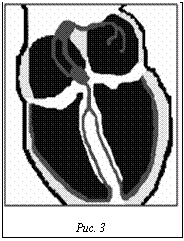 При работе созданной вычислительной системы область моделирования представляется в ви- де цветного файла-картинки с расширением .gif (рис. 3, моделируемая область – проводящая система сердца).
При работе созданной вычислительной системы область моделирования представляется в ви- де цветного файла-картинки с расширением .gif (рис. 3, моделируемая область – проводящая система сердца).
Каждая точка картинки на рисунке 3 соответствует точке моделируемой области. Устанавливая цвет для точек картинки, задается набор параметров, которым должна обладать соответствующая точка моделируемой области. К примеру, в простейшем случае можно красным цветом выделить точки, принадлежащие области, и любым другим – не принадлежащие ей. В процессе предподготовки с помощью специального преобразования по файлу-картинке формируются ведущая и вспомогательные траектории сканирования. На их основании по описанному выше алгоритму формируются и решаются системы обыкновенных дифференциальных уравнений. Результат выводится в виде последовательно сменяющихся кадров, отображающих решение системы с заданным дискретным шагом. Можно сохранить решение как видеоролик.
Использование описанного метода сканирования в вычислительной системе для моделирования автоволновых процессов позволяет:
1) эффективно учитывать любые граничные условия (Неймана, Дирихле, смешанные), а также гетерогенность области, в которой производится исследование;
2) исследовать системы с жесткими переменными по времени и пространственным координатам;
3) учитывать любые глобальные связи в задачах исследования многих глобально связанных осцилляторов (диффузионные связи с ближайшими соседями – частный случай глобальных связей);
4) значительно упрощать базовую программу вычислений за счет удаления большого количества условных операторов, учитывающих граничные условия и гетерогенность области;
5) значительно сокращать время вычислений в случаях сложных границ области;
6) применять свободные граничные условия;
7) быстро модифицировать программы при идентификации математической модели динамической системы.
С помощью вычислительного комплекса исследовалось взаимодействие волн различного типа в активных средах. В качестве математических моделей точечных элементов выбраны нелинейные дифференциальные уравнения Ван дер Поля–Фитцхъюга
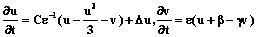
с параметрами e=0,03, b=0,7, g=0,8.
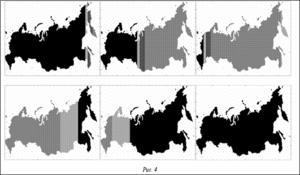
Для примера моделирования сложной формы взят расчет распространения автоволн в области, близкой по контуру к карте Российской Федерации (рис. 4). Как видно из рисунка, используемый алгоритм позволяет моделировать область с границами любой сложности.
Описанная вычислительная система допускает модификацию на основе метода сканирования для приближенного решения нелинейных дифференциальных уравнений в частных производных параболического типа в гетерогенных областях со сложной границей [5].
В статье рассмотрен вычислительный комплекс для моделирования автоволновых процессов, описываемых дифференциальными уравнениями в частных производных параболического типа, в гетерогенных областях со сложной границей. Для подобного решения используется метод сканирования. Вычислительные эксперименты показали эффективность применения данного метода в вычислительном комплексе для моделирования автоволновых процессов.
Литература
1. Мазуров М.Е. Нелинейная синхронизация и ритмогенез в электровозбудимых системах сердца: дисс. докт. физ.-мат. наук. Пущино, 2007.
2. Математические вопросы численного решения гиперболических уравнений. М.: Физматгиз, 2001. 608 с.
3. Березин И.С., Жидков Н.П. Методы вычислений. Т. 2. М.: Изд-во Физматлит, 1962.
4. Erwin Stein, Ren De Borst, Thomas J.R. Hughes. Encyclopedia of Computational Mechanics. URL: http://www.dealtime.com/Encyclopedia_Of_Computational_Mechanics_by_Erwin_Stein/info (дата обращения 20.01.2011).
5. Мазуров М.Е., Калюжный И.М. О методе сканирования при решении граничных задач для нелинейных уравнений параболического типа в гетерогенных областях сложной геометрии. М.: ООО САИТ, 2009.
 , (1)
, (1) ,
, . (2)
. (2) . (3)
. (3)
 , ей присваивается соответствующий номер
, ей присваивается соответствующий номер  ведущей траектории, а всем другим точкам – номер k=0.
ведущей траектории, а всем другим точкам – номер k=0. С учетом особенностей точечной системы (3) использовался сеточный метод прямых в сочетании с программной средой MATLAB, позволяющей эффективно решать жесткие системы нелинейных дифференциальных уравнений вида (3). Исследовать автоволновые процессы в активных средах можно, используя граничные условия Дирихле, Неймана, смешанные граничные условия. Для этого реализован вычислительный алгоритм со связью с ближайшими соседями. Введем обозначение для суммарной связи в виде Si. В двухмерном случае использовался алгоритм
С учетом особенностей точечной системы (3) использовался сеточный метод прямых в сочетании с программной средой MATLAB, позволяющей эффективно решать жесткие системы нелинейных дифференциальных уравнений вида (3). Исследовать автоволновые процессы в активных средах можно, используя граничные условия Дирихле, Неймана, смешанные граничные условия. Для этого реализован вычислительный алгоритм со связью с ближайшими соседями. Введем обозначение для суммарной связи в виде Si. В двухмерном случае использовался алгоритм , (4)
, (4) .
.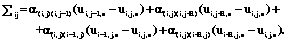
 При работе созданной вычислительной системы область моделирования представляется в ви- де цветного файла-картинки с расширением .gif (рис. 3, моделируемая область – проводящая система сердца).
При работе созданной вычислительной системы область моделирования представляется в ви- де цветного файла-картинки с расширением .gif (рис. 3, моделируемая область – проводящая система сердца).