Моделирование процесса первичного выхода заряда (относительной концентрации дырок, избежавших начальной рекомбинации) в окисле под действием ионизирующего излучения (ИИ) необходимо для оценки сдвига порогового напряжения в полупроводниковых элементах на основе структур металл–диэлектрик–полупроводник (МДП), приводящего к функционально-параметрическим отказам изделий. В настоящей работе рассматривается ПО на основе приложения MathCAD, позволяющее оперативно в интерактивном режиме изменять входные и выходные параметры в графическом и аналитическом виде, условия моделирования и математические модели для выхода заряда и дрейфового ионизационного тока в SiO2.
Используемая для выхода заряда (f) модель учитывает влияние напряженности электрического поля, температуры, мощности поглощенной дозы и энергии ИИ [1]. Она основана на MSR-модели (multiple shape recombination) электронно-дырочной рекомбинации в окисле [2]. В зависимости от энергии фотонов MSR-модель предполагает образование в окисле нескольких видов активированных областей.
1. Spur (шпора). Характерна для SiO2 при облучении фотонами с энергией в диапазоне 10÷70 эВ. Дефект возникает при дистанционном взаимодействии вторичных электронов с молекулами окисла. Такое низкоэнергетическое взаимодействие приводит к образованию активированной области практически сферической формы, радиус которой (0,6÷0,8)∙10-8 м при средней энергии вторичных электронов 40 эВ.
2. Blob (капля). Дефекты, которые образуются под действием вторичных электронов с энергией 80÷150 эВ в виде экситонных пар, как и в случае предыдущего вида дефектов spur. При таком низкоэнергетическом воздействии электрон удерживается около дырки, в паре с которой был образован, силой кулоновского притяжения. Облачко электронов в области дефектообразования, теряя со временем энергию, образует практически сферические области перекрывающихся дефектов. Радиусы сферических областей определяются расстоянием, на котором потенциальная энергия электростатического кулоновского взаимодействия электрона с дыркой равна энергии теплового движения электрона. Этот радиус равен радиусу Онзагера и для SiO2 при комнатной температуре составляет около 10-8 м.
3. Short track (короткий след). Создается вторичными электронами с энергией в диапазоне от 150 эВ до 5 кэВ. Траектория этих электронов относительно прямолинейна, поскольку сила кулоновского взаимодействия электрона с дыркой, в паре с которой он был образован, пренебрежимо мала. Полное преобразование энергии вторичных электронов в этом виде радиационных дефектов можно разделить на три этапа. Половина энергии электрона теряется в процессе низкоэнергетического взаимодействия с молекулой SiO2, в результате образуется активированная область цилиндрической формы из перекрывающихся дефектов. Радиус цилиндрической области равен радиусу дефектов типа spur. Доля энергии вторичных электронов, расходуемая на высокоэнергетическое взаимодействие, приводит к образованию перекрывающихся коротких треков. В конце короткого трека, когда энергия электрона становится меньше 150 эВ, происходит дефектообразование типа blob. Этот вид радиационных дефектов получил также название column.
4. Branch track (разветвленный след). Дефекты такого рода подобны дефектам short track. Существенное отличие в том, что в дефектах branch track активированные области не перекрывают друг друга. В конце branch track, когда энергия вторичного электрона становится меньше 5 кэВ, его энергия преобразуется во внутреннюю энергию в процессе образования дефектов типа short track. Этот вид радиационных дефектов получил также название isolated spur.
Для определения f в программе используется модель
 , (1)
, (1)
где n0i – концентрация активированных электронов (или дырок) в области i-го вида радиационного дефекта (blob, column или isolated spur); m=3 – количество типов радиационных дефектов; αi – коэффициент, определяющий долю начальной энергии вторичных электронов, теряемую на образование i-го вида радиационного дефекта; di – диаметр i-го вида радиационных дефектов (наименьшее расстояние, которое должен преодолеть электрон, чтобы покинуть активированную область); То, Т – соответственно комнатная и текущая температура (То=300 К); ξ – коэффициент, определяемый для каждого вида радиационного дефекта, ξ= –1 для i=1 и ξ=3 для i=2, 3; l0i, li – характеристическая длина электронов при комнатной и текущей температуре соответственно. Величины δ и λ определяются выражениями  ;
;  , где μ0 – подвижность электронов в окисле при комнатной температуре (см2 В-1 с-1) и E=0; с – коэффициент; Eg – ширина запрещенной зоны для прямых переходов; Е – напряженность электрического поля в окисле; g – эффективность ионизации; Pγ – мощность дозы ИИ [1].
, где μ0 – подвижность электронов в окисле при комнатной температуре (см2 В-1 с-1) и E=0; с – коэффициент; Eg – ширина запрещенной зоны для прямых переходов; Е – напряженность электрического поля в окисле; g – эффективность ионизации; Pγ – мощность дозы ИИ [1].
Концентрация неравновесных носителей заряда (НЗ), образующихся в каждой из активированных областей, определяется на основе диффузионно-дрейфового приближения:
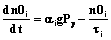 , (2)
, (2)
где n0i – концентрация активированных электронов (или дырок) в области i-го вида радиационного дефекта (blob, column или isolated spur); τi – время жизни электронов для i-го вида радиационного эффекта.
Начальное условие: t=0, n0i=0. Уравнение (2) является нелинейным, так как время жизни зависит от концентрации электронов, поэтому для его решения необходимо использовать численные методы. В предлагаемой программе используется явный метод Эйлера.
Для импульсного ИИ мощность дозы определяется выражением
 (3)
(3)
где PγMAX – пиковое значение мощности дозы; τИ – длительность импульса ИИ.
Для диаметров радиационных дефектов в [2] приняты выражения
 (4)
(4)
Величина rblob определяется как радиус Онзагера из условия равенства тепловой и потенциальной энергии электрона в электростатическом поле дырки. Для произвольной температуры Т используется выражение  [1].
[1].
Значения rblob0, rcolumn и rspur определены на основе экспериментальных данных, их значения равны 10-8 м [2].
Для подвижности электронов в SiO2 используется выражение
 , (5)
, (5)
где Vα – дрейфовая скорость движения электронов в окисле (см∙с-1); χ – коэффициент; k=1,38∙10-23 Дж∙К-1 – постоянная Больцмана; qe=1,6∙10-19 Кл – элементарный заряд [1].
Выражение для μ получено из предположения о том, что подвижность электронов в основном ограничена рассеянием на фононах.
Время жизни электронов определяется межзонной излучательной рекомбинацией, при этом для исследуемых энергий фотонов наиболее вероятны прямые переходы
 . (6)
. (6)
 Величина Eg определяется с учетом температуры окисла и эффекта термоэлектрической ионизации (эффект Френкеля):
Величина Eg определяется с учетом температуры окисла и эффекта термоэлектрической ионизации (эффект Френкеля):
 , (7)
, (7)
где Eg0 – ширина запрещенной зоны при комнатной температуре, для SiO2 Eg0=8 эВ; ∆Т=Т-То.
Эффективность ионизации зависит от температуры окисла и напряженности внешнего электрического поля:
 , (8)
, (8)
где g0=5,9∙1012 см-3 рад-1; с – эффективность ионизации при комнатной температуре и отсутствии внешнего электрического поля.
Характеристическая длина электронов для i-го вида радиационного дефекта определяется по формуле  .
.
Величины μ0 и с вычисляются на основе экспериментальных данных, полученных для воздействия стационарного ИИ:
 . (9)
. (9)
Решая (9), находим δ для известного экспериментального значения f0. Для наилучшего совпадения расчетных и экспериментальных данных величина δ определяется для каждой энергии излучения отдельно.
На основе рассчитанного значения f вычисляется дрейфовая составляющая плотности ионизационного тока окисла: j=qemfnE.
 Зависимость f от мощности экспозиционной дозы, энергии квантов ИИ и температуры окисла делает необходимым определение эквивалентных по ионизационной реакции МДП-приборов экспозиционных доз для двух ИИ с различными характеристиками. Такая проблема может возникнуть при проведении аттестационных или определительных испытаний на моделирующих установках, параметры которых по различным причинам не могут соответствовать параметрам реальных источников ИИ (например, по причине ограничения времени). Эта задача наиболее актуальна при исследованиях на воздействие стационарного ИИ. Эквивалентность двух ИИ с различными характеристиками и условиями облучения определяется по модели [1], полученной из условия равенства накапливаемого в окисле заряда:
Зависимость f от мощности экспозиционной дозы, энергии квантов ИИ и температуры окисла делает необходимым определение эквивалентных по ионизационной реакции МДП-приборов экспозиционных доз для двух ИИ с различными характеристиками. Такая проблема может возникнуть при проведении аттестационных или определительных испытаний на моделирующих установках, параметры которых по различным причинам не могут соответствовать параметрам реальных источников ИИ (например, по причине ограничения времени). Эта задача наиболее актуальна при исследованиях на воздействие стационарного ИИ. Эквивалентность двух ИИ с различными характеристиками и условиями облучения определяется по модели [1], полученной из условия равенства накапливаемого в окисле заряда:
 . (10)
. (10)
Фрагмент программы изображен на рисунке 1.
На рисунке 2 представлены экспериментальные данные для комнатной температуры [3], а также показана зависимость относительной концентрации электронов, избежавших рекомбинации, от энергии ИИ и температуры при напряженности электрического поля Е=3∙105 В∙см-1.
 Из рисунка видно, что имеется хорошее совпадение расчетных и экспериментальных данных. При сравнительно высоких энергиях фотонов ИИ повышение температуры приводит к снижению f. Это объясняется увеличением концентрации электронно-дырочных пар из-за увеличения времени жизни и, как следствие, уменьшением характеристической длины электронов. При низкоэнергетическом воздействии температурное влияние на f снижается. Это объясняется тем, что при уменьшении энергии фотонов большая часть поглощенной энергии идет на образование активированных областей типа blobs, для которых характерно уменьшение диаметра с ростом температуры. Этот фактор с ростом температуры способствует увеличению f.
Из рисунка видно, что имеется хорошее совпадение расчетных и экспериментальных данных. При сравнительно высоких энергиях фотонов ИИ повышение температуры приводит к снижению f. Это объясняется увеличением концентрации электронно-дырочных пар из-за увеличения времени жизни и, как следствие, уменьшением характеристической длины электронов. При низкоэнергетическом воздействии температурное влияние на f снижается. Это объясняется тем, что при уменьшении энергии фотонов большая часть поглощенной энергии идет на образование активированных областей типа blobs, для которых характерно уменьшение диаметра с ростом температуры. Этот фактор с ростом температуры способствует увеличению f.
На рисунке 3 показана зависимость доли неравновесных НЗ, избежавших рекомбинации, от напряженности внешнего электрического поля. Из полученных результатов следует, что с увеличением напряженности поля доля электронно-дырочных пар, избежавших рекомбинации, увеличивается. Влияние температуры на зависимость f(E) уменьшается с увеличением напряженности поля. Это объясняется тем, что, во-первых, влияние температуры на f носит разнонаправленный характер, так как с ростом температуры одновременно происходит уменьшение характеристической длины электронов для всех видов активированных областей и уменьшение диаметра для дефектов типа blobs; а, во-вторых, существует более сильная зависимость характеристической длины от напряженности поля (характеристическая длина прямо пропорциональна E и обратно пропорциональна Т3/4).
 На рисунке 4 показана зависимость эквивалентной экспозиционной дозы D2 для γ-квантов с энергией Wγ=1,25 МэВ, мощностью экспозиционной дозы Pγ1=0,07 рад∙с-1 при комнатной температуре и напряженности внешнего электрического поля Е=3∙105 Всм-1 от мощности экспозиционной дозы Pγ2. Из рисунка видно, что при увеличении мощности дозы Pγ2 требуемое эквивалентное значение D2 возрастает нелинейно. При увеличении Pγ2 в 100 раз эквивалентная по величине накопленного заряда экспозиционная доза D2 возрастает на три порядка.
На рисунке 4 показана зависимость эквивалентной экспозиционной дозы D2 для γ-квантов с энергией Wγ=1,25 МэВ, мощностью экспозиционной дозы Pγ1=0,07 рад∙с-1 при комнатной температуре и напряженности внешнего электрического поля Е=3∙105 Всм-1 от мощности экспозиционной дозы Pγ2. Из рисунка видно, что при увеличении мощности дозы Pγ2 требуемое эквивалентное значение D2 возрастает нелинейно. При увеличении Pγ2 в 100 раз эквивалентная по величине накопленного заряда экспозиционная доза D2 возрастает на три порядка.
Таким образом, реализованная в MathCAD программа позволяет проводить исследования величины накапливаемого в окисле заряда и дрейфового ионизационного тока в зависимости от напряженности внешнего электрического поля, температуры, мощности дозы и энергии ИИ, а также определять эквивалентную дозу ИИ в зависимости от условий облучения. Проведенные численные эксперименты показали хорошую согласованность с экспериментальными результатами, полученными для комнатной температуры.
Литература
1. Панюшкин Н.Н., Матвеев Н.Н. Микроуравневая математическая модель для выхода заряда в SiO2 в условиях воздействия ионизирующего излучения // Системы управления и информационные технологии. 2009. № 3 (37). С. 88–92.
2. Dozier C.M. and Brown D.B. Effect of photon energy on response of MOS devices. IEEE Trans. Nucl. Sci. 1981, NS-28, pp. 4137–4142.
3. Dozier C.M. and Brown D.B. Electron-hole recombination in irradiated SiO2 from a microdosimetry viewpoint. IEEE Trans. Nucl. Sci. NS-28, 1981, pp. 4142–4145.
 , (1)
, (1) ;
;  , где μ0 – подвижность электронов в окисле при комнатной температуре (см2 В-1 с-1) и E=0; с – коэффициент; Eg – ширина запрещенной зоны для прямых переходов; Е – напряженность электрического поля в окисле; g – эффективность ионизации; Pγ – мощность дозы ИИ [1].
, где μ0 – подвижность электронов в окисле при комнатной температуре (см2 В-1 с-1) и E=0; с – коэффициент; Eg – ширина запрещенной зоны для прямых переходов; Е – напряженность электрического поля в окисле; g – эффективность ионизации; Pγ – мощность дозы ИИ [1].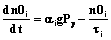 , (2)
, (2) (3)
(3) (4)
(4) [1].
[1]. , (5)
, (5) . (6)
. (6) Величина Eg определяется с учетом температуры окисла и эффекта термоэлектрической ионизации (эффект Френкеля):
Величина Eg определяется с учетом температуры окисла и эффекта термоэлектрической ионизации (эффект Френкеля): , (7)
, (7) , (8)
, (8) .
. . (9)
. (9) Зависимость f от мощности экспозиционной дозы, энергии квантов ИИ и температуры окисла делает необходимым определение эквивалентных по ионизационной реакции МДП-приборов экспозиционных доз для двух ИИ с различными характеристиками. Такая проблема может возникнуть при проведении аттестационных или определительных испытаний на моделирующих установках, параметры которых по различным причинам не могут соответствовать параметрам реальных источников ИИ (например, по причине ограничения времени). Эта задача наиболее актуальна при исследованиях на воздействие стационарного ИИ. Эквивалентность двух ИИ с различными характеристиками и условиями облучения определяется по модели [1], полученной из условия равенства накапливаемого в окисле заряда:
Зависимость f от мощности экспозиционной дозы, энергии квантов ИИ и температуры окисла делает необходимым определение эквивалентных по ионизационной реакции МДП-приборов экспозиционных доз для двух ИИ с различными характеристиками. Такая проблема может возникнуть при проведении аттестационных или определительных испытаний на моделирующих установках, параметры которых по различным причинам не могут соответствовать параметрам реальных источников ИИ (например, по причине ограничения времени). Эта задача наиболее актуальна при исследованиях на воздействие стационарного ИИ. Эквивалентность двух ИИ с различными характеристиками и условиями облучения определяется по модели [1], полученной из условия равенства накапливаемого в окисле заряда: . (10)
. (10)
 На рисунке 4 показана зависимость эквивалентной экспозиционной дозы D2 для γ-квантов с энергией Wγ=1,25 МэВ, мощностью экспозиционной дозы Pγ1=0,07 рад∙с-1 при комнатной температуре и напряженности внешнего электрического поля Е=3∙105 Всм-1 от мощности экспозиционной дозы Pγ2. Из рисунка видно, что при увеличении мощности дозы Pγ2 требуемое эквивалентное значение D2 возрастает нелинейно. При увеличении Pγ2 в 100 раз эквивалентная по величине накопленного заряда экспозиционная доза D2 возрастает на три порядка.
На рисунке 4 показана зависимость эквивалентной экспозиционной дозы D2 для γ-квантов с энергией Wγ=1,25 МэВ, мощностью экспозиционной дозы Pγ1=0,07 рад∙с-1 при комнатной температуре и напряженности внешнего электрического поля Е=3∙105 Всм-1 от мощности экспозиционной дозы Pγ2. Из рисунка видно, что при увеличении мощности дозы Pγ2 требуемое эквивалентное значение D2 возрастает нелинейно. При увеличении Pγ2 в 100 раз эквивалентная по величине накопленного заряда экспозиционная доза D2 возрастает на три порядка.