В настоящее время проводятся широкие исследования в области интеллектуальных мультимодальных интерфейсов [1]. Под модальностью обычно понимается присущая человеку форма воздействия на другого человека или компьютер с помощью речи, жестов, прикосновений, мимики, внешности и т.п. Считается, что человеко-машинный интерфейс является интеллектуальным, даже если в рамках одной формы взаимодействия с компьютером, например, с помощью жестов, могут использоваться различные модальности. При этом возникает задача объединения, или, как часто говорят, агрегирования различных модальностей. Агрегирование может выполняться на двух уровнях – нижнем и верхнем [2]. Будем полагать, что с каждым сигналом Yi[t0, tn]={yi(t0), yi(t1), yi(t2), …, yi(tn)} связана своя модальность (iÎ{1, …, m}, m – число модальностей). Агрегирование, имеющее дело с сигналами, обычно относится к нижнему уровню. Сигналы и соответствующие им модальности на нижнем уровне синхронизированы, взаимосвязь и взаимовлияние сигналов хорошо просматриваются, модальности часто относятся к одной форме воздействия. Агрегирование верхнего уровня обычно осуществляется после работы алгоритмов распознавания нижнего уровня, каждый из которых распознает группы сигналов, относящихся к одной форме воздействия или даже одной модальности. Функции принадлежностей на верхнем уровне могут формироваться с помощью различных моделей. Формы модальностей могут не зависеть от времени.
Например, в алгоритме распознавания динамических жестов с использованием модели, основанной на нечетких конечных автоматах и множествах нечетких эталонных грамматик, для определения сходства (близости) распознаваемого жеста с эталонным используется мера
 , (1)
, (1)
агрегирующая функции принадлежности  языка распознаваемого жеста различным нечетким языкам эталонных жестов как максимум из всех значений этих функций (в данном случае kÎ{1, …, K}, K – число распознаваемых объектов). Обычно подобные агрегирующие функции Ak называют операторами агрегирования. Оператор агрегирования (1) назовем max-оператором. Использование max-оператора для распознавания модальностей обеспечивает высокий уровень надежности, но может быть неэффективным для использования на верхнем уровне.
языка распознаваемого жеста различным нечетким языкам эталонных жестов как максимум из всех значений этих функций (в данном случае kÎ{1, …, K}, K – число распознаваемых объектов). Обычно подобные агрегирующие функции Ak называют операторами агрегирования. Оператор агрегирования (1) назовем max-оператором. Использование max-оператора для распознавания модальностей обеспечивает высокий уровень надежности, но может быть неэффективным для использования на верхнем уровне.
Другим популярным оператором агрегирования, помимо max-оператора, является средневзвешенный арифметический оператор:
 , (2)
, (2)
где wi – весовой коэффициент,  .
.
Агрегирование с помощью средневзвешенного арифметического может приводить к недостаточной надежности (точности) распознавания, понимаемой как процент успешных распознаваний из числа всех попыток. Это может быть следствием эмпиричности выбора весовых коэффициентов wi, а также трудности учета возможной взаимозависимости функций принадлежности.
Тем не менее использование операторов агрегирования зарекомендовало себя как перспективный путь для мультимодального распознавания, которое может преследовать различные цели. Одна из них – управление функционированием виртуальных объектов в интеллектуальном интерфейсе на основе распознанных объектов реального мира. Поэтому основной задачей настоящей статьи является разработка метода нечеткого агрегирования мультимодальной информации, для которого источниками информации являются результаты распознавания объектов алгоритмами нижнего уровня.
Агрегирование модальностей с помощью операторов Сугено и Шоке
Нечеткой мерой называется функция g: 2R®[0, 1], где R – множество каких-либо параметров, характеризующих некоторый объект [3]. Нечеткая мера g(Qi) определяет совокупную значимость параметров, входящих в множество Qi. Нечеткая мера удовлетворяет ряду условий: в частности, g(Æ)=0, g(Y)=1; если Q, PÎY и QÌP, то g(Q)£g(P). Если mi – некоторая функция принадлежности, определяемая на универсуме допустимых отсчетов yiÎYi, i=1, …, m, относящихся к одному промежутку времени, а Y={Y1, …, Ym} – множество модальностей, то нечеткие операторы можно определить следующим образом.
Нечеткий оператор Сугено [4]:
 , (3)
, (3)
где  Qi={Y1, …, Yi}, i=1, …, m.
Qi={Y1, …, Yi}, i=1, …, m.
Нечеткий оператор Шоке [5]:
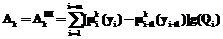 , (4)
, (4)
где 
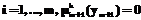 .
.
Наиболее распространены (вследствие простоты) методы вычисления нечеткой меры, основанные на понятии gl-нечеткой меры, введенной Сугено. Нечеткая мера называется gl-нечеткой мерой, если для нее справедливо условие: для всех Q,PÌY, таких, что QÇP=Æ, имеет место g(QÈP)= =g(Q)+g(P)+lg(Q)g(P) для некоторого l>–1.
Рассмотрим процедуру наиболее популярного метода вычисления gl-нечеткой меры [4], обозначая ее по-прежнему просто g.
Шаг 1. Для каждой модальности (сигнала) Yi, i=1, …, m, выбрать значение нечеткой меры g(Yi)Î[0, 1] как степень важности модальности Yi. Значения g(Yi) могут быть установлены экспертом, получены в результате наблюдений или каким-либо другим путем.
Шаг 2. Найти значение l, используя уравнение (5).
 . (5)
. (5)
Шаг 3. Для всех Qi={Y1, …, Yi}, i=1, …, m, вычислить рекурсивно нечеткие меры g(Qi), используя следующие выражения:
g(Q1)=g(Y1),
g(Qi)=g(Yi)+g(Qi–1)+lg(Yi)g(Qi–1), (6)
i=2, …, m.
Метод нечеткого агрегирования мультимодальной информации на основе операторов агрегирования Сугено и Шоке
Рассмотрим сначала процедуру формирования множества Yi и процедуру распознавания отдельным алгоритмом i с помощью функции  .
.
В общем случае исходными для агрегирования являются i алгоритмов, i=1, ..., m, использующих скрытые модальности. В данной работе эти модальности и способы их агрегирования не рассматриваются, используется только результат работы каждого из этих алгоритмов как источник новой отдельной модальности (сигнала) Yi, i=1, ..., m, и функции принадлежности 
 , i=0, ..., m, ji=0, ..., ni. Задачей является агрегирование модальностей Yi, i=0, ..., m. Для того чтобы сформировать множество Yi и функции принадлежности
, i=0, ..., m, ji=0, ..., ni. Задачей является агрегирование модальностей Yi, i=0, ..., m. Для того чтобы сформировать множество Yi и функции принадлежности  i=0, ..., m, ji=0, ..., ni, каждый алгоритм проходит предварительную обработку в соответствии со следующей процедурой 1.
i=0, ..., m, ji=0, ..., ni, каждый алгоритм проходит предварительную обработку в соответствии со следующей процедурой 1.
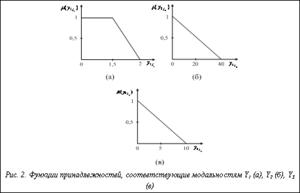
Шаг 1. Задается совокупность пустых множеств  , k=1, …, K.
, k=1, …, K.
Шаг 2. Для каждого эталонного объекта k, k=1, …, K, c использованием скрытых модальностей формируется своя эталонная модель  , k=1, …, K.
, k=1, …, K.
Шаг 3. Для распознаваемого объекта по тем же принципам и модальностям формируется модель G.
Шаг 4. Модель G сравнивается с каждой моделью  , k=1, …, K, в результате вычисляется множество отсчетов
, k=1, …, K, в результате вычисляется множество отсчетов  , характеризующих близость модели G к моделям
, характеризующих близость модели G к моделям  , k=1, …, K.
, k=1, …, K.
Шаг 5. Формируются множества 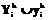 , k=1, …, K, которые принимаются за новые множества
, k=1, …, K, которые принимаются за новые множества  . Если множества
. Если множества  перестают изменяться, осуществляется переход к шагу 6 (могут использоваться и другие критерии перехода к шагу 6). В противном случае процедура начинается с шага 2.
перестают изменяться, осуществляется переход к шагу 6 (могут использоваться и другие критерии перехода к шагу 6). В противном случае процедура начинается с шага 2.
Шаг 6. Множества  объединяются, в результате получается множество
объединяются, в результате получается множество  , которое упорядочивается (если оно числовое, упорядочение осуществляется по возрастанию), а его элементы индексируются, i=1, ..., m, ji=0, ..., ni, в результате получается множество
, которое упорядочивается (если оно числовое, упорядочение осуществляется по возрастанию), а его элементы индексируются, i=1, ..., m, ji=0, ..., ni, в результате получается множество  i=1, ..., m, ji=0, ..., ni}. На множестве Yi задается функция принадлежности m(yij), yijÎYi, i=1, ..., m, j=0, ..., ni.
i=1, ..., m, ji=0, ..., ni}. На множестве Yi задается функция принадлежности m(yij), yijÎYi, i=1, ..., m, j=0, ..., ni.
Распознавание по любому отдельному алгоритму i с помощью функции  может осуществляться в соответствии со следующей процедурой 2.
может осуществляться в соответствии со следующей процедурой 2.
Шаг 0. С помощью процедуры 1 формируются множество Yi и функция принадлежности  i=0, ..., m, ji=0, ..., ni.
i=0, ..., m, ji=0, ..., ni.
Шаг 1. Для каждого эталонного объекта k, k=1, …, K, с помощью скрытых модальностей формируется своя эталонная модель  , k=1, …, K.
, k=1, …, K.
Шаг 2. Для распознаваемого объекта по тем же принципам и модальностям формируется модель G.
Шаг 3. Модель G сравнивается с каждой моделью  , k=1, …, K, в результате вычисляется множество отсчетов
, k=1, …, K, в результате вычисляется множество отсчетов  , характеризующих близость модели G соответственно к моделям
, характеризующих близость модели G соответственно к моделям  , k=1, …, K.
, k=1, …, K.
 Шаг 4. Модель G считается совпадающей с той эталонной моделью
Шаг 4. Модель G считается совпадающей с той эталонной моделью  , для которой значение
, для которой значение  , максимально.
, максимально.
Таким образом, функция принадлежности  , оценивает близость распознаваемой модели к соответствующей эталонной. В результате общий метод нечеткого агрегирования мультимодальной информации с помощью операторов Сугено или Шоке будет следующим.
, оценивает близость распознаваемой модели к соответствующей эталонной. В результате общий метод нечеткого агрегирования мультимодальной информации с помощью операторов Сугено или Шоке будет следующим.
Шаг 1. Для каждой модальности (сигнала) Yi, i=1, ..., m, выбрать значение g(Yi)Î[0, 1] как степень важности модальности Yi. Значения g(Yi) могут быть установлены экспертом, получены в результате наблюдений или каким-либо другим путем.
Шаг 2. Найти значение l, используя уравнение (5).
Шаг 3. Для распознаваемого объекта по каждому алгоритму i=1, …, m и для каждого k=1, …, K вычислить множество функций принадлежности  , i=1, …, m, с помощью процедуры 2.
, i=1, …, m, с помощью процедуры 2.
Шаг 4. Для каждого k=1, …, K упорядочить множество функций  таким образом, чтобы
таким образом, чтобы  .
.
Шаг 5. Для каждого k=1, …, K вычислить рекурсивно значения нечетких мер  , где
, где  , i=1, …, m, используя формулу (6).
, i=1, …, m, используя формулу (6).
Шаг 6. Вычислить для всех k=1, …, K значения операторов  (или
(или  ). Распознаваемый объект считается совпадающим с тем эталонным объектом, для которого значение
). Распознаваемый объект считается совпадающим с тем эталонным объектом, для которого значение  (или
(или  ) максимально.
) максимально.
Пример нечеткого агрегирования мультимодальной информации
Рассмотрим нечеткое агрегирование мультимодальной информации на примере распознавания пользователя по изображению верхней части его тела. Данный пример особенно актуален в интеллектуальных интерфейсах пользователя с современными компьютеризированными бытовыми приборами и биометрическими системами. Для распознавания пользователя используются три алгоритма: скрытая марковская модель (СММ), алгоритм определения цвета (АОЦ), алгоритм нахождения соотношений (АНС). Каждому алгоритму требуется обучение на всех пользователях, которых необходимо распознать. Для этого была заполнена БД, состоящая из записей знакомых пользователей. БД, хранящая необходимую информацию для алгоритмов распознавания, представлена на рисунке 1.
В алгоритме 1 используется модальность (множество отсчетов)  j1=0, ..., n1}. Используются эталонные СММ
j1=0, ..., n1}. Используются эталонные СММ  , k=1, …, K. Этим СММ соответствуют вероятности
, k=1, …, K. Этим СММ соответствуют вероятности  , k=1, …, K, распознавания с помощью этих моделей эталонных лиц, на которых происходило обучение моделей. Для вновь распознаваемого лица, используя те же модальности и модели
, k=1, …, K, распознавания с помощью этих моделей эталонных лиц, на которых происходило обучение моделей. Для вновь распознаваемого лица, используя те же модальности и модели  , k=1, …, K, вычисляются вероятности
, k=1, …, K, вычисляются вероятности  , k=1, …, K, его распознавания с помощью моделей
, k=1, …, K, его распознавания с помощью моделей  . Множество отсчетов
. Множество отсчетов  , k=1, …, K, вычисляется как разность вероятностей
, k=1, …, K, вычисляется как разность вероятностей  и
и  . На множестве
. На множестве  задается функция принадлежности
задается функция принадлежности  , j1=0, ..., n1. Ее график показан на рисунке 2а, из которого видно, что
, j1=0, ..., n1. Ее график показан на рисунке 2а, из которого видно, что  ={1/y10=0; 1/y11=1,5; 0/y12=2}.
={1/y10=0; 1/y11=1,5; 0/y12=2}.
В алгоритме 2 используется модальность 
 , j2=0, ..., n2, которая получается с помощью эталонных цветовых моделей
, j2=0, ..., n2, которая получается с помощью эталонных цветовых моделей  , k=1, …, K, в цветовом пространстве RGB. Здесь
, k=1, …, K, в цветовом пространстве RGB. Здесь  , j2=0, ..., n2, k=1, …, K – наборы эталонных значений красного, зеленого и синего цветов, на которых происходило обучение моделей,
, j2=0, ..., n2, k=1, …, K – наборы эталонных значений красного, зеленого и синего цветов, на которых происходило обучение моделей,  j2=0, ..., n2 – аналогичные наборы для вновь распознаваемого пользователя. На множестве Y2 задается функция принадлежности
j2=0, ..., n2 – аналогичные наборы для вновь распознаваемого пользователя. На множестве Y2 задается функция принадлежности 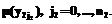 Ее график показан на рисунке 2б, из которого видно, что
Ее график показан на рисунке 2б, из которого видно, что 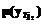 ={1/y20=0; 0,5/y21=20; 0/y22=40}.
={1/y20=0; 0,5/y21=20; 0/y22=40}.
В алгоритме 3 используется модальность (множество отсчетов) 
 j3=0, ..., n3}, которая получается с помощью эталонных моделей отношений
j3=0, ..., n3}, которая получается с помощью эталонных моделей отношений  , k=1, …, K. Здесь
, k=1, …, K. Здесь 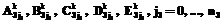 – наборы значений, соответственно, расстояний между глазами, глазами и носом, носом и ртом, глазами и ртом, глазами и подбородком, на которых происходило обучение моделей;
– наборы значений, соответственно, расстояний между глазами, глазами и носом, носом и ртом, глазами и ртом, глазами и подбородком, на которых происходило обучение моделей; 
 j3=0, …, n3 – аналогичные наборы для вновь распознаваемого лица. На множестве Y3 задается функция принадлежности
j3=0, …, n3 – аналогичные наборы для вновь распознаваемого лица. На множестве Y3 задается функция принадлежности  j3=0, …, n3. Ее график показан на рисунке 2в, из которого видно, что
j3=0, …, n3. Ее график показан на рисунке 2в, из которого видно, что  {1/y20=0; 0,5/y21=5; 0/y22=10}.
{1/y20=0; 0,5/y21=5; 0/y22=10}.
Продемонстрируем работу метода на примере рассмотренных модальностей и соответствующих им алгоритмов для одного распознаваемого объекта.
На первом шаге метода для каждой модальности Yi, i=1, …, m, выбираются значения степени важности g(Yi)Î[0, 1]. Экспертом в зависимости от силы алгоритма распознавания выбраны следующие значения: g(Y1)=0,9, g(Y2)=0,8, g(Y3)=0,4. Так как СММ имеет наиболее высокую надежность и устойчивость распознавания, для него задано самое большое значение степени важности. Эффективность решения задачи распознавания с помощью АОЦ несколько ниже, чем у первого алгоритма, поэтому его степень важности меньше. АНС является наиболее слабым из рассматриваемых алгоритмов, поэтому степень важности результатов распознавания этого алгоритма для общего результата агрегирования минимальная.
На втором шаге ищутся значения l, для чего фактически необходимо лишь решить уравнение (5) с полиномом степени (m-1) для нахождения корня, значение которого больше –1:


 (7)
(7)
Подставляя в (7) заданные g(Yi), получим:
0,288l2+1,4l+1,1=0. (8)
 Корнем данного уравнения является значение l= –0,989.
Корнем данного уравнения является значение l= –0,989.
На третьем шаге для распознаваемого объекта по каждому алгоритму i=1, …, 3 (в данном случае для одного k=1) вычисляется множество функций принадлежности  . Предположим, что получены следующие значения функций принадлежности: m(y1)=0,9, m(y2)=0,9, m(y3)=0,1.
. Предположим, что получены следующие значения функций принадлежности: m(y1)=0,9, m(y2)=0,9, m(y3)=0,1.
На четвертом шаге для каждого k=1, …, K упорядочивается множество функций  таким образом, чтобы
таким образом, чтобы  , jnÎ{1, …, m}. В рассматриваемом примере значения функций принадлежности уже упорядочены: m(y1)=0,9³m(y2)=0,9³m(y3)=0,1.
, jnÎ{1, …, m}. В рассматриваемом примере значения функций принадлежности уже упорядочены: m(y1)=0,9³m(y2)=0,9³m(y3)=0,1.
На пятом шаге с использованием формулы (6) для каждого k=1, …, K вычисляются значения нечетких мер  , где
, где  i=1, …, m:
i=1, …, m:
g(Q1)=g(Y1)=0,9;
g(Q2)=0,8+0,9–0,989×0,8×0,9=0,98;
g(Q3)=0,4+0,98–0,989×0,4×0,98=1. (9)
На заключительном шаге метода для всех k=1, …, K вычисляются значения операторов  или
или  по формулам (3) и (4):
по формулам (3) и (4):
AC=max[min(0,9, 0,9), min(0,9, 0,98),
min(0,1, 1))]=max[0,9, 0,9, 0,1]=0,9; (10)
AШ=(0,9–0,9)×0,9+(0,9–0,1)×0,98+(0,1–0)×1=0,88.
Подытоживая, отметим, что рассмотрен метод нечеткого агрегирования мультимодальной информации с использованием операторов агрегирования (операторов Сугено или Шоке).
Главные достоинства и отличия предлагаемого метода от известных аналогов следующие. Учет степени важности каждой модальности и их отношений происходит непосредственно в процессе распознавания за счет применения операторов агрегирования, использующих нечеткую меру. Надежность распознавания отдельных объектов (например внешности пользователя) повышается за счет использования нескольких источников информации. Кроме того, с помощью данного метода создаются основы для разработки систем управления различными объектами (роботами, компьютерами, телевизорами и т.п.) и открываются пути повышения интеллектуальности и интуитивности человеко-машинных интерфейсов за счет использования широкого спектра модальностей и их отношений.
Литература
1. Sharma R. Speech-Gesture Driven Multimodal Interfaces for Crisis Management // The IEEE Proceedings. 2003. Vol. 91, № 9, pp. 1327–1354.
2. Ронжин А.Л., Карпов А.А., Ли И.В. Речевой и многомодальный интерфейсы. М.: Наука, 2006. 172 с.
3. Akasaka Y., Onisawa T. Individualized pedestrian navigation using fuzzy measures and integrals // Proc of IEEE Intern. Conf. on syst., man and cybern. Hawai, 2005. Vol. 2, pp. 1461–1466.
4. Tahani H., Keller J.M. Information fusion in computer vision using the Fuzzy integral // IEEE transactions on systems, man and cybernetics. 1990. Vol. 20, № 3, pp. 733–741.
5. Kwak K., Pedrycz W. Face recognition: A study in information fusion using fuzzy integral // Patt. Recog. Lett. 2005. Vol. 26, pp. 719–733.
 , (1)
, (1) языка распознаваемого жеста различным нечетким языкам эталонных жестов как максимум из всех значений этих функций (в данном случае kÎ{1, …, K}, K – число распознаваемых объектов). Обычно подобные агрегирующие функции Ak называют операторами агрегирования. Оператор агрегирования (1) назовем max-оператором. Использование max-оператора для распознавания модальностей обеспечивает высокий уровень надежности, но может быть неэффективным для использования на верхнем уровне.
языка распознаваемого жеста различным нечетким языкам эталонных жестов как максимум из всех значений этих функций (в данном случае kÎ{1, …, K}, K – число распознаваемых объектов). Обычно подобные агрегирующие функции Ak называют операторами агрегирования. Оператор агрегирования (1) назовем max-оператором. Использование max-оператора для распознавания модальностей обеспечивает высокий уровень надежности, но может быть неэффективным для использования на верхнем уровне. , (2)
, (2) .
. , (3)
, (3) Qi={Y1, …, Yi}, i=1, …, m.
Qi={Y1, …, Yi}, i=1, …, m.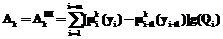 , (4)
, (4)
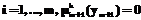 .
. . (5)
. (5) .
.
 , i=0, ..., m, ji=0, ..., ni. Задачей является агрегирование модальностей Yi, i=0, ..., m. Для того чтобы сформировать множество Yi и функции принадлежности
, i=0, ..., m, ji=0, ..., ni. Задачей является агрегирование модальностей Yi, i=0, ..., m. Для того чтобы сформировать множество Yi и функции принадлежности  i=0, ..., m, ji=0, ..., ni, каждый алгоритм проходит предварительную обработку в соответствии со следующей процедурой 1.
i=0, ..., m, ji=0, ..., ni, каждый алгоритм проходит предварительную обработку в соответствии со следующей процедурой 1. , k=1, …, K.
, k=1, …, K. , k=1, …, K.
, k=1, …, K. , характеризующих близость модели G к моделям
, характеризующих близость модели G к моделям 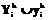 , k=1, …, K, которые принимаются за новые множества
, k=1, …, K, которые принимаются за новые множества  . Если множества
. Если множества  , которое упорядочивается (если оно числовое, упорядочение осуществляется по возрастанию), а его элементы индексируются, i=1, ..., m, ji=0, ..., ni, в результате получается множество
, которое упорядочивается (если оно числовое, упорядочение осуществляется по возрастанию), а его элементы индексируются, i=1, ..., m, ji=0, ..., ni, в результате получается множество  i=1, ..., m, ji=0, ..., ni}. На множестве Yi задается функция принадлежности m(yij), yijÎYi, i=1, ..., m, j=0, ..., ni.
i=1, ..., m, ji=0, ..., ni}. На множестве Yi задается функция принадлежности m(yij), yijÎYi, i=1, ..., m, j=0, ..., ni. может осуществляться в соответствии со следующей процедурой 2.
может осуществляться в соответствии со следующей процедурой 2. i=0, ..., m, ji=0, ..., ni.
i=0, ..., m, ji=0, ..., ni. , k=1, …, K.
, k=1, …, K. , характеризующих близость модели G соответственно к моделям
, характеризующих близость модели G соответственно к моделям  Шаг 4. Модель G считается совпадающей с той эталонной моделью
Шаг 4. Модель G считается совпадающей с той эталонной моделью  , максимально.
, максимально. , i=1, …, m, с помощью процедуры 2.
, i=1, …, m, с помощью процедуры 2. таким образом, чтобы
таким образом, чтобы  .
. , где
, где  , i=1, …, m, используя формулу (6).
, i=1, …, m, используя формулу (6). (или
(или  ). Распознаваемый объект считается совпадающим с тем эталонным объектом, для которого значение
). Распознаваемый объект считается совпадающим с тем эталонным объектом, для которого значение  ) максимально.
) максимально. j1=0, ..., n1}. Используются эталонные СММ
j1=0, ..., n1}. Используются эталонные СММ  , k=1, …, K. Этим СММ соответствуют вероятности
, k=1, …, K. Этим СММ соответствуют вероятности  , k=1, …, K, распознавания с помощью этих моделей эталонных лиц, на которых происходило обучение моделей. Для вновь распознаваемого лица, используя те же модальности и модели
, k=1, …, K, распознавания с помощью этих моделей эталонных лиц, на которых происходило обучение моделей. Для вновь распознаваемого лица, используя те же модальности и модели  , k=1, …, K, вычисляются вероятности
, k=1, …, K, вычисляются вероятности  , k=1, …, K, его распознавания с помощью моделей
, k=1, …, K, его распознавания с помощью моделей  , k=1, …, K, вычисляется как разность вероятностей
, k=1, …, K, вычисляется как разность вероятностей  задается функция принадлежности
задается функция принадлежности  , j1=0, ..., n1. Ее график показан на рисунке 2а, из которого видно, что
, j1=0, ..., n1. Ее график показан на рисунке 2а, из которого видно, что  ={1/y10=0; 1/y11=1,5; 0/y12=2}.
={1/y10=0; 1/y11=1,5; 0/y12=2}.
 , j2=0, ..., n2, которая получается с помощью эталонных цветовых моделей
, j2=0, ..., n2, которая получается с помощью эталонных цветовых моделей  , k=1, …, K, в цветовом пространстве RGB. Здесь
, k=1, …, K, в цветовом пространстве RGB. Здесь  , j2=0, ..., n2, k=1, …, K – наборы эталонных значений красного, зеленого и синего цветов, на которых происходило обучение моделей,
, j2=0, ..., n2, k=1, …, K – наборы эталонных значений красного, зеленого и синего цветов, на которых происходило обучение моделей,  j2=0, ..., n2 – аналогичные наборы для вновь распознаваемого пользователя. На множестве Y2 задается функция принадлежности
j2=0, ..., n2 – аналогичные наборы для вновь распознаваемого пользователя. На множестве Y2 задается функция принадлежности 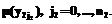 Ее график показан на рисунке 2б, из которого видно, что
Ее график показан на рисунке 2б, из которого видно, что 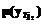 ={1/y20=0; 0,5/y21=20; 0/y22=40}.
={1/y20=0; 0,5/y21=20; 0/y22=40}.
 j3=0, ..., n3}, которая получается с помощью эталонных моделей отношений
j3=0, ..., n3}, которая получается с помощью эталонных моделей отношений  , k=1, …, K. Здесь
, k=1, …, K. Здесь 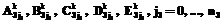 – наборы значений, соответственно, расстояний между глазами, глазами и носом, носом и ртом, глазами и ртом, глазами и подбородком, на которых происходило обучение моделей;
– наборы значений, соответственно, расстояний между глазами, глазами и носом, носом и ртом, глазами и ртом, глазами и подбородком, на которых происходило обучение моделей; 
 j3=0, …, n3 – аналогичные наборы для вновь распознаваемого лица. На множестве Y3 задается функция принадлежности
j3=0, …, n3 – аналогичные наборы для вновь распознаваемого лица. На множестве Y3 задается функция принадлежности  j3=0, …, n3. Ее график показан на рисунке 2в, из которого видно, что
j3=0, …, n3. Ее график показан на рисунке 2в, из которого видно, что  {1/y20=0; 0,5/y21=5; 0/y22=10}.
{1/y20=0; 0,5/y21=5; 0/y22=10}.

 (7)
(7)
 . Предположим, что получены следующие значения функций принадлежности: m(y1)=0,9, m(y2)=0,9, m(y3)=0,1.
. Предположим, что получены следующие значения функций принадлежности: m(y1)=0,9, m(y2)=0,9, m(y3)=0,1. , jnÎ{1, …, m}. В рассматриваемом примере значения функций принадлежности уже упорядочены: m(y1)=0,9³m(y2)=0,9³m(y3)=0,1.
, jnÎ{1, …, m}. В рассматриваемом примере значения функций принадлежности уже упорядочены: m(y1)=0,9³m(y2)=0,9³m(y3)=0,1. , где
, где  i=1, …, m:
i=1, …, m: по формулам (3) и (4):
по формулам (3) и (4):