Journal influence
Bookmark
Next issue
Method for parameter estimation of nonlinear kinetic models of multistage chemical reactions
The article was published in issue no. № 4, 2011 [ pp. 163 – 168 ]Abstract:The basic stages of carrying out of kinetic studies, construction of high-precision kinetic models, and identification of kinetic constants of models, planning of starting and precision experiments are considered. A set of algorithms and programs for identification of kinetic constants of complex chemical reactions, planning of precision experiments and construction of optimal plans of experiments according to the criterion of a D-optimality has been developed.
Аннотация:Рассмотрены основные этапы проведения кинетических исследований, построения высокоточных кинетических моделей, идентификации констант моделей, планирования стартовых и прецизионных экспериментов. Разработаны комплексы алгоритмов и программ идентификации констант кинетических моделей сложных химических реакций, планирования прецизионных экспериментов и построения оптимальных планов экспериментов по критерию D-оптимальности.
| Authors: (evpisarenko@mail.ru) - , Ph.D | |
| Keywords: experimental planning, constant identification, chemical kinetics |
|
| Page views: 9438 |
Print version Full issue in PDF (5.83Mb) Download the cover in PDF (1.28Мб) |
Рост цен на энергоносители требует разработки новых технологий производств, которые позволяют использовать как целевые продуктовые потоки, так и все многообразие побочных продуктов [1]. Следовательно, необходимы кинетические модели, с помощью которых можно с высокой точностью рассчитать концентрацию всех этих продуктов. Для построения подобных моделей необходимо учитывать протекание в химической системе большого количества элементарных химических реакций. Значение и роль кинетических исследований [2] в общей процедуре моделирования химического процесса исключительно велики, поскольку необоснованно выбранная неполная система гипотез о механизме реакции не может привести к установлению кинетических моделей, правильно отражающих структуру химических превращений и позволяющих с высокой степенью надежности прогнозировать статические и динамические свойства изучаемой химической системы. Из теоремы эквивалентности [3] известно, что построение высокоточных кинетических моделей, то есть моделей, чрезвычайно точно прогнозирующих изменение в ходе реакции основных показателей химического процесса, невозможно без оценки по экспериментальным данным высокоточных кинетических констант. Последнее достигается планированием кинетического эксперимента с целью получения при каждом опыте мак- симальной информации о численных значениях кинетических констант. Проблема построения кинетической модели сложной химической реакции и оценки кинетических констант модели решается по следующей схеме. · Формирование возможного механизма протекания многомаршрутной химической реакции, оценка числа маршрутов, векторов стехиометрических чисел маршрутов и возможных итоговых уравнений маршрутов. · Формирование алгоритмов построения кинетических моделей анализируемой реакционной системы, не противоречащих теории реакционноспособности химических соединений и основным положениям химической кинетики. · Построение кинетических моделей изучаемой химической реакции. · Планирование стартовых кинетических экспериментов. · Качественный анализ кинетических моделей протекания реакции и оценки свойств решений уравнений кинетических моделей. · Оценка идентифицируемости кинетических констант моделей при условии протекания химической реакции в квазистационарных условиях по промежуточным веществам и в заданной области проведения кинетического эксперимента. · Планирование прецизионных экспериментов с целью получения оценок кинетических констант моделей с точностью, обеспечивающей заданные априори прогнозирующие возможности кинетической модели. · Проверка соответствия построенного прецизионного плана эксперимента критерию D-оптимальности [4]. · Построение доверительных областей для векторов кинетических констант и откликов модели, подтверждающих необходимую для последующего моделирования режимов работы реактора высокую точность расчета по кинетической модели основных показателей химического процесса. Для возможности использования персональных компьютеров при анализе химических реагирующих систем химические реагенты и хими- ческие реакции отображаются в векторы
B×A=0, (2) где При условиях квазистационарного протекания химической реакции часть реагентов (боденштейновские вещества) имеют значение скоростей Следовательно, процедура построения кинетической модели химической реакции и оценки ее кинетических констант выполняется в следующей последовательности. 1. Матрица B представляется в виде клеточной матрицы B=[Bн½Bб]. 2. Определяется ранг матрицы Bб, и в соответствии с правилом Хориути рассчитывается количество независимых маршрутов реакции P, где P=Q–rank(Вб), и количество уравнений L1 химических инвариантов для боденштейновских веществ, где L1=(N–L) –rank(Bб). 3. Определяются уравнения химических инвариантов для боденштейновских веществ. Имеем
где Bб=[Bб1½B2б2] и 4. Рассчитываются Р векторов стехиометрии- ческих чисел маршрутов 5. Рассчитываются компоненты транспонированной матрицы стехиометрических коэффициентов итоговых реакций по маршрутам 6. Определяется ранг матрицы итоговых уравнений Bu по маршрутам. Матрица Bu представляется в виде клеточной матрицы Bu=[Bu1½Bu2], где rank(Bu)=rank(Bu1). По неособенной квадратной подматрице Bu1 устанавливаются ключевые вещества, а по подматрице Bu2 независимые. Определяются уравнения химических инвариантов для неключевых (независимых) веществ. Последние имеют вид
где Если в итоговых уравнениях маршрутов не все химические реакции независимые, число ненулевых строк подматрицы Bu1 будет меньше числа строк матрицы Bu. При этом вид уравнений (4) сохраняется. 7. По матричному соотношению рассчитываются компоненты вектора скоростей по маршрутам
где Следовательно, для различных векторов стехиометрических чисел 8. Проводится стартовый эксперимент, и методом наименьших квадратов или максимального правдоподобия вычисляются предварительные оценки кинетических констант. 9. Определяется количество констант (или их комбинаций), допускающих оценку. Для решения этой задачи вычисляется детерминант информационной матрицы многооткликовой модели detM(e) или его миноры в точках плана ε в выбранной области экспериментирования G, то есть
где m – число откликов модели, по значениям которых оцениваются кинетические константы; N1 – число кинетических экспериментов; n – число кинетических констант в модели; S – дисперсионно-ковариационная матрица наблюдений; Очевидно, что detM(e)¹0 только при условии, что N´m³n, ибо матрица M(e) неособенная только при условии, что число ее независимых строк и/или столбцов равно n. Вычисляется ненулевой минор M1 наибольшего порядка информационной матрицы M(e). При этом максимальное число параметров (или их комбинаций), допускающих оценку, определяется порядком подматрицы M1. 10. Строится плотность распределения detM1(e), и проверяется гипотеза о том, что определитель выбранной подматрицы M1 статистически значимо отличается от нуля. Если это утверждение верно, по вычисленному минору устанавливаются константы модели (или их комбинации), допускающие оценку. Определим их как независимые константы. 11. Переоцениваются константы кинетической модели, уже как комплексы констант, методом наименьших квадратов. Решение дифференциальных уравнений модели осуществляется полунеявным методом Рунге–Кутта III порядка. Мини- мизация функционала, характеризующего соответ- ствие модели эксперименту, осуществляется методами Маркуардта, Ньютона, Хука–Дживса, случайного поиска. Оценки независимых констант будут определяться как результатами эксперимента, так и задаваемыми численными значениями остальных зависимых констант. В качестве зависимых констант целесообразно выбирать такие константы, объем априорной информации о которых максимален. Очевидно, что численные значения, присваиваемые зависимым константам, не могут повлиять на предсказательную силу математической модели. Мощность множества допускающих оценку констант определяется, в свою очередь, свойствами плана эксперимента. Она максимальна для оптимального плана, так как число констант со статистически значимой параметрической чувствительностью максимально. При этом для нелинейных моделей ранг матрицы M(e) и результаты анализа на параметрическую чувствительность констант зависят от численных значений констант, и, следовательно, процедура исследования максимально возможного числа оцениваемых констант должна проводиться на всех этапах последовательного прецизионного уточнения параметров. В кинетической модели вследствие использования условий квазистационарности по боденштейновским веществам возможно возникновение ситуаций, когда определенные совокупности констант не могут быть определены индивидуально и оцениваются только в виде некоторых функциональных соотношений (комбинаций линейных и нелинейных). Такова структура кинетической модели, и никакое планирование эксперимента не может исправить это положение. В модели существуют и константы (или комбинации констант) с низкой параметрической чувствительностью, которые при данном плане эксперимента не могут быть оценены с приемлемой точностью. Например, константы характеризуют химическую реакцию, которая в исследуемой области практически не протекает, но с заметной скоростью идет в другой. Поэтому в качестве критерия планирования эксперимента требуется использовать и комбинированный критерий, который предусматривает максимизацию как ранга информационной матрицы плана, так и его детерминанта. 12. Точность прогноза по модели определяется дисперсионно-ковариационной матрицей
где
После каждого эксперимента необходимо осуществлять проверку точности проведенных расчетов элементов информационной матрицы плана M(e) и элементов дисперсионно-ковариационной матрицы прогноза по модели
где Последовательное непрерывное планирование, от опыта к опыту максимизирующее detM(e), приводит к построению D-оптимального плана эксперимента, если выполняется условие
Это условие по теореме эквивалентности для многооткликовых моделей эквивалентно условию
где e* – D-оптимальный план эксперимента. После построения D-оптимального плана эксперимента переходят к последовательному планированию эксперимента по максимизации ранга информационной матрицы M(e). По завершении этого этапа, при достижении увеличения ранга M(e), снова переходят к планированию прецизионного эксперимента по этапам, изложенным выше. Если при проведении уточняющего прецизионного эксперимента сходимость к оптимальному плану эксперимента невысока и прогнозирующая способность модели не удовлетворяет априори заданным требованиям, то после выбора нового вектора констант, допускающих оценку, необходимо вернуться к этапам 1–12. При новых предположениях по результатам ранее проведенных экспериментов оцениваются отдельные константы модели или их комбинации. Определяется параметрическая чувствительность констант, и формируется новая информационная матрица M(e). Устанавливаются ее ранг и детерминант. Далее вновь проводится последовательное планирование уточняющих экспериментов с целью получения кинетической модели с заданными свойствами. Указанная выше процедура построения кинетических моделей прошла апробацию при построении кинетических моделей многомаршрутных реакций паровой конверсии метанола и конверсии смеси метанола и диметилового эфира в олефиновые углеводороды [5] и показала себя достаточно продуктивной. Экспериментальные исследования кинетики реакции конверсии метанола и диметилового эфира в низшие олефины проводились в проточно-циркуляционном реакторе с внутренним контуром циркуляции. Реактор позволяет проводить экспериментальные исследования в диапазоне температур 350–600 оС и давлений от 0,1 МПа до 6,0 МПа. В реактор загружался мелкодисперсный высококремнистый цеолитный катализатор объемом 5–50 мл. Предложен 25-стадийный механизм реакции конверсии метанола и диметилового эфира в олефиновые углеводороды. Построена кинетическая модель анализируемой реакционной системы. Поскольку в моделях не все кинетические константы можно оценить по экспериментальным данным, при постановке эксперимента и обработке его результатов требовалось установить число индивидуальных констант или их комплексов, допускающих оценку. Точность оцененных констант определяется по детерминанту дисперсионно-ковариационной матрицы оценок констант. Чем меньше детерминант, тем точнее оценки кинетических констант модели. Сущность нового метода заключается не только в определении числа констант, допускающих оценку, но и в планировании эксперимента таким образом, чтобы оценить максимальное количество кинетических констант. В противном случае кинетическая модель не будет прогнозировать результаты эксперимента с высокой точностью. По результатам эксперимента в выбранной области экспериментирования были установлены численные значения кинетических констант и их комбинаций модели реакции получения олефи- новых углеводородов, допускающих оценку. С использованием построенной плотности распределения DetM(e) выделена критическая область значений, в которой DetM(e) статистически незначимо отличаются от нуля. Для оценки параметров кинетической модели пригодны лишь те значения DetM(e), которые не принадлежат критической области. В рассматриваемом случае из кинетической модели выделены 18 независимых комбинаций констант, которые определяет невырожденная информационная матрица плана. Следовательно, выбранные 18 комбинаций кинетических констант могут быть оценены по результатам кинетического эксперимента. Таким образом, вследствие того, что химические реакции в реакторах протекают обычно в квазистационарном режиме, система кинетических уравнений распадается на две подсистемы – систему дифференциальных уравнений и систему алгебраических уравнений. Каждое из последних уравнений равно нулю при любом значении независимой переменной (время, длина реактора и т.п.), поэтому существуют функциональные соотношения между кинетическими константами. Причем число функциональных соотношений меньше числа кинетических констант. Следовательно, в области квазистационарного протекания реакции определить численные значения всех кинетических констант принципиально невозможно. Возникает проблема, какие кинетические константы или их комбинации можно определить по экспериментальным данным и при каких условиях проведения эксперимента константы (или их комбинации) будут оценены с наибольшей точностью для заданного объема эксперимента. На решение подобных проблем направлен изложенный выше метод оценки констант нелинейных кинетических моделей многостадийных многомаршрутных химических реакций и разработанный пакет прикладных программ «KINCON_IDENTIFICATION» на Compaq Visual Fortran 6.6 и С++. Он дает возможность установить область проведения химической реакции, в которой допускается оценка максимального числа кинетических констант (или их комбинаций); для заданного объема эксперимента оценить кинетические константы с максимально возможной точностью (для D-оптимального плана эксперимента); построить кинетическую модель с высокой прогнозирующей возможностью. Предложенные методы и программы прошли проверку при решении многих практических задач. Литература 1. Chul-Jin Lee [et al.]. Optimal gas-to-liquid selection from natural gas under uncertain price scenarios // Ind. Eng. Chem. Res., 2009. Vol. 48, pp. 794–800. 2. Wojciechowsky B.W. and Rice R.M. Experimental methods in kinetic studies // Elsevier Science B.V. Amsterdam, Netherlands, 2003. 3. Федоров В.В. Теория оптимального эксперимента. М.: Наука, 1971. 312 с. 4. Berding C., Kleider W. and Gössl R. D-optimal planning & experimentation the tool for experimental design in research and development // Computational Statistics & Data Analysis, 1996. Vol. 21. Is. 6, pp. 705–710. 5. Писаренко Е.В., Писаренко В.Н. Кинетика реакции синтеза олефинов на основе метанола и диметилового эфира // Теоретические основы химической технологии, 2008. Т. 42. № 6. С. 623–632. |
| Permanent link: http://swsys.ru/index.php?id=2939&lang=en&page=article |
Print version Full issue in PDF (5.83Mb) Download the cover in PDF (1.28Мб) |
| The article was published in issue no. № 4, 2011 [ pp. 163 – 168 ] |
Back to the list of articles
 ,
,  различной размерности, компоненты которых – целые или рациональные числа. Совокупность векторов
различной размерности, компоненты которых – целые или рациональные числа. Совокупность векторов 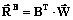 , (1)
, (1) – вектор скоростей изменения концентраций реагентов;
– вектор скоростей изменения концентраций реагентов;  – вектор скоростей элементарных каталитических и некаталитических химических реакций.
– вектор скоростей элементарных каталитических и некаталитических химических реакций. , L+1£k£N, другая часть реагентов (небоденштейновские вещества) имеют значения величин скоростей
, L+1£k£N, другая часть реагентов (небоденштейновские вещества) имеют значения величин скоростей  , 1£m£L. В соответствии с вышеизложенным матрица B представима в виде двух подматриц: Bн – подматрица стехиометрических коэффициентов небоденштейновских веществ; Bб – подматрица стехиометрических коэффициентов боденштейновских веществ. Таким образом, имеем B=[Bн½Bб].
, 1£m£L. В соответствии с вышеизложенным матрица B представима в виде двух подматриц: Bн – подматрица стехиометрических коэффициентов небоденштейновских веществ; Bб – подматрица стехиометрических коэффициентов боденштейновских веществ. Таким образом, имеем B=[Bн½Bб]. , (3)
, (3) – неособенная квадратная подматрица стехиометрической матрицы Bб ранга rank(Bб1)=rank(Bб)=s;
– неособенная квадратная подматрица стехиометрической матрицы Bб ранга rank(Bб1)=rank(Bб)=s; ,
, 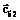 – подвекторы вектора концентраций боденштейновских веществ; t – независимая переменная, время, длина реактора и т.п.
– подвекторы вектора концентраций боденштейновских веществ; t – независимая переменная, время, длина реактора и т.п. , 1£p£P, решением системы линейных однородных уравнений, соответствующей матричному уравнению
, 1£p£P, решением системы линейных однородных уравнений, соответствующей матричному уравнению  . Расчет независимых векторов стехиометрических чисел
. Расчет независимых векторов стехиометрических чисел  неоднозначен в том смысле, что их число всегда Р, но компоненты векторов могут быть различны, ибо размерность матрицы
неоднозначен в том смысле, что их число всегда Р, но компоненты векторов могут быть различны, ибо размерность матрицы  есть (N–L)´Q, причем (N–L) – рациональные числа, общее количество решений счетно. Среди них выбираем только линейно независимые решения, тривиальное решение не рассматривается, так как ему соответствует отсутствие химических реакций в анализируемой системе. Каждое независимое решение определяет со- вокупность стехиометрических чисел стехио- метрического вектора, которому соответствует определенное выражение итоговой реакции по маршруту.
есть (N–L)´Q, причем (N–L) – рациональные числа, общее количество решений счетно. Среди них выбираем только линейно независимые решения, тривиальное решение не рассматривается, так как ему соответствует отсутствие химических реакций в анализируемой системе. Каждое независимое решение определяет со- вокупность стехиометрических чисел стехио- метрического вектора, которому соответствует определенное выражение итоговой реакции по маршруту. , причем в зависимости от выбранных компонентов P векторов стехиометрических чисел (матрица v) получаются различные итоговые уравнения реакций по маршрутам.
, причем в зависимости от выбранных компонентов P векторов стехиометрических чисел (матрица v) получаются различные итоговые уравнения реакций по маршрутам. , (4)
, (4) ,
,  – векторы концентраций независимых и ключевых веществ соответственно;
– векторы концентраций независимых и ключевых веществ соответственно;  ,
,  – векторы начальных значений концентраций независимых и ключевых веществ соответственно.
– векторы начальных значений концентраций независимых и ключевых веществ соответственно. , 1£p£P, и компоненты вектора концентраций боденштейновских веществ как функции концентраций небоденштейновских веществ и кинетических констант:
, 1£p£P, и компоненты вектора концентраций боденштейновских веществ как функции концентраций небоденштейновских веществ и кинетических констант: , (5)
, (5) – вектор скоростей по маршрутам.
– вектор скоростей по маршрутам. . Так как кинетические модели построены для условий квазистационарности по промежуточным веществам и при этом как объем эксперимента, так и область экспериментирования ограничены, не все индивидуальные кинетичес- кие константы допускают оценку, часть из них или даже все константы оцениваются в виде определенных линейных или нелинейных соотношений.
. Так как кинетические модели построены для условий квазистационарности по промежуточным веществам и при этом как объем эксперимента, так и область экспериментирования ограничены, не все индивидуальные кинетичес- кие константы допускают оценку, часть из них или даже все константы оцениваются в виде определенных линейных или нелинейных соотношений.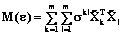 . (6)
. (6) , 1£l£m, (7)
, 1£l£m, (7) , 1£i£N1, 1£f£n, (8)
, 1£i£N1, 1£f£n, (8) , 1£s£m, 1£q£m, (9)
, 1£s£m, 1£q£m, (9) – условия проведения i-го эксперимента.
– условия проведения i-го эксперимента. откликов
откликов 
 вида
вида , (10)
, (10) – условия проведения эксперимента в области экспериментирования G;
– условия проведения эксперимента в области экспериментирования G;  – вектор кинетических констант; e – план эксперимента;
– вектор кинетических констант; e – план эксперимента;  – значение концентрации i-го реагента в точке
– значение концентрации i-го реагента в точке  =M(e):
=M(e): . (11)
. (11) по матричному уравнению
по матричному уравнению , (12)
, (12) , 1£u£N – точка спектра плана; pu, 1£u£N – веса плана; S – дисперсионно-ковариационная матрица наблюдений в точке
, 1£u£N – точка спектра плана; pu, 1£u£N – веса плана; S – дисперсионно-ковариационная матрица наблюдений в точке  – след матрицы
– след матрицы  .
. . (13)
. (13) , (14)
, (14)